D. Tree Construction time limit per test 2 seconds memory limit per test 256 megabytes input standard input output standard output

During the programming classes Vasya was assigned a difficult problem. However, he doesn't know how to code and was unable to find the solution in the Internet, so he asks you to help.

You are given a sequence a, consisting of n distinct integers, that is used to construct the binary search tree. Below is the formal description of the construction process.

1. First element a1 becomes the root of the tree.
2. Elements a2, a3, ..., an are added one by one. To add element ai one needs to traverse the tree starting from the root and using the following rules:
   1. The pointer to the current node is set to the root.
   2. If ai is greater than the value in the current node, then its right child becomes the current node. Otherwise, the left child of the current node becomes the new current node.
   3. If at some point there is no required child, the new node is created, it is assigned value ai and becomes the corresponding child of the current node.

Input

The first line of the input contains a single integer n (2 ≤ n ≤ 100 000) — the length of the sequence a.

The second line contains n distinct integers a

i (1 ≤ ai ≤ 109) — the sequence a itself.

Output

Output n - 1 integers. For all i > 1 print the value written in the node that is the parent of the node with value ai in it.

Examples input

3
1 2 3

output

1 2

input

5
4 2 3 1 6

output

4 2 2 4

Note

Picture below represents the tree obtained in the first sample.

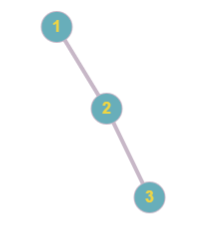
Picture below represents the tree obtained in the second sample.

題目大意：建立二叉查詢樹。新增n個結點，輸出新增第2~n個結點時 對應的父節點值(第1個點是根 無父節點 故不輸出

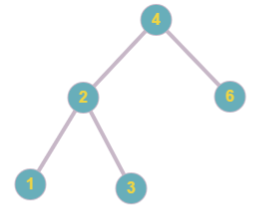
首先要找到一個結論:對於已新增第1~(i-1)個結點的樹，新增第i個結點v時，父親一定是之前新增的值最接近v的點。即min(|u-v|)的那個u

這樣會出現u < v或者u > v（及左邊最靠近v和右邊最靠近v的）兩種 一定是選擇最晚出現的u來作為v的父親。

因為對於兩個u此時已經加入到樹中，而且在沒有v之前，uL與uR是相鄰(連)的。及其中一個為另一個父親

其實也就是較早出現的為較晚出現的那個點的父親。

線上處理的話，如果能很快插入的話，保證序列有序，每次插入一個點前，二分出該點的左右鄰點，找出其中最晚出現的，即為該點父親。

我用的vector超時了，看他們有用set過的。。。沒試

後來想到禿頭，想出一個離線處理的方法。

先把所有點存下來，並按點值從小到大排序，然後去個重。同時，每個點記錄最早出現的時刻，還有左右鄰點。

然後從第n次加入到第2次加入的點遍歷(讀取的時候預先備份一下即可

二分找到這個點，然後比較下左右鄰點，選取所需要的即可。

如果找某個點時，發現再往前沒有該點，把他左右鄰點連結即可。即為將該點扣去。

程式碼如下:

#include <bits/stdc++.h>
#define LL long long

using namespace std;
const int INF = 0x3f3f3f3f;
const int mod = 1e9+7;
const double eps = 1e-8;

struct Node
{
    int x,mn,mx,l,r;
    bool operator < (const struct Node a)const
    {
        return x < a.x;
    }
};

Node nd[100100];
int x[100100];
int ans[100100];
int tp = 0;

int main()
{
    int n,l,r,pos;

    scanf("%d",&n);

    for(int i = 0; i < n; ++i)
    {
        scanf("%d",&x[i]);
<span style="white-space:pre">	</span>nd[i].x = x[i];
        nd[i].mn = nd[i].mx = i;
    }

    sort(nd,nd+n);

    for(int i = 0; i < n; ++i)
    {
        if(tp == 0 || nd[i].x != nd[tp-1].x)
        {
            nd[tp++] = nd[i];
            nd[tp-1].l = tp-2;
            nd[tp-1].r = tp;
        }
        else
        {
            nd[tp-1].mn = min(nd[tp-1].mn,nd[i].mn);
            nd[tp-1].mx = min(nd[tp-1].mn,nd[i].mx);
        }
    }

    for(int i = n-1; i > 0; --i)
    {
        l = 0, r = tp-1;

        while(l <= r)
        {
            int mid = (l+r)>>1;
            if(nd[mid].x == x[i])
            {
                pos = mid;
                break;
            }
            else if(nd[mid].x > x[i]) r = mid-1;
            else l = mid+1;
        }

        if(nd[pos].l == -1) ans[i] = nd[nd[pos].r].x;
        else if(nd[pos].r == tp) ans[i] = nd[nd[pos].l].x;
        else if(nd[nd[pos].r].mn > nd[nd[pos].l].mn) ans[i] = nd[nd[pos].r].x;
        else ans[i] = nd[nd[pos].l].x;

        if(nd[pos].mn == i)
        {
            nd[nd[pos].l].r = nd[pos].r;
            nd[nd[pos].r].l = nd[pos].l;
        }
    }

    for(int i = 1; i < n; ++i)
    {
        if(i != 1) putchar(' ');
        printf("%d",ans[i]);
    }

    return 0;
}