JAVA: 整數中1出現的次數(從1到n整數中1出現的次數)(變型:整數中k出現的次數)
阿新 • • 發佈:2019-01-25
題目:求出1~13的整數中1出現的次數,並算出100~1300的整數中1出現的次數?為此他特別數了一下1~13中包含1的數字有1、10、11、12、13因此共出現6次,但是對於後面問題他就沒轍了。ACMer希望你們幫幫他,並把問題更加普遍化,可以很快的求出任意非負整數區間中1出現的次數。
分析:
考慮將n的十進位制的每一位單獨拿出討論,每一位的值記為weight。
1) 個位
從1到n,每增加1,weight就會加1,當weight加到9時,再加1又會回到0重新開始。那麼weight從0-9的這種週期會出現多少次呢?這取決於n的高位是多少,看圖:
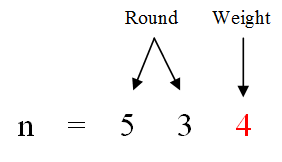
以534為例,在從1增長到n的過程中,534的個位從0-9變化了53次,記為round。每一輪變化中,1在個位出現一次,所以一共出現了53次。
再來看weight的值。weight為4,大於0,說明第54輪變化是從0-4,1又出現了1次。我們記1出現的次數為count,所以:
如果此時weight為0(n=530),說明第54輪到0就停止了,那麼:
2) 十位
對於10位來說,其0-9週期的出現次數與個位的統計方式是相同的,見圖:
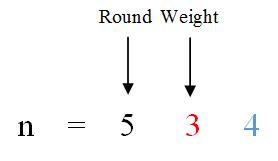
不同點在於:從1到n,每增加10,十位的weight才會增加1,所以,一輪0-9週期內,1會出現10次。即rount*10。
再來看weight的值。當此時weight為3,大於1,說明第6輪出現了10次1,則:
如果此時weight的值等於0(n=504),說明第6輪到0就停止了,所以:
如果此時weight的值等於1(n=514),那麼第6輪中1出現了多少次呢?很明顯,這與個位數的值有關,個位數為k,第6輪中1就出現了k+1次(0-k)。我們記個位數為former,則:
3) 更高位
更高位的計算方式其實與十位是一致的,不再闡述。
4) 總結
將n的各個位分為兩類:個位與其它位。
對個位來說:
- 若個位大於0,1出現的次數為
round*1+1 - 若個位等於0,1出現的次數為
round*1
對其它位來說,記每一位的權值為base,位值為weight,該位之前的數是former,舉例如圖:
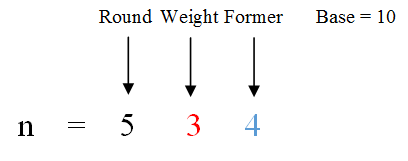
則:
- 若weight為0,則1出現次數為
round*base - 若weight為1,則1出現次數為
round*base+former+1
- 若weight大於1,則1出現次數為
rount*base+base
當某一位的數字小於k時,那麼該位出現i的次數為:更高位數字x當前位數
當某一位的數字等於k時,那麼該位出現i的次數為:更高位數字x當前位數+低位數字+1
當某一位的數字大於k時,那麼該位出現i的次數為:(更高位數字+1)x當前位數
程式碼:
package Solution19;
// 求出1~13的整數中1出現的次數,並算出100~1300的整數中1出現的次數?
// 為此他特別數了一下1~13中包含1的數字有1、10、11、12、13因此共出現6次,但是對於後面問題他就沒轍了。
// ACMer希望你們幫幫他,並把問題更加普遍化,可以很快的求出任意非負整數區間中1出現的次數。
public class Solution {
public int NumberOf1Between1AndN_Solution(int n) {
if (n < 1)
return 0;
int count = 0;
int base = 1;
int round = n;
while (round > 0) {
int weight = round % 10; //round的最後一位數,從個位數開始
round /= 10;
count += round * base;
if (weight == 1)
count += (n % base) + 1;
else if (weight > 1)
count += base;
base *= 10;
}
return count;
}
}
6. 時間複雜度分析
由分析思路或者程式碼都可以看出,while迴圈的次數就是n的位數,logn(以10為底),而迴圈體內執行的操作都是有限次的,所以時間複雜度為O(logn)。
變型:計算數字k在0到n中的出現的次數,k可能是0~9的一個值
分析:此情形需要特殊考慮k=0的情況,其餘情況與上述k=1情況類似。
//計算數字k在0到n中的出現的次數,k可能是0~9的一個值
public int digitCounts(int k, int n) {
// write your code here
if(n<1 || k<0) return 0;
if(k==0 && n<10) return 1; //考慮特殊情況
int count=0;
int base=1;
int round=n;
while(round>0){
int weight=round %10; //round的最後一位,從個位開始
round/=10;
count+=round*base; //更高位數字*當前位數
if(weight==k){
count+=(n%base)+1;
}else if(weight<k){
count+=0;
}else{
if(!(k==0 && round==0)){ //排除沒有更高位時,尋找的數為0的情況 這種情況如n=19,k=0的情況,0為最高位時不應再加10
count+=base;
}
}
base*=10;
}
return count;
}