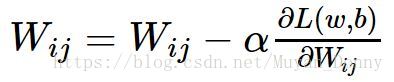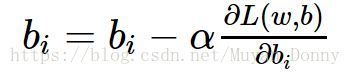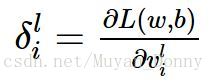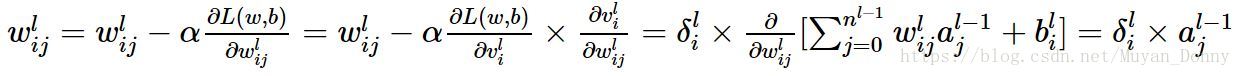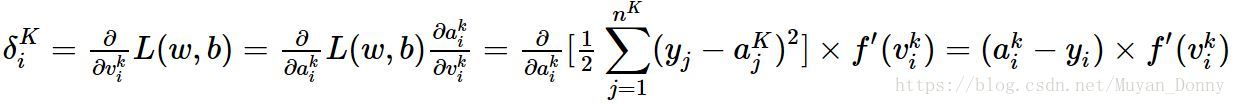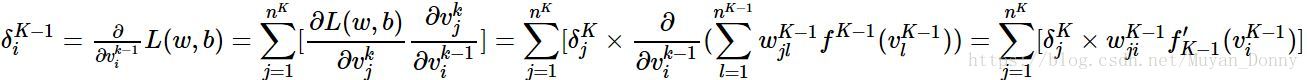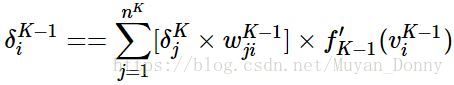梯度下降方法是常用的引數優化方法，經常被用在神經網路中的引數更新過程中。

神經網路中，將樣本中的輸入X和輸出Y當做已知值（對於一個樣本[X,Y]，其中X和Y分別是標準的輸入值和輸出值，X輸入到模型中計算得到Y，但是模型中的引數值我們並不知道，所以我們的做法是隨機初始化模型的引數，不斷更新迭代這些引數，使得模型的輸出與Y接近），將連線權和偏置值當做自變數，誤差L（損失函式的值）作為因變數。梯度下降的目的是找到全部連線權和偏置值在取何值的情況下誤差最小。

經常有人把梯度下降的過程比作從山頂走到谷底，一次走多遠比作“學習率”。那麼，它 的數學表現形式是什麼呢？

這就是梯度下降演算法的迭代公式，當梯度下降為零時，w、b收斂，訓練結束

反向傳播思想可以用來方便的求出損失函式對每個引數的導數，其基本原理是求導數時的鏈式法則。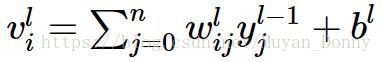 

其中，Vil表示第l層第i個節點的值，yj(l-1)表示第（l-1）層第幾個節點輸出的值（也即啟用值aj(l-1)） 

定義殘差為：

則迭代公式根據鏈式法則可改寫為 ：

 這兩個公式寫的都有點錯誤，前面兩個等號內容是連線權和偏置值迭代的演算；後兩個等號內容是損失函式對連線權和偏置值的偏導。

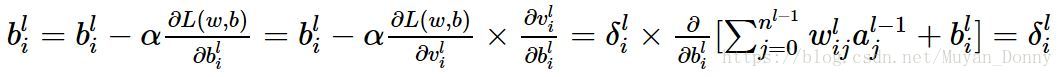
 是表示第（l-1）層的第 j 個節點的啟用值，即，f（）為該節點的啟用函式。

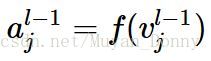
利用殘差可以以統一的形式表示各層節點的連線權和偏置值的迭代公式。那麼，各層節點處的殘差是怎麼計算的呢？

這就是反向傳播演算法設計的內容，反向傳播過程的細節如下：

（1）隨機初始化網路中各層的引數：連線權和偏置值，通常將它們隨機初始化為均值為0、方差為0.01的隨機數

（2）對輸入資料進行前向計算，從輸入層到輸出層，依次計算每一層的每個節點的值v以及啟用值a

（3）計算最後一層節點的“殘差”。對於神經網路的最後一層輸出層，因為可以直接算出網路產生的啟用值與實際值之間的差距，所以很容易計算損失函式對最後一層的偏導數。假設第K層為輸出層，則：

即輸出層的第 i 個節點的殘差為：（該點的啟用值-該點的真實值）*該點啟用函式對該點值得導數 

（4）對於第K-1層的殘差，可以根第K層的殘差計算出來：

簡而言之： 

（多打了一個“=”） 

也就是說，前一層某個神經元的殘差 是由後一層中每個神經元貢獻的，其貢獻的份額是由二者之間的連線權決定的，並且作用上前一層啟用函式的導數。

（5）逐層計算每個節點的殘差值，根據（4）中的結果，用 K-2 代替 K-1，用 K-1 代替 K 則得到 K-2 層的殘差。以此類推可以得到前面各層的連線權和偏置值得殘差。

（6）根據連線權和偏置值的梯度下降法迭代公式即可得到其新的迭代值。

（7）當我們輸入一個訓練樣本室，就可以根據（2）-（6），對W和b進行更新。