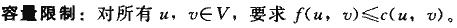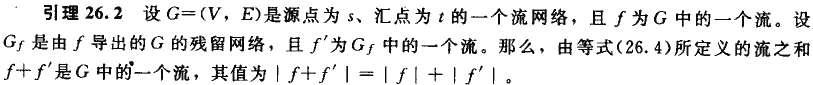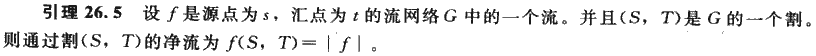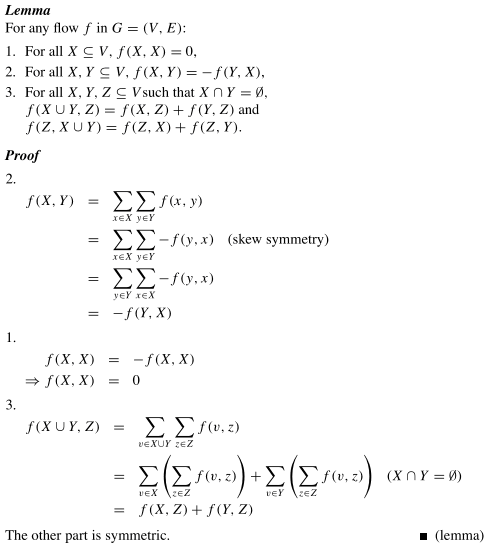第26章 最大流(正在修改)
一、綜述
1.定義
定義1:流網路
定義2:殘留容量
定義3:增廣路徑
已知一個網路流G=(V,E)和流f,增廣路徑p為殘留網路G|f中從s到t的一條簡單路徑
能夠沿一條增廣路徑p的每條邊傳輸的網路流的最大量為p的殘留容量,由下式定義:
c|f(p) = min{c|f(u,v) : (u,v)在p上}
定義4:割、淨流、容量、最小割
淨流和容量的區別:
穿過(S,T)的淨流由雙向的正網路流組成;在加上從S到T的正網路流的同時,減去從T到S的正網路流。
割(S,T)的容量僅由從S到T的連計算而得。從T到S的邊在計算c(S,T)時是不算在內的。
2.性質
3.定理
定理1:
定理2:
定理3:
定理4:
定理5:
定理6:
對一個網路流G中任意流f來說,其值的上介面為G的任意割的容量
定理7:
二、程式碼
版本一:最大流,圖用矩陣實現,求增廣路徑用BELLMAN-FORD實現
1.Mat_Flow.h
#include <iostream> using namespace std; #define NMAX 210 class Mat_Flow { public: int n;//點的個數。其中0是源點,1是匯點 int map[NMAX][NMAX];//網路費用 int net[NMAX][NMAX];//剩餘網路 int path[NMAX];//增廣路徑,path[v]=u說明(u,v)在增廣路徑上 int ecost[NMAX];//源點到各點的最短路徑 Mat_Flow(int num):n(num) { memset(map, 0, sizeof(map)); } void AddSingleEdge(int start, int end, int value = 1) { map[start][end] = value; } void MakeGraph(int m); bool bellman_ford(); int max_flow(); }; void Mat_Flow::MakeGraph(int m) { int start, end, value; while(m--) { cin>>start>>end>>value; AddSingleEdge(start, end, value); } } bool Mat_Flow::bellman_ford() { int i, j; memset(path, -1, sizeof(path)); fill(ecost, ecost+NMAX, INT_MAX); ecost[0] = 0; bool flag = true; while(flag) { flag = false; for(i = 0; i <= n; i++) { if(ecost[i] == INT_MAX) continue; for(j = 0; j <= n; j++) { if(net[i][j] > 0 && ecost[i] + 1 < ecost[j]) { flag = true; ecost[j] = ecost[i] + 1; path[j] = i; } } } } return ecost[n] != INT_MAX; } int Mat_Flow::max_flow() { int i, j; //初始時,剩餘網路即為整個網路 for(i = 0; i <= n; i++) { for(j = 0; j <= n; j++) net[i][j] = map[i][j]; } int maxflow = 0; //while there exists a path p from s to t int the residual network G1 //從剩餘網路中找到一條增廣路徑,增廣路徑存在在path中 while(bellman_ford()) { //do c|f(p) <- min {c|f(u,v):(u,v) is in p} //計算增廣路徑上的淨流 int v = n, cfp = INT_MAX, u; while(v != 0) { //path儲存的是增廣路徑,path[v]=u說明(u,v)在增廣路徑上 u = path[v]; cfp = min(cfp, net[u][v]); v = u; } //更新最大流的大小 maxflow += cfp; //更新剩餘網路 //for each edge(u,v) in p v = n; while(v != 0) { u = path[v]; //f[u,v] <- f[u,v] + cfp net[u][v] -= cfp; net[v][u] += cfp; //f[v,u] <- -f[u,v] v = u; } } return maxflow; }
2.main.cpp
#include "Mat_flow.h"
/*
5 10
0 1 16
0 2 13
1 3 12
1 2 10
2 1 4
3 2 9
2 4 14
3 5 20
4 3 7
4 5 4
*/
int main()
{
int n, m;
while(cin>>n>>m)
{
Mat_Flow *G = new Mat_Flow(n);
G->MakeGraph(m);
cout<<G->max_flow()<<endl;
delete G;
}
return 0;
}
3.測試資料
《演算法導論》P405圖26-5
4.執行結果
版本2:矩陣+HLPP(高度標號預流推進演算法)
1."Mat_HLPP_Flow.h"
2.main.cpp
#include "Mat_HLPP_Flow.h"
/*
5 10
0 1 16
0 2 13
1 3 12
1 2 10
2 1 4
3 2 9
2 4 14
3 5 20
4 3 7
4 5 4
*/
int main()
{
int n, m;
while(cin>>n>>m)
{
Mat_HLPP_Flow *G = new Mat_HLPP_Flow(n);
G->MakeGraph(m);
cout<<G->high_label_preflow_push()<<endl;
delete G;
}
return 0;
}
3.測試資料與測試結果
同上
三、練習
26.1 網路流
26.1-1
定義1:如果(u,v)不屬於E,c(u,v)=0
性質1:f(u,v) <= c(u,v)
====> 如果(u,v)不屬於E,f(u,v) = 0。
反向邊同理
26.1-2
性質2,反對稱性
26.1-3
待解決
26.1-4
26.1-5
(1)f(X,Y)=-f(V-X,Y)
X:t Y:v3,v4
(2)f(X,Y)!=-f(V-X,Y)
X:v3,v4 Y:v1,v2
26.1-6
必定滿足“反對稱性”和“流守恆性”,可能違反“容量限制”
26.1-7
由26.1-6知,af1+(1-a)f2滿足“反對稱性”和“流守恆性”。
因為f1和f2滿足“容量限制”,因此af1+(1-a)f2滿足“容量限制”
所以af1+(1-a)f2也是流
26.1-8
在網路中每一節點流入流出的量應該相等

例如上圖,可以寫出以下等式:
x1 – x3 –x4 = 0
x2 + x3 – x5 = 0
26.1-9
將地圖轉換為一個有向圖:
(1)每個角落作為一個頂點
(2)若一個角落到另一個角落有路,則構成有向圖的邊。
(3)每條路構成正向和反向兩條邊,容量都是1
計算該有向圖的最大流,若最大流大於或等於2,則“可以”26.2Ford-Fulkerson方法
26.2-1
淨流:19
容量:31
26.2-2
26.2-3
最大流的最小割是23第二條增廣路徑的第二段和第三條增廣路徑的第2段抵消
第一條增廣路徑的第三段和第四條增廣路徑的第2段抵消
26.2-4
根據反對稱性和殘留網路定義
c|f(u,v) + c|f(v,u)
= c(u,v) - f(u,v) + c(v,u) - f(v,u)
= c(u,v) + c(v,u)
26.2-5
根據流守恆性
26.2-6
22.2-7
似乎是很顯然的事情
26.2-8
不知道題目是什麼意思,討厭證明題
26.2-9
構造這樣一個帶權有向圖G2,
G2的頂點和G是一樣的。若G中存在一條(u,v)的邊,則在G2中加一條u->v的邊,和一條v->u的邊,權值都是1.
在G2的基礎上構造|V|個網路流,依次令|V|個頂點分別做為匯點,再選一個不是匯點的點做為源點。依次求這|V|個網路流的最大流。
這|V|個網路流的最小值即為G的邊連通度
26.3最大二分匹配
26.3-1
26.3-2
又見證明題
26.3-3
2*min(|L|, |R|)+1
26.4 壓入與重標記法
26.5重標記與前移演算法
四、思考題
26-1逃脫問題
(1)構造網路流G,令m個點為G的源點,令邊界點中不是源點的點為G的匯點。
(2)若兩個頂點相鄰,則構造兩條有向邊,邊權為1