分類問題是機器學習的研究重點，而後者在實踐中常常碰到非均衡資料集這個難題。非均衡資料集（imbalanced data）又稱為非平衡資料集，指的是針對分類問題，資料集中各個類別所佔比例並不平均。

比如在網路廣告行業，需要對使用者是否點選網頁上的廣告進行建模。為了處理方便，我們記“點選廣告”為類別1，“不點選廣告”為類別0。因此這是一個二元分類問題。在訓練模型的歷史資料裡有1000個數據點（1000行），其中類別1的資料點只有10個，剩下的990個數據全部為類別0。這就是一個非均衡資料集，類別之間的比例為99:1。與二元分類問題類似，多元分類問題同樣會面對非均衡資料集這個難題。不過在這個問題上，多元分類的處理的方案與二元的相似，因此為了表述簡潔利於理解，下面的討論將針對二元分類問題。

非均衡資料集在現實中是十分常見的。它給模型搭建帶來了困難，如果不小心處理，會導致得到的模型結果毫無意義。在討論這個話題之前，讓我們稍稍離題一下，來看看所謂的準確度悖論（accuracy paradox）。

注意：本篇文章的完整程式碼在*這裡下載***

一、準確度悖論

對於二元分類問題，模型的預測結果按準確與否可以分為如下4類，見表1。

其中，TP和TN這兩個部分都表示模型的預測結果是正確的，這兩者之和的比例越高，說明模型的效果越好。由此可以定義評估模型效果的指標——準確度（accurary，ACC）。

$ACC = \frac{TP + TN}{TP + FP + FN + TN} \tag{1}$

準確度這個指標看似很合理，但面對非均衡資料集時，這個指標會嚴重失真，甚至變得毫無意義。來看下面這個例子：資料集裡有1000個數據點，其中990個為類別0，而剩下的10個為類別1，如圖1所示。

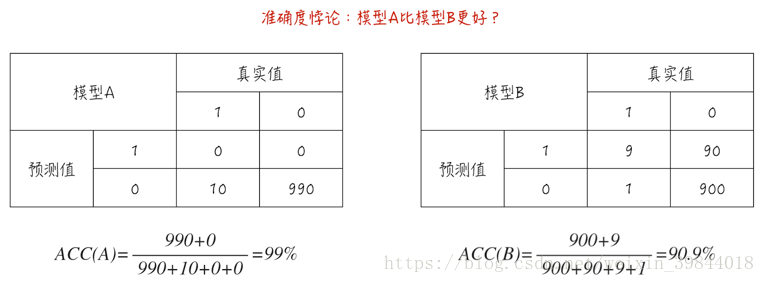
模型A對所有資料的預測都是類別0，因此這個模型其實並沒有提供什麼預測功能。但它的準確度卻高達99%。模型B的預測效果其實很不錯：對於類別1，10個數據裡有9個預測正確；而對於類別0，990個數據裡有900個預測正確，但它的準確度只有90.9%遠低於模型A。
這就是所謂的準確度悖論：面對非均衡資料集時，準確度這個評估指標會使模型嚴重偏向佔比更多的類別，導致模型的預測功能失效。這也是之前文章（

二、一個例子

非均衡資料集除了會引起準確度悖論外，它對搭建模型有什麼影響呢？下面通過一個簡單的例子來說明這個問題。我們按公式（2）產生模型資料，其中變數$y$為因變數；$x_1, x_2$為自變數；$\varepsilon$為隨機擾動項，它服從邏輯分佈。

$y = \begin{cases}1, x_1 - x_2 + \varepsilon > 0 \\0, else \end{cases}\tag{2}$

由此可見，產生的模型資料完美地符合邏輯迴歸模型的假設。因此使用邏輯迴歸對資料建模，得到結果按理說應該非常好。但事實上，當資料集是均衡時，也就是說類別1所佔比例大約為0.5時，模型效果是還不錯。但當類別1所佔比例接近0時，也就是資料集是非均衡時，模型的效果就很差了。雖然資料集裡類別1的個數不變，但模型的預測結果幾乎都是類別0，如圖2a所示。正如上面討論的那樣，ACC這個指標在非均衡資料集裡會失真，而AUC則可以保持穩定，能正確衡量模型的好壞，如圖2b所示。

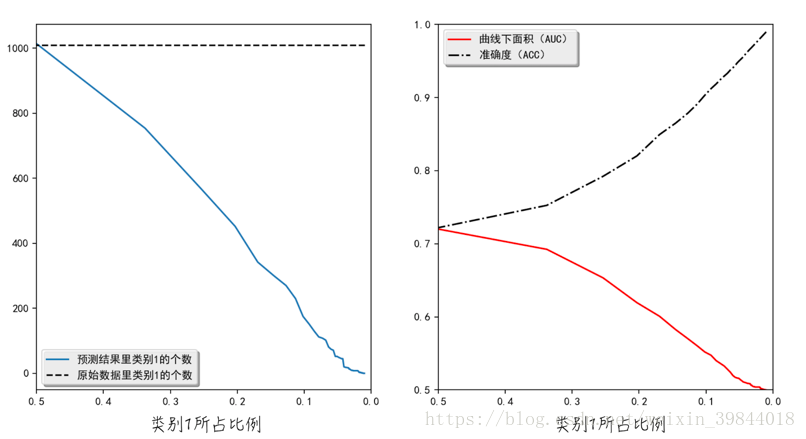
上面的例子從直觀上展示了非均衡資料集對搭建模型的影響。那麼造成這種結果的原因是什麼呢？從數學角度來講，邏輯迴歸引數的估算公式如下：（懲罰項並不影響這裡的討論，因此我們在此省略掉懲罰項。）

$h(X_i) = \frac{1}{1 + e^{-X_i\beta}}\\ \hat{\beta} = argmin_{\beta}\sum_i -y_i\ln h(X_i) - (1 - y_i)\ln [1 - h(X_i)] \tag{3}$

在這個公式裡，每個資料點的權重都是一樣的，都為1。也就是說，模型對於類別1所承受的損失為：$-y_i\ln h(X_i)$。這個值幾乎等於模型對於類別0所承受的損失：$-(1 - y_i)\ln [1 - h(X_i)]$。如果某一類別的資料特別多，不妨假定為類別0，那麼在類別1某點的附件，極有可能存在大量的類別0。在這種情況下，根據公式（3），模型會選擇“犧牲”類別1，從而導致預測結果幾乎都為類別0。

上面的結論並不只針對邏輯迴歸這個分類模型，對於其他分類模型，也同樣成立。

三、解決方法

針對非均衡資料集，最常見也是最方便的解決方案是修改損失函式裡不同類別的權重。以邏輯迴歸為例，將它的損失函式改寫為公式（4）。

$\hat{\beta} = argmin_{\beta}\sum_i -w_1y_i\ln h(X_i) - w_0(1 - y_i)\ln [1 - h(X_i)] \tag{4}$

當類別1所佔比例很少時，則增加$w_1$，也就是增加模型對於類別1所承受的損失，反之亦然。在大多數情況下，類別權重的選擇原則是，類別權重等於類別所佔比例的倒數，如程式清單1中**第7、8行程式碼所示**。經過權重調整後，訓練模型的資料集相當於回到了均衡狀態。權重調整的程式碼非常簡單，如第10行程式碼所示，通過“class_weight”引數調整各個類別的權重。事實上，“class_weight”也可以被賦值為“balanced”，即“class_weight= ‘balanced’”，這時模型會自動調整各個類別的權重。

程式清單1 非平衡資料集

 1	|  from sklearn.linear_model import LogisticRegression
 2	|  
 3	|  def balanceData(X, Y):
 4	|      """
 5	|      通過調整各個類別的比重，解決非均衡資料集的問題
 6	|      """
 7	|      positiveWeight = len(Y[Y>0]) / float(len(Y))
 8	|      classWeight = {1: 1. / positiveWeight, 0: 1. / (1 - positiveWeight)}
 9	|      # 為了消除懲罰項的干擾，將懲罰係數設為很大
10	|      model = LogisticRegression(class_weight=classWeight, C=1e4)
11	|      model.fit(X, Y.ravel())
12	|      pred = model.predict(X)
13	|      return pred

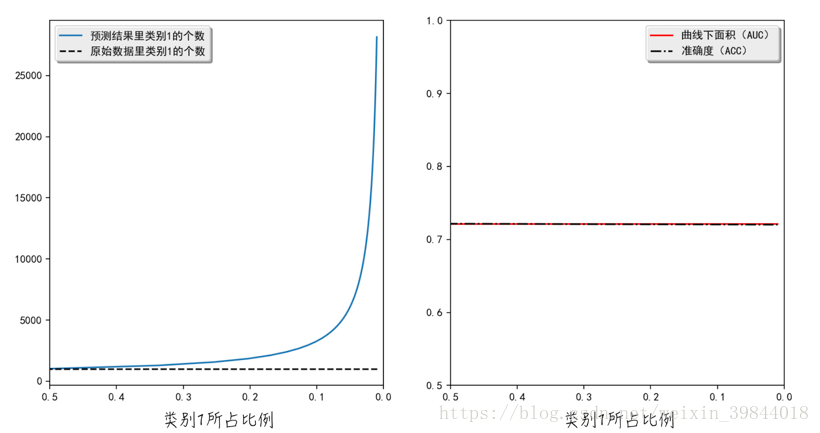
經過權重調整後，模型的結果如圖3所示。在處理非均衡資料集時，調整權重後的模型會錯誤地將很多類別0的資料預測為類別1。這與我們之前在上一節裡的分析是一致的：類別1的權重增加後，模型會因“刻意地珍惜”類別1，而選擇“犧牲”類別0。儘管如此，調整之後的整體效果明顯優於調整之前的（調整之後的AUC更大）。值得注意的是，ACC和AUC這兩個評估指標幾乎相等，所以圖形上它們兩者重疊在了一起。

對於非均衡資料集，還有一些其他的解決方法，比如通過重新抽樣（sampling），把多的類別變少或把少的類別變多。具體的細節在此就不做展開討論了。

四、廣告時間

李國傑院士和韓家煒教授在讀過此書後，親自為其作序，歡迎大家購買。

另外，與之相關的免費視訊課程請關注這個連結