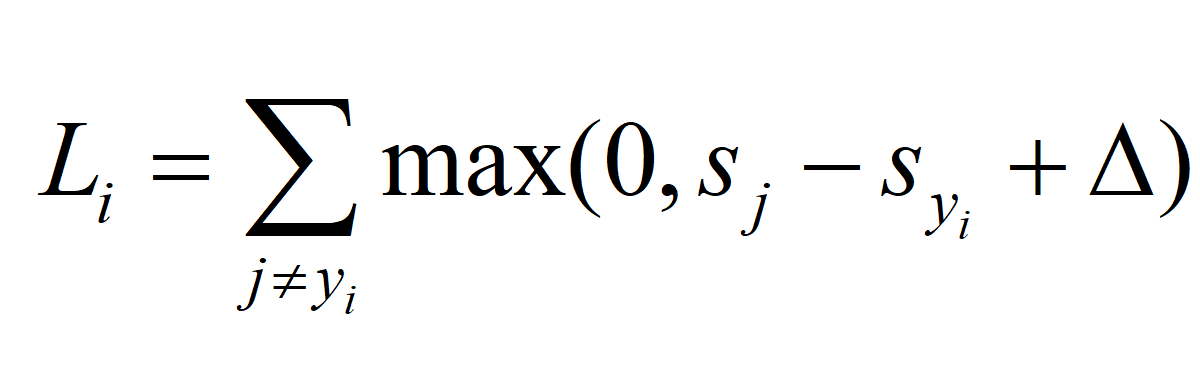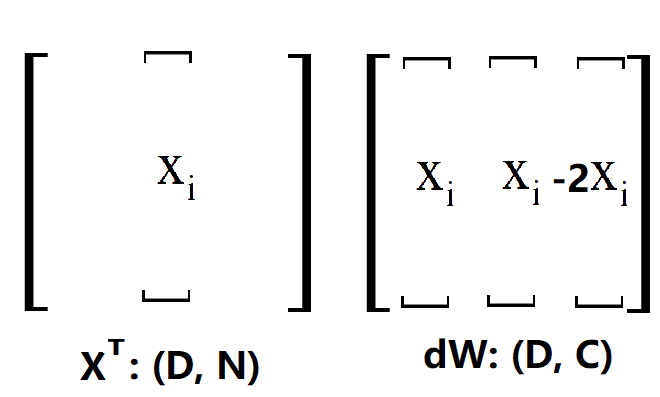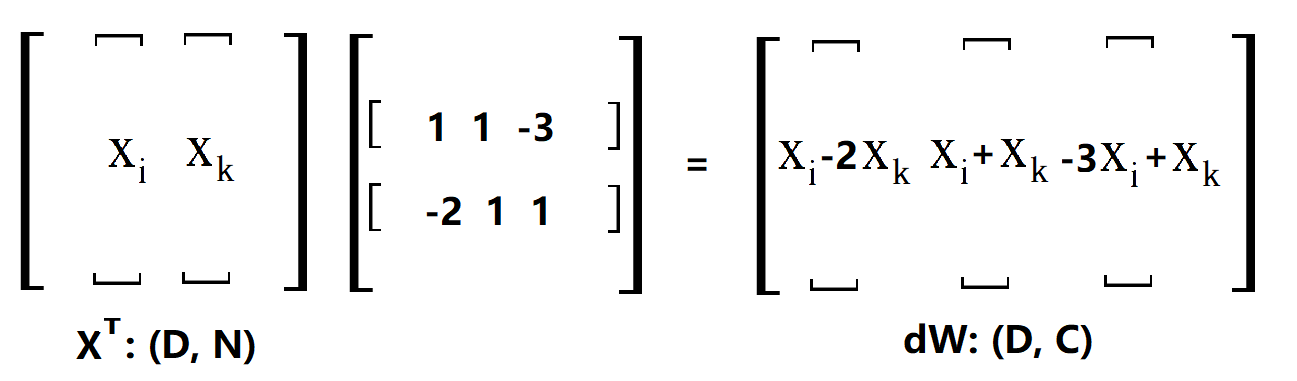個人覺得svm和softmax的梯度部分是這份作業的難點，參考了一些程式碼覺得還是難以理解，網上似乎也沒有相關的解釋，所以想把自己的想法貼出來，提供一個參考。

        首先貼上參考的程式碼：

    def svm_loss_vectorized(W, X, y, reg):  
      """ 
      Structured SVM loss function, vectorized implementation. 
     
      Inputs and outputs are the same as svm_loss_naive. 
      """  
      loss = 0.0  
      num_train= X.shape[0]  
      dW = np.zeros(W.shape) # initialize the gradient as zero  
      scores = np.dot(X,W)  
      correct_class_scores = scores[np.arange(num_train),y]  
      correct_class_scores = np.reshape(correct_class_scores,(num_train,-1))  
      margin = scores-correct_class_scores+1.0  
      margin[np.arange(num_train),y]=0.0  
      margin[margin<=0]=0.0                   # ** #  
      loss += np.sum(margin)/num_train  
      loss += 0.5*reg*np.sum(W*W)  
      
      margin[margin>0]=1.0                    # ** #  
      row_sum = np.sum(margin,axis=1)          # ** #  
      margin[np.arange(num_train),y] = -row_sum  # ** #  
      dW = 1.0/num_train*np.dot(X.T,margin) + reg*W  # ** #  
      
     return loss, dW  
 

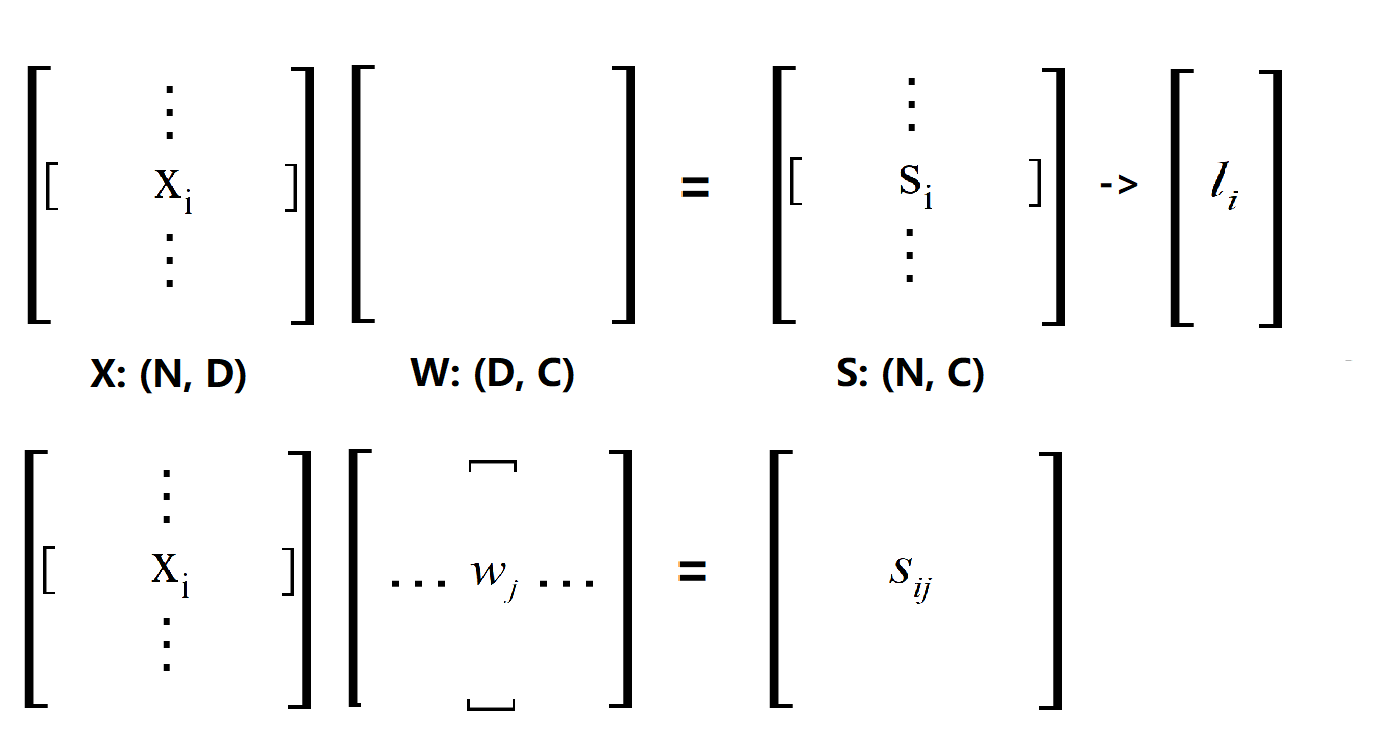
        難以理解的地方就是打星號的幾行，也就是求梯度的程式碼。我們首先看看這個Loss是怎麼來的，應該不用多說看下圖（這裡點乘的順序和程式碼中的一致）:

        X·W得到的S矩陣，對應程式碼中的scores，然後根據給出的公式（y是正確類的序號向量）：

        得到 L 矩陣（或者說 L 向量，要注意公式給出的只是計算一條樣本的loss），然後求和得到最終的Loss，前面的不用多說。接下來是難點，如何求Loss對W的梯度，首先我們將公式寫成原來的樣子:

        求Loss的過程是先對 i 求和，再對 j 求和的過程，那我們直接用 L(ij)來分析，L(ij)的來源是什麼？首先 max（）函式後面一部分要大於0，不然對 L(ij) 沒有貢獻，然後 j != y(i) ，因為 j == y(i) 壓根就不算進公式裡面，所以 L(ij) 的來源是 j != y(i) 的情況下，max（）函式後面要大於0 的部分

，那麼要給W更新，自然也是這一部分，怎麼更新的呢？哦我們給dw(j) 加上 x(i), 同時要給dw(y(i)) 加上 -x(i) 就可以了。要注意的是，在上面這個公式裡面，i 不是求和的變數，所以 x(i) 我們可以看成是等著被加的東西，我們看下面一副圖 (delta == 1, 與程式碼一致)：

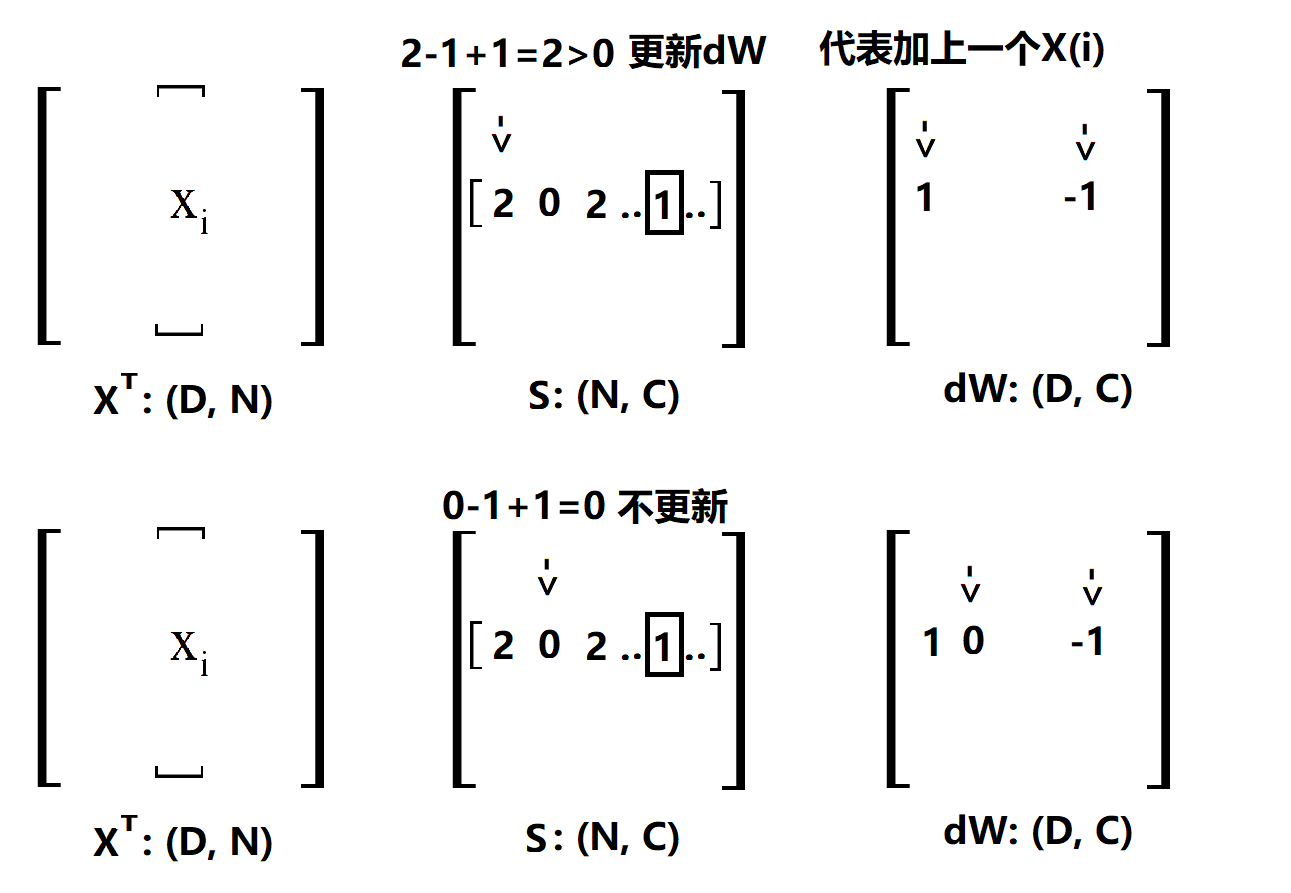
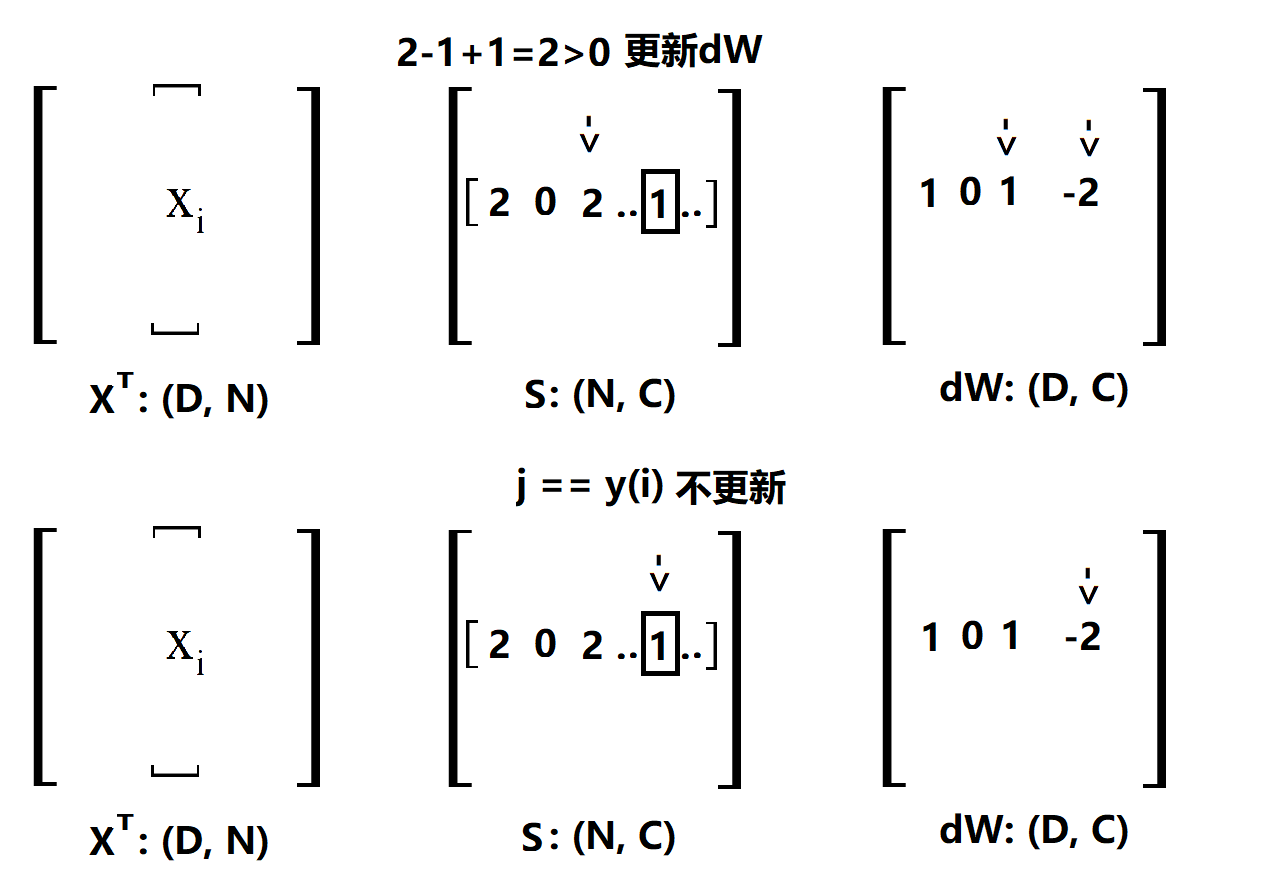
        說明一下，一行一行的來看，首先確定一個 i，然後掃描 S(i)，這裡的 S 就是 X·W，沒處理過之前的scores，用方框框住的表示正確類。第一個是2，計算max（）的結果為2，所以更新dW，那麼我要在dW的第一個位置加 x(i) 在 y(i) 的位置加 -x(i), 為了方便後面解釋，這裡寫1就表示加一個 x(i) ，-1就表示加一個 -x(i)。第二個位置是0，max（）結果是0，不更新，後面類似。經過上面的4步，最後得到的dW是這樣的（將就著看一看）：

        OK，其實這裡已經很清楚了，剛剛做出來的是一個用於更新的向量 [ 1 0 1 .. -2 ..]，只要用 XT 點乘這個更新的向量就可以得到dW了，這很容易理解，因為對這個更新向量裡面的值，比如說第一個1，相當於用這個1數乘x(i)。當然了，上面只是對第 i 條樣本做的更新，因為我們是看 L(ij) 的，所以還要把剩下的樣本都做一次，程式碼中的margin就是所有的更新向量放在一起而已，比如說這樣（向量不止3個，不然不會出現-3）：

       迴歸到程式碼，我們再看看是怎麼處理這個更新向量：

      margin[np.arange(num_train),y]=0.0  
      margin[margin>0]=1.0  
      row_sum = np.sum(margin,axis=1)  
      margin[np.arange(num_train),y] = -row_sum  

        程式碼當中一開始的margin是在S矩陣的基礎上算好了 s(j) - s(y(i))+1 的矩陣，這樣就可以直接判斷是否需要更新，第一步把所有y的位置置0，第二步把>0的位置置1，這樣，只有s(j) - s(y(i))+1>0 且 j != y(i) 的位置為1，第三步計算一行中有多少個1，在第4步為y的位置置為這個數的負數， 就是因為在掃描 S[i] 的過程中，每有一個 w(j) 要更新就要同時更新 w(y(i)) 的緣故，這和之前的分析一致。

        這是個人的一些理解，如果有出錯的，希望大家能夠指出。