單層前饋神經網路（SLFN）以其良好的學習能力在許多領域得到了廣泛的應用，然而傳統的學習演算法，如BP等固有的一些缺點，成為制約其發展的主要瓶頸，前饋神經網路大多采用梯度下降法，該方法存在以下幾個方面的缺點和不足：

1、訓練速度慢。由於梯度下降法需要多次迭代，從而達到修正權值和閾值的目的，因此訓練過程耗時較長；

2、容易陷入區域性極小值，無法到達全域性最小；

3、學習率yita的選擇敏感，學習率對神經網路的效能影響較大，必須選擇合適的才能達到較為理想的效果，太小則演算法的收斂速度很慢，訓練過程耗時較長，太大，則訓練過程可能不穩定。

本文將介紹一種新的SLFN的演算法，極限學習機，該演算法將隨機產生輸入層和隱含層間的連線權值和隱含層神經元的閾值，且在訓練過程中無需調整，只需要設定隱含層的神經元的個數，便可以獲得唯一最優解，與傳統的訓練方法相比，該方法具有學習速率快、泛化效能好等優點。

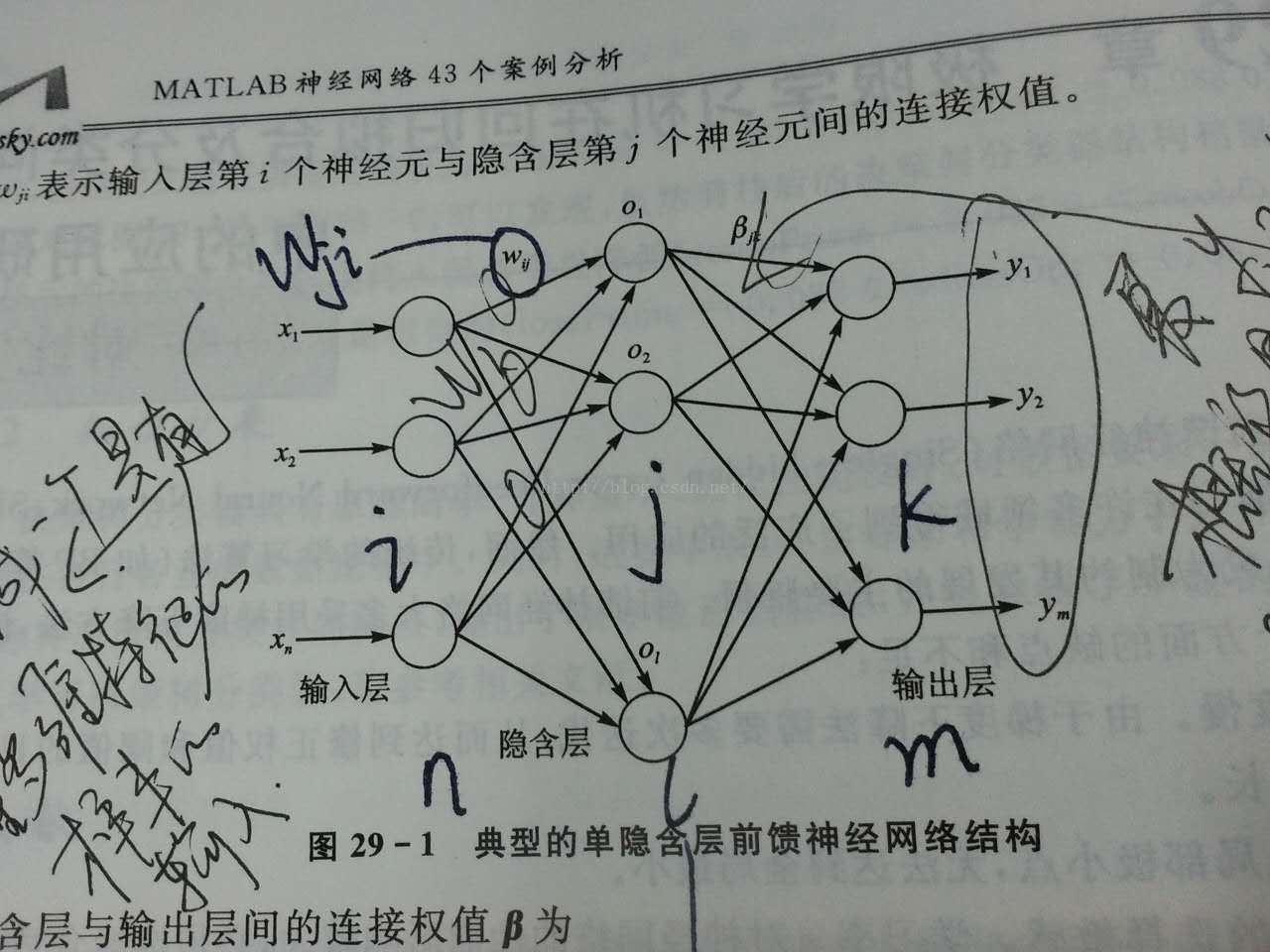
先上一張圖（畫圖太麻煩，直接拍的照）

典型的單隱層前饋神經網路如上圖所示，輸入層與隱含層，隱含層與輸出層之間是全連線的。輸入層的神經元的個數是根據樣本的而特徵數的多少來確定的，輸出層的神經元的個數是根據樣本的種類數來確定的

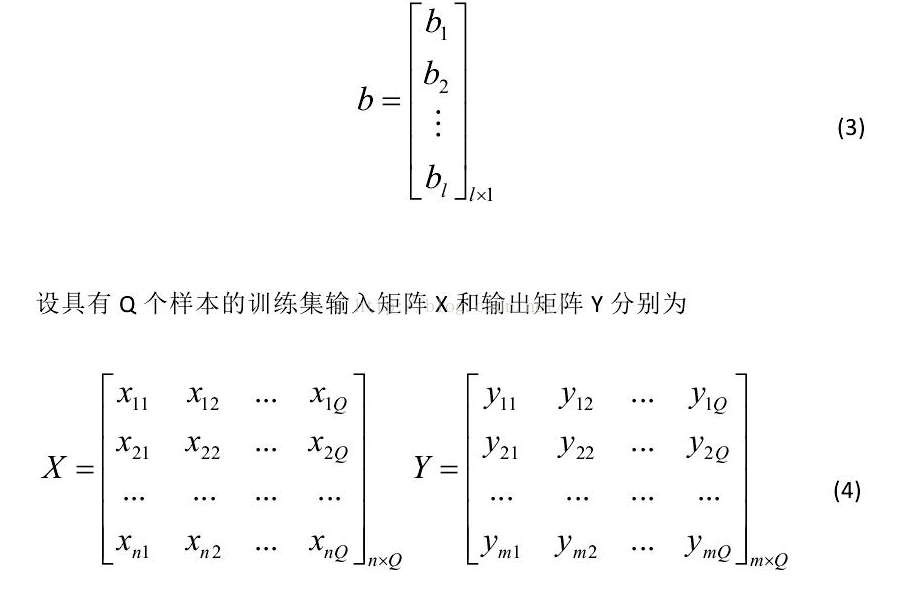
設隱含層神經元的閾值 b為：

當隱層神經元的個數和樣本數相同時（10）式有唯一的解，也就是說零誤差的逼近訓練樣本。通常的學習演算法中，W和b需要不斷進行調整，但研究結果告訴我們，他們事實上是不需要進行不斷調整的，甚至可以隨意指定。調整他們不僅費時，而且並沒有太多的好處。（此處有疑慮，可能是斷章取義，這個結論有可能是基於某個前提下的）。

總結一下：ELM與BP都是基於前饋神經網路的架構之下的，他們的不同之處在於學習的方法不同，BP是通過梯度下降法，利用反向傳播的方式進行的學習，需要不斷地進行迭代來更新權重和閾值，而ELM則是通過增加隱層節點的個數來達到學習的目的，隱層節點的個數一般是根據樣本的個數來確定的，巧妙地將隱含層的個數與樣本的個數進行了聯絡。其實在許多前向神經網路中，預設的最大的隱層節點的個數就是樣本數，（如RBF）。它不需要進行迭代，所以速度就比BP要快很多。ELM的精華之處就在於那兩條他所依賴的定理，這些定理決定了他的學習方式。輸入層和隱含層之間的權重w和隱含層節點的閾值b是通過隨機初始化得到的，而且不需要進行調整。一般隱層節點的個數與樣本的個數相同（在樣本數比較少的情況下）。

ELM的matlab程式碼可以直接在網上下到，而且原理也很簡單，ELMtrain的過程就是為了計算隱含層與輸出層之間的權重，是根據標籤矩陣T利用公式11得到的，ELMpredict則是利用隱含層與輸出層之間的權重來計算輸出T，當然也會將ELMtrain中的隨機初始化的輸入節點和隱層節點之間的權值和隱層節點的閾值照搬過來，不會再進行隨機初始化（否則隱層與輸出層之間的權值不就白計算了嘛，因為他們就是根據ELMtrain中隨機初始化的那些值計算得到的呀）所以整個極限學習機還是很簡單的。

極限學習機是一種學習方式，深度學習也可以和極限學習機相結合，例如ELM-AE

極限學習機與徑向基神經網路的思想如出一轍，通過增加隱層神經元的個數可以實現將線性不可分的樣本對映到高層的線性可分的空間，然後再通過隱層與輸出層之間進行線性劃分，完成分類功能，不過徑向基的啟用函式是用的徑向基函式，相當於svm中的核函式（徑向基核函式）

在看完了徑向基神經網路之後，發現極限學習機必是受了RBF的思想影響。因為RBF也是隱層結點個數儘量多，而且嚴格徑向基網路就是要求隱層結點個數與輸入樣本個數相等，並且隱層神經元與輸出層神經元之間也是線性加權得到的最終的輸出，隱層與輸出層之間的權值，RBF是通過解線性方程得到的，極限學習機也是通過隱層輸出的廣義逆矩陣進行線性方程的求解得到的。

定理一是對應的RBF中的 正則化的RN（通用逼近器），即隱層結點個數=輸入樣本個數，定理二是對應的RBF中的 廣義網路GN（模式分類器），隱層節點<輸入樣本數，個人感覺極限學習機是融合了RBF和BP兩種演算法的學習思想，輸入層與隱層之間是BP，隱層與輸出層之間是RBF，當然隱層節點的個數也是慣用了RBF的兩種形式，即RN和GN