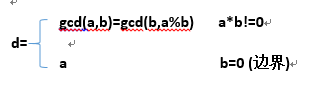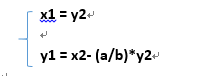一：歐幾里得演算法
1，歐幾里德演算法又稱為輾轉相除法，主要用於計算兩個整數a,b的最大公約數。
2，原理：

//遞迴寫法
int gcd(int a,int b)
{
    if(b==0)
        return a;
    return gcd(b,a%b);
}
//非遞迴的
int gcd(int a,int b)
{
    while(b)
    {
        int t=a;
        a=b;
        b=t%b;
    }
    return a;
}

二：歐幾里得擴充套件原理：
1，對於不完全為 0 的非負整數 a，b，d=gcd（a，b）表示 a，b 的最大公約數，必然存在整數對 x，y ，使得d=ax+by成立。歐幾里得擴充套件原理就是求x，y的演算法。
2，推倒：
(1) 若 d=0 很顯然 x=1 y=0 ；使得 ax+by=d=a。
(2) 若 d！=0
由上面的歐幾里得演算法可以得到 gcd(a,b)=gcd(b,a%b); 於是我們假設存在兩對實數(x1，y1) 與 (x2，y2) ，使得 ：
x1*a+y1*b=gcd(a,b) ， x2*b+y2*(a%b)=gcd(b,a%b) 成立。
所以有 x1*a+y1*b = x2*b+y2*(a%b) ，而 a%b=(a-（a/b)*b）代入原式中得到 ：
x1*a+y1*b = x2*b+y2*((a-（a/b)*b）)=y2*a +（x2- (a/b)*y2）*b 所以：
可以得到遞推公式：

int ex_gcd(int a,int b,int &x,int &y)
{
    if(b==0)
    {
        x=1; y=0;
        return a;
    }
    int d=ex_gcd(b,a%b,y,x);
    y=y-(a/b)*x;
    return d;
}