自己的總結：

1、輸入層到隱藏層之間不是通過權值和閾值進行連線的，而是通過輸入樣本與隱藏層點之間的距離（與中心點的距離）連線的。

2、得到距離之後，將距離代入徑向基函式，得到一個數值。數值再與後邊的權值相乘再求總和，就得到了相應輸入的輸出。

3、在訓練網路之前，需要確定中心點的個數，和中心點的位置。以及求出隱藏層各徑向基函式的方差（寬窄程度）。和隱藏層和輸出層之間的權值。

4、中心點個數、中心點位置、方差、權值都可以通過下文所述的方法求出來。

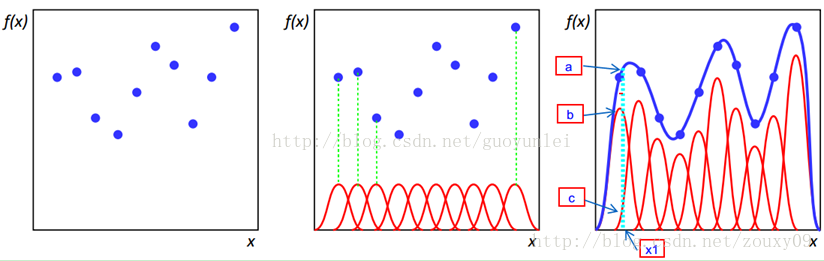
5、徑向基函式也是一種基，可以通過對其線性組合，來對非線性函式進行擬合。

6、RBF神經網路只需要瞭解其中的原理。然後給了訓練資料，求出上述幾個引數，再輸入測試資料，就可以預測輸出了。

如第三個圖，徑向基函式的

RBF網路能夠逼近任意的非線性函式，可以處理系統內的難以解析的規律性，具有良好的泛化能力，並有很快的學習收斂速度，已成功應用於非線性函式逼近、時間序列分析、資料分類、模式識別、資訊處理、影象處理、系統建模、控制和故障診斷等。

簡單說明一下為什麼RBF網路學習收斂得比較快。當網路的一個或多個可調引數（權值或閾值）對任何一個輸出都有影響時，這樣的網路稱為全域性逼近網路。由於對於每次輸入，網路上的每一個權值都要調整，從而導致全域性逼近網路的學習速度很慢。BP網路就是一個典型的例子。

如果對於輸入空間的某個區域性區域只有少數幾個連線權值影響輸出，則該網路稱為區域性逼近網路。常見的區域性逼近網路有RBF網路、小腦模型（CMAC）網路、B樣條網路等。

徑向基函式解決插值問題

完全內插法要求插值函式經過每個樣本點，即。樣本點總共有P個。

RBF的方法是要選擇P個基函式，每個基函式對應一個訓練資料，各基函式形式為，由於距離是徑向同性的，因此稱為徑向基函式。||X-X^p||表示差向量的模，或者叫2範數。

基於為徑向基函式的插值函式為：

輸入X是個m維的向量，樣本容量為P，P>m。可以看到輸入資料點X^p是徑向基函式φ_p的中心。

隱藏層的作用是把向量從低維m對映到高維P，低維線性不可分的情況到高維就線性可分了。

將插值條件代入：

寫成向量的形式為，顯然Φ是個規模這P對稱矩陣，且與X的維度無關，當Φ可逆時，有。

對於一大類函式，當輸入的X各不相同時，Φ就是可逆的。下面的幾個函式就屬於這“一大類”函式：

1）Gauss（高斯）函式

2）Reflected Sigmoidal（反常S型）函式

3）Inverse multiquadrics（擬多二次）函式

σ稱為徑向基函式的擴充套件常數，它反應了函式影象的寬度，σ越小，寬度越窄，函式越具有選擇性。

完全內插存在一些問題：

1）插值曲面必須經過所有樣本點，當樣本中包含噪聲時，神經網路將擬合出一個錯誤的曲面，從而使泛化能力下降。

由於輸入樣本中包含噪聲，所以我們可以設計隱藏層大小為K，K<P，從樣本中選取K個（假設不包含噪聲）作為Φ函式的中心。

2）基函式個數等於訓練樣本數目，當訓練樣本數遠遠大於物理過程中固有的自由度時，問題就稱為超定的，插值矩陣求逆時可能導致不穩定。

擬合函式F的重建問題滿足以下3個條件時，稱問題為適定的：

1. 解的存在性
2. 解的唯一性
3. 解的連續性

不適定問題大量存在，為解決這個問題，就引入了正則化理論。

正則化理論

正則化的基本思想是通過加入一個含有解的先驗知識的約束來控制對映函式的光滑性，這樣相似的輸入就對應著相似的輸出。

尋找逼近函式F(x)通過最小化下面的目標函式來實現：

加式的第一項好理解，這是均方誤差，尋找最優的逼近函式，自然要使均方誤差最小。第二項是用來控制逼近函式光滑程度的，稱為正則化項，λ是正則化引數，D是一個線性微分運算元，代表了對F(x)的先驗知識。曲率過大（光滑度過低）的F(x)通常具有較大的||DF||值，因此將受到較大的懲罰。

直接給出(1)式的解：

權向量********************************(2)

G(X,X^p)稱為Green函式，G稱為Green矩陣。Green函式與運算元D的形式有關，當D具有旋轉不變性和平移不變性時，。這類Green函式的一個重要例子是多元Gauss函式：

。

正則化RBF網路

輸入樣本有P個時，隱藏層神經元數目為P，且第p個神經元採用的變換函式為G(X,X^p)，它們相同的擴充套件常數σ。輸出層神經元直接把淨輸入作為輸出。輸入層到隱藏層的權值全設為1,隱藏層到輸出層的權值是需要訓練得到的：逐一輸入所有的樣本，計算隱藏層上所有的Green函式，根據(2)式計算權值。

廣義RBF網路

Cover定理指出：將複雜的模式分類問題非線性地對映到高維空間將比投影到低維空間更可能線性可分。

廣義RBF網路：從輸入層到隱藏層相當於是把低維空間的資料對映到高維空間，輸入層細胞個數為樣本的維度，所以隱藏層細胞個數一定要比輸入層細胞個數多。從隱藏層到輸出層是對高維空間的資料進行線性分類的過程，可以採用單層感知器常用的那些學習規則，參見神經網路基礎和感知器。

注意廣義RBF網路只要求隱藏層神經元個數大於輸入層神經元個數，並沒有要求等於輸入樣本個數，實際上它比樣本數目要少得多。因為在標準RBF網路中，當樣本數目很大時，就需要很多基函式，權值矩陣就會很大，計算複雜且容易產生病態問題。另外廣RBF網與傳統RBF網相比，還有以下不同：

1. 徑向基函式的中心不再限制在輸入資料點上，而由訓練演算法確定。
2. 各徑向基函式的擴充套件常數不再統一，而由訓練演算法確定。
3. 輸出函式的線性變換中包含閾值引數，用於補償基函式在樣本集上的平均值與目標值之間的差別。

因此廣義RBF網路的設計包括：

結構設計--隱藏層含有幾個節點合適

引數設計--各基函式的資料中心及擴充套件常數、輸出節點的權值。

下面給出計算資料中心的兩種方法：

1. 資料中心從樣本中選取。樣本密集的地方多采集一些。各基函式採用統一的偏擴充套件常數：
   
   
   d_max是所選資料中心之間的最大距離，M是資料中心的個數。擴充套件常數這麼計算是為了避免徑向基函式太尖或太平。
2. 自組織選擇法，比如對樣本進行聚類、梯度訓練法、資源分配網路等。各聚類中心確定以後，根據各中心之間的距離確定對應徑向基函式的擴充套件常數。

   
   
   λ是重疊係數。

接下來求權值W時就不能再用了，因為對於廣義RBF網路，其行數大於列數，此時可以求Φ偽逆。

 資料中心的監督學習演算法

最一般的情況，RBF函式中心、擴充套件常數、輸出權值都應該採用監督學習演算法進行訓練，經歷一個誤差修正學習的過程，與BP網路的學習原理一樣。同樣採用梯度下降法，定義目標函式為

e_i為輸入第i個樣本時的誤差訊號。

上式的輸出函式中忽略了閾值。

為使目標函式最小化，各引數的修正量應與其負梯度成正比，即

具體計算式為

上述目標函式是所有訓練樣本引起的誤差總和，匯出的引數修正公式是一種批處理式調整，即所有樣本輸入一輪後調整一次。目標函式也可以為瞬時值形式，即當前輸入引起的誤差

此時引數的修正值為：

下面我們就分別用本文最後提到的聚類的方法和資料中心的監督學習方法做一道練習題。

考慮Hermit多項式的逼近問題

訓練樣本這樣產生：樣本數P=100，x_i且服從[-4,4]上的均勻分佈，樣本輸出為F(x_i)+e_i，e_i為新增的噪聲，服從均值為0，標準差為0.1的正態分佈。

（1）用聚類方法求資料中心和擴充套件常數，輸出權值和閾值用偽逆法求解。隱藏節點數M=10，隱藏節點重疊係數λ=1，初始聚類中心取前10個訓練樣本。