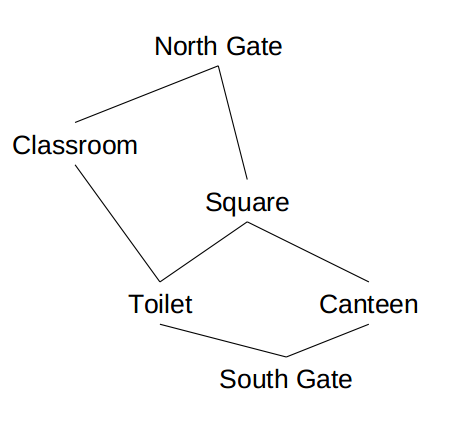
我們用字串代表圖的頂點(vertax)，來模擬學校中Classroom, Square, Toilet, Canteen, South Gate, North Gate幾個地點，然後計算任意兩點之間的最短路徑。

如，我想從North Gate去Canteen, 程式的輸出結果應為：

    BFS: From [North Gate] to [Canteen]:
    North Gate
    Square
    Canteen

首先定義一個演算法介面Algorithm:

public interface Algorithm {
    /**
     * 執行演算法
     */
 

    void perform(Graph g, String sourceVertex);

    /**
     * 得到路徑
     */
    Map<String, String> getPath();
}

然後，定義圖:

/**
 * (無向)圖
 */
public class Graph {
    // 圖的起點
    private String firstVertax;

    // 鄰接表
    private Map<String, List<String>> adj = new HashMap<>();

    // 遍歷演算法
 

    private Algorithm algorithm;

    public Graph(Algorithm algorithm) {
        this.algorithm = algorithm;
    }

    /**
     * 執行演算法
     */
    public void done() {
        algorithm.perform(this, firstVertax);
    }

    /**
     * 得到從起點到{@code vertex}點的最短路徑
     * @param vertex
     * @return
     */
 

    public Stack<String> findPathTo(String vertex) {
        Stack<String> stack = new Stack<>();
        stack.add(vertex);

        Map<String, String> path = algorithm.getPath();
        for (String location = path.get(vertex) ; false == location.equals(firstVertax) ; location = path.get(location)) {
            stack.push(location);
        }
        stack.push(firstVertax);

        return stack;
    }

    /**
     * 新增一條邊
     */
    public void addEdge(String fromVertex, String toVertex) {
        if (firstVertax == null) {
            firstVertax = fromVertex;
        }

        adj.get(fromVertex).add(toVertex);
        adj.get(toVertex).add(fromVertex);
    }

    /**
     * 新增一個頂點
     */
    public void addVertex(String vertex) {
        adj.put(vertex, new ArrayList<>());
    }

    public Map<String, List<String>> getAdj() {
        return adj;
    }
}

這裡我們使用策略設計模式，將演算法與Graph類分離，通過在構造Graph物件時傳入一個Algorithm介面的實現來為Graph選擇遍歷演算法。

public Graph(Algorithm algorithm) {
        this.algorithm = algorithm;
    }

無向圖的儲存結構為鄰接表，這裡用一個Map表示鄰接表，map的key是學校地點(String)，value是一個與該地點相連通的地點表(List<String>)。

// 鄰接表
    private Map<String, List<String>> adj = new HashMap<>();

然後，編寫Algorithm介面的BFS實現：

/**
 * 封裝BFS演算法
 */
public class BroadFristSearchAlgorithm implements Algorithm {
    // 儲存已經訪問過的地點
    private List<String> visitedVertex;
    // 儲存最短路徑
    private Map<String, String> path;


    @Override
    public void perform(Graph g, String sourceVertex) {
        if (null == visitedVertex) {
            visitedVertex = new ArrayList<>();
        }
        if (null == path) {
            path = new HashMap<>();
        }

        BFS(g, sourceVertex);
    }

    @Override
    public Map<String, String> getPath() {
        return path;
    }

    private void BFS(Graph g, String sourceVertex) {
        Queue<String> queue = new LinkedList<>();
        // 標記起點
        visitedVertex.add(sourceVertex);
        // 起點入列
        queue.add(sourceVertex);

        while (false == queue.isEmpty()) {
            String ver = queue.poll();

            List<String> toBeVisitedVertex = g.getAdj().get(ver);
            for (String v : toBeVisitedVertex) {
                if (false == visitedVertex.contains(v)) {
                    visitedVertex.add(v);
                    path.put(v, ver);
                    queue.add(v);
                }
            }
        }
    }
}

其中，path是Map型別，意為從 value 到 key 的一條路徑。
BFS演算法描述：
1. 將起點標記為已訪問並放入佇列。
2. 從佇列中取出一個頂點，得到與該頂點相通的所有頂點。
3. 遍歷這些頂點，先判斷頂點是否已被訪問過，如果否，標記該點為已訪問，記錄當前路徑，並將當前頂點入列。
4. 重複2、3，直到佇列為空。

測試用例：

String[] vertex = {"North Gate", "South Gate", "Classroom", "Square", "Toilet", "Canteen"};
    Edge[] edges = {
            new Edge("North Gate", "Classroom"),
            new Edge("North Gate", "Square"),
            new Edge("Classroom", "Toilet"),
            new Edge("Square", "Toilet"),
            new Edge("Square", "Canteen"),
            new Edge("Toilet", "South Gate"),
            new Edge("Toilet", "South Gate"),
    };

@Test
    public void testBFS() {
        Graph g = new Graph(new BroadFristSearchAlgorithm());
        addVertex(g);
        addEdge(g);
        g.done();

        Stack<String> result = g.findPathTo("Canteen");
        System.out.println("BFS: From [North Gate] to [Canteen]:");
        while (!result.isEmpty()) {
            System.out.println(result.pop());
        }
    }