說明

在IEEE標準中，浮點數在記憶體中的表示是將特定長度的連續位元組的所有二進位制位按特定長度劃分為符號域，指數域和尾數域三個連續域。

float

float型別在記憶體中佔用的位數為: 1+8+23=32bits

double

1+11+52=64bits

第一位s代表符號為，1代表負數，0代表正數。

第二個域是指數域，對於單精度float型別，指數域有８位，可以表示　0-255個指數值。指數值規定了小數點的位置，小數點的移動代表了所表示數值的大小。但是，指數可以為正數，也可以為負數。為了處理負指數的情況，實際的指數值按要求需要加上一個偏差（Bias）值作為儲存在指數域中的值，單精度數的偏差 值為 -127，而雙精度double型別的偏差值為 -1023。比如，單精度指數域中的64 則表示實際的指數值 -63。 偏差的引入使得對於單精度數，實際可以表達的指數值的範圍就變成-127 到 128 之間（包含兩端）。我們不久還將看到，實際的指數值-127（儲存為 全 0）以及 +128（儲存為全1）保留用作特殊值的處理

第三個域為尾數域，其中單精度數為 23 位長，雙精度數為 52 位長。比如一個單精度尾數域中的值為: 00001001000101010101000, 第二個域中的指數值則規定了小數點在尾數串中的位置，預設情況下小數點位於尾數串首位之前。　　

比如指數值為　-1,則該float數即為：.000001001000101010101000,如果為+1,則該float 數值為:0.0001001000101010101000。我們知道引入浮點數的目的在於用盡可能少的位數表示既高精度又大範圍的實數，其中的範圍大小是由指數域位長確定的，而尾數域的長度則確定了所能表示實數的精度，所以double比float數的精度更高，範圍更大，相應的也就佔用更多的記憶體。　剛才我們介紹的對尾數域中的值的解釋並不能實現這個精度最大化的目標，因為在尾數串第一個”1”之前還有４個”0”,這4個”0”實際上是多餘的，因為我們把小數點向前移動時，前端的＂０＂是自動新增的，所以可以把這４個“0”刪除，然後尾數域末端多出４個位來表示更高精度的數值。也就是說尾數的第一位一定是＂１＂，那麼既然第一位一定是＂１＂，那麼我們也就沒有必要把它儲存在尾數域中，而是直接預設尾數為1.xxxx…xxx的形式。尾數的首位從小數點後開始。那麼上面的例子所表示的尾數就是：
1.00001001000101010101000。　用23位表示了24位的資訊 (小數點不佔位置).

表示

一個規格化的32位浮點數ｘ的真值為：

x=(−1)^s × (1.M) × 2^E−127

一個規格化的64位浮點數ｘ的真值為：

x=(−1)^s × (1.M) × 2^E−1023

下面舉一個32位單精度浮點數-3.75表示的例子幫助理解：

(1) 首先轉化為2進製表示

−3.75=−(2+1+1/2+1/4)=−1.111×2^1

(2) 整理符號位並進行規格化表示

−1.111×21=(−1)(1)×(1+0.1110 0000 0000 0000 0000 000)×2^1

(3) 進行階碼的移碼處理

(−1)^(1)×(1+0.1110 0000 0000 0000 0000 000)×2^1

=(−1)^(1)×(1+0.1110 0000 0000 0000 0000 000)×2^128−127

於是，符號位S=1，尾數M為1110 0000 0000 0000 0000 000階碼E為128_10=1000 0000_2,則最終的32位單精度浮點數為1 1110 0000 0000 0000 0000 000 1000 0000

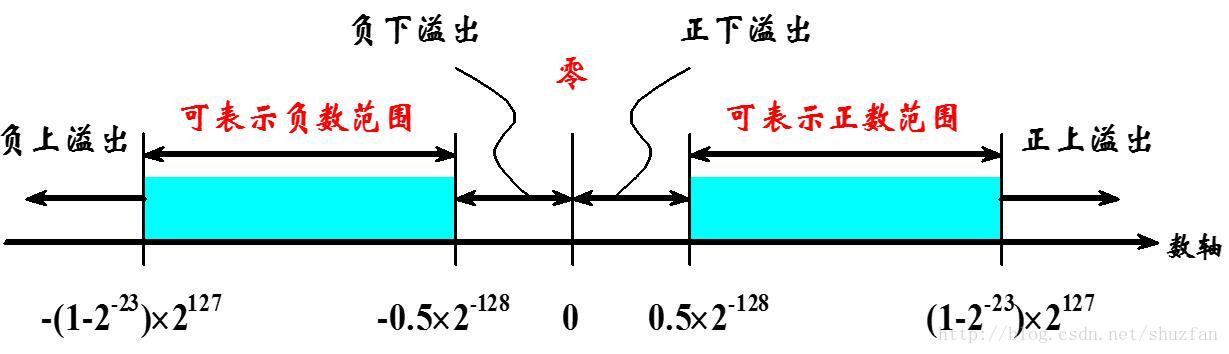
浮點數表示範圍與精度

通過上面的規格化表示，我們可以很容易確定浮點數的表示範圍：

一般提到浮點數的精度（有效位數）的時候，總是會出現 float的有效位為6~7位, double的有效位為15~16位 。

既然有表示範圍，那肯定也有不能表示的數值：

下面以float為例，解釋一下有效位數是怎樣來的。

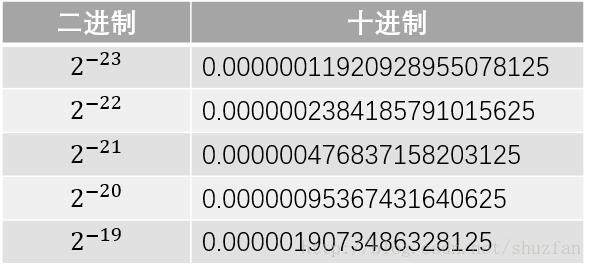
有效位數只和規格化浮點數的尾數部分有關，而尾數部分的位數是23位，因此我們首先列出下表

由上面的表格可以看出：

2−23 和 2−22 之間是存在間隔的，即0.0000001和0.0000002之間的小數我們是沒有辦法描述的，因此23位尾數最多隻能描述到小數點後第7位；此外，我們通過四捨五入可以很容易發現0.0000003=0.0000004=2−23+2−22, 這表明第7位有效數字只是部分準確。而第6位及之前的都是可以準確描述的，因此我們說float的有效位為6~7位。

例子

參考資料：