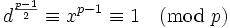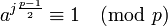二次剩餘--尤拉準則
阿新 • • 發佈:2019-01-27
在數論中,二次剩餘的尤拉判別法(又稱尤拉準則)是用來判定給定的整數是否是一個質數的二次剩餘。
 是
是 的一個原根,因此
的一個原根,因此 模
模 的指數是
的指數是 ,於是
,於是 整除
整除 。這說明
。這說明 是一個偶數。令
是一個偶數。令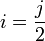 ,就有
,就有 。
。 是模
是模
目錄
敘述
若 是奇質數且
是奇質數且 不能整除
不能整除 ,則:
,則:
 是模
是模 的二次剩餘當且僅當:
的二次剩餘當且僅當:
 是模
是模 的非二次剩餘當且僅當:
的非二次剩餘當且僅當:
以勒讓德符號表示,即為:
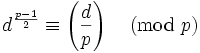
舉例
例子一:對於給定數,尋找其為二次剩餘的模數
令a = 17。對於怎樣的質數p,17是模p的二次剩餘呢?
根據判別法裡給出的準則,我們可以從小的質數開始檢驗。
首先測試p = 3。我們有:17(3 − 1)/2 = 171 ≡ 2 (mod 3) ≡ -1 (mod 3),因此17不是模3的二次剩餘。
再來測試p = 13。我們有:17(13 − 1)/2 = 176 ≡ 1 (mod 13),因此17是模13的二次剩餘。實際上我們有:17 ≡ 4 (mod 13),而22
運用同餘性質和勒讓德符號可以加快檢驗速度。繼續算下去,可以得到:
- 對於質數p =
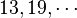 ,(17/p) = +1(也就是說17是模這些質數的二次剩餘)。
,(17/p) = +1(也就是說17是模這些質數的二次剩餘)。 - 對於質數p =
 ,(17/p) = -1(也就是說17是模這些質數的二次非剩餘)。
,(17/p) = -1(也就是說17是模這些質數的二次非剩餘)。
例子二:對指定的質數p,尋找其二次剩餘
哪些數是模17的二次剩餘?
我們可以手工計算:
- 12 = 1
- 22 = 4
- 32 = 9
- 42 = 16
- 52 = 25 ≡ 8 (mod 17)
- 62 = 36 ≡ 2 (mod 17)
- 72 = 49 ≡ 15 (mod 17)
- 82 = 64 ≡ 13 (mod 17)
於是得到:所有模17的二次剩餘的集合是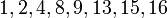 。要注意的是我們只需要算到8,因為9=17-8,9的平方與8的平方模17是同餘的:92
。要注意的是我們只需要算到8,因為9=17-8,9的平方與8的平方模17是同餘的:92
但是對於驗證一個數是不是模17的二次剩餘,就不必將所有模17的二次剩餘全部算出。比如說要檢驗數字3是否是模17的二次剩餘,只需要計算3(17 − 1)/2 = 38 ≡ 812 ≡ ( − 4)2 ≡ − 1 (mod 17),然後由尤拉準則判定3不是模17的二次剩餘。
尤拉準則與高斯引理以及二次互反律有關,並且在定義尤拉-雅可比偽素數(見偽素數)時會用到。
證明
首先,由於 是一個奇素數,由費馬小定理,
是一個奇素數,由費馬小定理, 。但是
。但是 是一個偶數,所以有
是一個偶數,所以有
 是一個素數,所以
是一個素數,所以 和
和  中必有一個是
中必有一個是 的倍數。因此
的倍數。因此 模
模 的餘數必然是1或-1。
的餘數必然是1或-1。
- 證明若
 是模
是模 的二次剩餘,則
的二次剩餘,則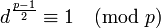
- 證明若
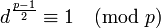 ,則
,則 是模
是模 的二次剩餘
的二次剩餘
 是一個奇素數,所以關於
是一個奇素數,所以關於 的原根存在。設
的原根存在。設 是
是 的一個原根,則存在
的一個原根,則存在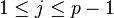 使得
使得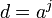 。於是
。於是
 是
是 的一個原根,因此
的一個原根,因此 模
模 的指數是
的指數是 ,於是
,於是 整除
整除 。這說明
。這說明 是一個偶數。令
是一個偶數。令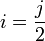 ,就有
,就有 。
。 是模
是模

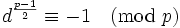
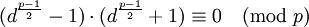
 ,
,