SVM支援向量機-SKlearn實現與繪圖(8)
瞭解了SVM的基本形式與演算法實現,接下來用SKlearn實現支援向量機分類器.
1.函式定義與引數含義
先看一下SVM函式的完全形式和各引數含義:
SVC(C=1.0, kernel=’rbf’, degree=3, gamma=’auto’, coef0=0.0, shrinking=True, probability=False, tol=0.001, cache_size=200, class_weight=None, verbose=False, max_iter=-1, decision_function_shape=’ovr’, random_state=None)
這裡只介紹一部分,其餘引數可以參考SKlearn.SVM
C:懲罰係數,default = 1.0,同軟間隔中的鬆弛因子
kernel:核函式選擇,default = "rbf",可選 ‘linear’(線性核函式), ‘poly’(多項式核函式), ‘rbf’(高斯核函式), ‘sigmoid’(siigmoid核函式), ‘precomputed’
degree:多項式核函式poly的項數,只有使用poly核函式才會呼叫,其他核函式會忽略
class_weight:{dict,'balanced'},樣本權重,預設均等權重
decision_function_shape:拆分策略,預設ovr,ovo一對一1策略被捨棄
random_state:隨機數生成種子
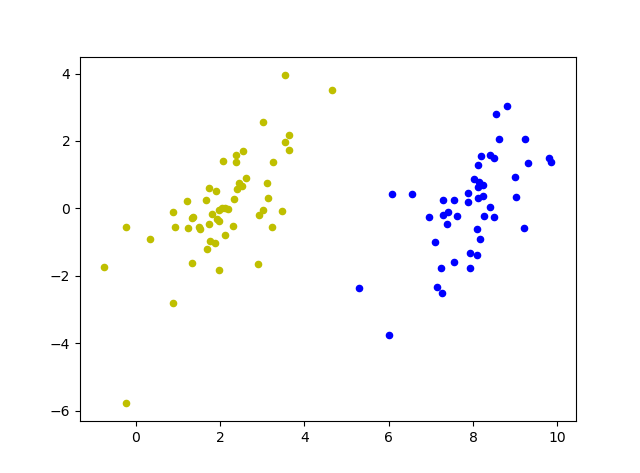
2.線性可分情況的SVM
1)匯入相關庫與資料讀取函式
#Sklearn SVM支援向量機 from sklearn.svm import SVC import matplotlib.pyplot as plt import numpy as np from sklearn.model_selection import train_test_split def loadDataSet(fileName): dataMat = []; labelMat = [] fr = open(fileName) for line in fr.readlines(): lineArr = line.strip().split('\t') dataMat.append([float(lineArr[0]), float(lineArr[1])]) labelMat.append(float(lineArr[2])) return dataMat,labelMat
2)通過SKlearn返回的引數繪製超平面
def plot_point(dataArr,labelArr,Support_vector_index,W,b):
for i in range(np.shape(dataArr)[0]):
if labelArr[i] == 1:
plt.scatter(dataArr[i][0],dataArr[i][1],c='b',s=20)
else:
plt.scatter(dataArr[i][0],dataArr[i][1],c='y',s=20)
for j in Support_vector_index:
plt.scatter(dataArr[j][0],dataArr[j][1], s=100, c = '', alpha=0.5, linewidth=1.5, edgecolor='red')
x = np.arange(0,10,0.01)
y = (W[0][0]*x+b)/(-1*W[0][1])
plt.scatter(x,y,s=5,marker = 'h')
plt.show()3)主函式
if __name__ == "__main__":
#讀取資料,針對二維線性可分資料
dataArr,labelArr = loadDataSet('testSet.txt')
#定義SVM分類器
clf = SVC(C=1.0, cache_size=200, class_weight=None, coef0=0.0,
decision_function_shape='ovr', degree=3, gamma='auto', kernel='linear',
max_iter=-1, probability=False, random_state=None, shrinking=True,
tol=0.001, verbose=False)
#fit訓練資料
clf.fit(dataArr, labelArr)
#獲取模型返回值
n_Support_vector = clf.n_support_#支援向量個數
Support_vector_index = clf.support_#支援向量索引
W = clf.coef_#方向向量W
b = clf.intercept_#截距項b
#繪製分類超平面
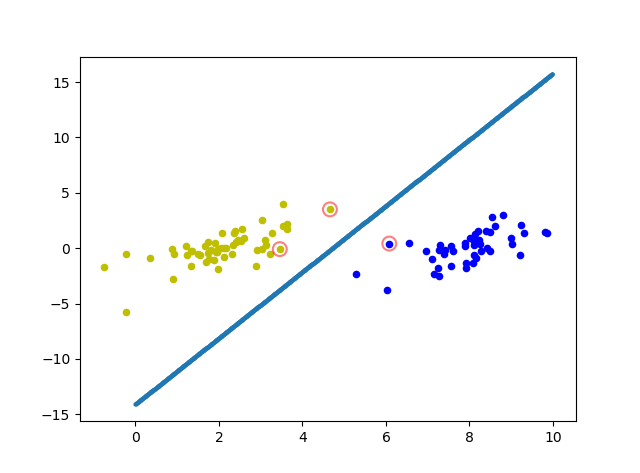
plot_point(dataArr,labelArr,Support_vector_index,W,b)clf.n_support_返回支援向量個數1,會返回一個1x2的列表,分別表示決策函式兩邊各有幾個支撐向量
clf.suspport_返回支援向量的索引,通過對應索引,即可在圖中標記支援向量
clf.coef_返回方向向量W,即超平面引數
clf.intercept_返回超平面截距項b
tips:這裡幾種用法只有kernel=“linear”才可以上使用,而其他幾種核函式無法呼叫,所以我們這裡只能在二維繪製超平面.
4)執行結果
3.線性不可分情況的SVM
1)匯入相關庫與讀取資料
#Sklearn SVM支援向量機
from sklearn.svm import SVC
import matplotlib.pyplot as plt
import numpy as np
from sklearn.model_selection import train_test_split
def loadDataSet(fileName):
dataMat = []; labelMat = []
fr = open(fileName)
for line in fr.readlines():
lineArr = line.strip().split('\t')
dataMat.append([float(lineArr[0]), float(lineArr[1])])
labelMat.append(float(lineArr[2]))
return dataMat,labelMat2)標記支援向量
def plot_point(dataArr,labelArr,Support_vector_index):
for i in range(np.shape(dataArr)[0]):
if labelArr[i] == 1:
plt.scatter(dataArr[i][0],dataArr[i][1],c='b',s=20)
else:
plt.scatter(dataArr[i][0],dataArr[i][1],c='y',s=20)
for j in Support_vector_index:
plt.scatter(dataArr[j][0],dataArr[j][1], s=100, c = '', alpha=0.5, linewidth=1.5, edgecolor='red')
plt.show()由於沒有使用線性核函式,所以沒有呼叫w,b,只標記支援向量
3)主函式
if __name__ == "__main__":
#讀取資料,針對二維線性不可分資料
dataArr,labelArr = loadDataSet('testSetRBF.txt')
for i in range(np.shape(dataArr)[0]):
if labelArr[i] == 1:
plt.scatter(dataArr[i][0],dataArr[i][1],c='b',s=20)
else:
plt.scatter(dataArr[i][0],dataArr[i][1],c='y',s=20)
plt.show()
#交叉驗證劃分資料集,train:test = 0.8 : 0.2
X_train, X_test, y_train, y_test = train_test_split(dataArr,labelArr, test_size=.2,random_state = 0)
#初始化模型引數
clf = SVC(cache_size=200, class_weight=None, coef0=0.0,C=1.0,
decision_function_shape='ovr', degree=3, gamma='auto', kernel='rbf',
max_iter=-1, probability=False, random_state=None, shrinking=True,
tol=0.001, verbose=False)
clf.fit(X_train,y_train)
#預測X_test
predict_list = clf.predict(X_test)
#預測精度
precition = clf.score(X_test,y_test)
print('precition is : ',precition*100,"%")
#獲取模型返回值
n_Support_vector = clf.n_support_#支援向量個數
print("支援向量個數為: ",n_Support_vector)
Support_vector_index = clf.support_#支援向量索引
plot_point(dataArr,labelArr,Support_vector_index)這裡採用交叉驗證和rbf高斯核函式,對線性不可分資料進行預測,訓練集與測試集劃分比例為0.8:0.2
clf.predict:給定資料集,預測資料集類別
clf.score:給予訓練集與訓練集標籤獲取預測精度
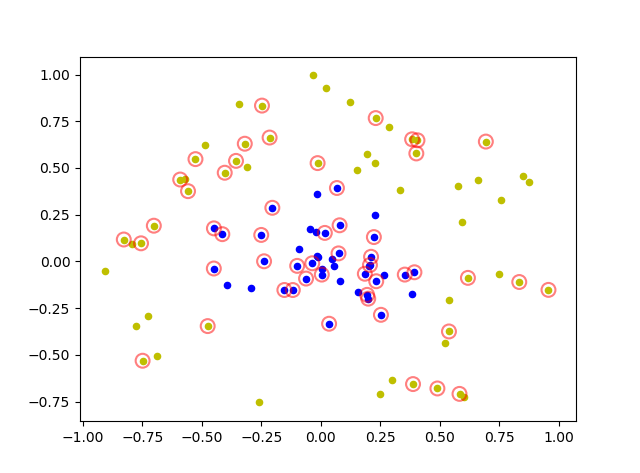
4)執行結果
precition is : 100.0 %
支援向量個數為: [27 26]
[Finished in 3.8s]精度為100%,支援向量共53個,一邊27個,一邊26個支援向量.
總結:
這裡精度達到100%,說明分類效果不錯,不過一般情況下不會出現100%的預測精度,這裡只是簡單的介紹了二維線性可分和二維線性不可分資料集,對於更高維的資料,支援向量機也總能發揮出比較好的效能,可以改造load_data函式實現資料讀取然後用svm預測,而對於多分類問題,可以使用整合學習,構建多個支援向量分類器提高效能,一般預設先使用rbf高斯核,然後再嘗試其他核函式,用交叉驗證法評價分類效果.SVM相關就先寫到這,這裡只寫了8篇,但對於支援向量機而言,可能80篇也寫不完,所以還有更多的知識需要學習探索~