NOIP專題複習(三) 狀壓DP學習筆記
其實並不是三,已經走了很多專題了。
之後慢慢填坑吧。
我覺得學普通的DP已經救不了我了。
發覺似乎NOIP狀壓蠻裸的(flag立的飛起),於是學一波。
其實在下作為一隻蒟蒻,認為狀壓DP屬於很好理解但不太好寫的型別。
還是從經典例題互不侵犯開始。
luogu1896 互不侵犯
在N×N的棋盤裡面放K個國王,使他們互不攻擊,共有多少種擺放方案。國王能攻擊到它上下左右,以及左上左下右上右下八個方向上附近的各一個格子,共8個格子。
1 <=N <=9, 0 <= K <= N * N
在下大致將學習這道題做法步驟拆分如下。
1,資料範圍是識別狀壓DP的標誌。
這個資料範圍,一般來說是狀壓DP。
2,位運算是進行狀壓DP的主力武器。
很多教程都會直接講一下四個運算子是什麼意思,然後直接上程式碼。
在下覺得有點不太友好啊orz。畢竟大家都知道這是什麼意思,只是不會寫而已。
首先對於這道題,用到的位運算大致解析如下:
假設現在某一行狀態為i,i的對應的二進位制數,某一位是1表示這一位放棋子,是0表示不放。
那麼分別來看這樣幾種情況:
1)左右相鄰
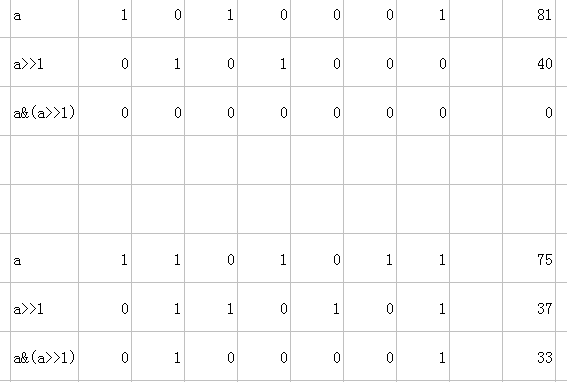
如圖,這裡舉了兩個例子,分別沒有左右相鄰和有相鄰的情況。顯而易見的,如果a&(a>>1)=0,就表示這一種方法是合法的,否則就不合法。
2)上下相鄰
這個還是蠻好理解的。如果a&b=0,就表示狀態a的每一位都和下一位都不衝突。
3)對角相接
>>1的本身含義就是將所有位向右移。那麼如果a,b對角線上是相接的,我們發現:
(a>>1) & b = 0表示不在右下方,(a<<1) & b表示不在左下方。
例如:
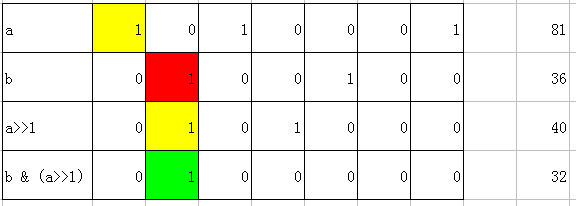
我們看到,黃色的在位運算之後與紅色的產生了衝突,不合法了。
4)判斷有多少放過
接下來還要用到統計某一行一共放過多少王的小函式。這一函式的實現原理很簡單:
while( x不為0 )
x右移一位
if(現在末位是1)
數量+1
end if
end while而末位是1可以用x & 1快速解決。
但這樣是比較慢的。有一個黑科技:lowbit(x) = x & (-x) ,這個東西可以取出二進位制下第一位不為0的數,原理各位請去查樹狀陣列。那麼這個程式碼可以這麼寫:
while(x不為0)
數量+1
x -= lowbit(x)
end while親測可以把8ms變成4ms。
3,行之間轉移是狀壓DP的本質
有了這些基礎,接下來就方便理解很多。
轉移方程:
這一狀態維護的是第i行放了j個王,狀態為s所得到的方案數之和。
實現上,我們可以遍歷維護每一種狀態,這樣複雜度
再來想想能不能簡化一些列舉次數——當然是可以的。
如果樸素演算法的話,我們需要首先判斷每一種狀態是否左右相鄰,這實際上是一種非常浪費的行為,那麼我們就可以加一次預處理,枚舉出所有符合條件可以轉化的狀態,同時處理出其數量.
那麼經過預處理的東西就是所有可能的狀態數。由此,我們可以寫出其預處理:
總複雜度
最後的問題就是一共有多少可能的狀態,顯然是
AC程式碼:
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <vector>
#include <queue>
using namespace std;
typedef long long LL;
#define INF 1<<8-1
LL n, m;
LL con[103], many[103], cnt;
LL dp[10][90][103], ans;
LL getnum(LL x) {
int qwq = 0;
while(x != 0) {
++qwq;
x = x - (x & (-x));
}
return qwq;
}
bool check(LL a, LL b) {
if(a & b) return 1;
if((a >> 1) & b) return 1;
if((a << 1) & b) return 1;
return 0;
}
int main() {
scanf("%d%d", &n, &m);
for(LL i = 0; i <= (1 << n) - 1; ++i) {
if((i & (i >> 1)) == 0) {
++cnt;
con[cnt] = i;
many[cnt] = getnum(i);
}
}
LL s, o, sl;
for(int i = 1; i <= cnt; ++i) dp[1][many[i]][i] = 1;
for(int i = 2; i <= n; ++i) {
for(int j = 0; j <= m; ++j) {
for(int k = 1; k <= cnt; ++k) {
s = con[k]; sl = many[k];
if(sl > j) continue;
for(int l = 1; l <= cnt; ++l) {
o = con[l];
if(check(s, o)) continue;
dp[i][j][k] += dp[i-1][j-sl][l];
}
}
}
}
for(int i = 1; i <= cnt; ++i) ans += dp[n][m][i];
cout<<ans<<endl;
return 0;
}luogu1789 玉米田
套路性很強的,來看玉米田。
資料範圍->12,狀壓,別猶豫。
再來看轉移,這題似乎比互不侵犯還要簡單一些,因為沒有數量限制。
因此這裡的狀態可以直接設為dp[i][s]表示第i行狀態為s,那麼
注意一點,不能放的限制條件我們用這個東西維護:
canput[i] = (canput[i] << 1) | (can ^ 1) 它表示第i行符合條件時的狀態,而每一位為1代表這一位不能放,以方便我們的&操作。
|可以方便的加上一個東西。
#include <iostream>
#include <algorithm>
#include <cstdio>
using namespace std;
typedef long long LL;
#define mod 100000000
LL n, m;
LL con[2003], many[2003], cnt;
LL dp[15][2003], ans;
inline LL lowbit(LL x) {
return x & (-x);
}
inline LL check(LL o, LL s) {
if(o & s) return 1;
else return 0;
}
LL canput[15];
int main() {
scanf("%d %d", &n, &m);
int can;
LL inf = (1 << m) - 1;
for(int i = 1; i <= n; ++i) {
canput[i] = 0;
for(int j = 1; j <= m; ++j) {
scanf("%d", &can);
canput[i] = (canput[i] << 1) | (can ^ 1);
}
}
for(LL i = 0; i <= inf; ++i) {
if((i & (i >> 1)) == 0)
++cnt, con[cnt] = i;
}
int len;
for(int i = 1; i <= cnt; ++i) {
if(con[i] & canput[1]) continue;
dp[1][i] = 1;
}
for(int i = 2; i <= n; ++i) {
for(int k = 1; k <= cnt; ++k) {
LL s = con[k];
if(s & canput[i]) continue;
for(int l = 1; l <= cnt; ++l) {
LL o = con[l];
if(o & canput[i - 1]) continue;
if(check(o, s)) continue;
dp[i][k] += dp[i-1][l];
}
}
}
for(int i = 1; i <= cnt; ++i) {
ans = (ans + dp[n][i]) % mod;
}
cout<<ans<<endl;
return 0;
}以上兩道題揭示了這類擺放問題的基本套路:先列舉預處理,然後判斷符合條件逐層轉移。現在來思考這一經典問題的兩種變形
1)如果現在要求相鄰空出來的數量為2怎麼辦?
每次轉移的時候加一層判斷,判斷上上行是否滿足,而預處理稍微加一點變化即可。
2)最優化,一個棋盤最多能放多少?
可以這麼寫:
luogu2883/NOIP2016D2T3 憤怒的小鳥
先和我默唸:辣雞憤怒的小鳥,毀我青春,毀我人蔘!
這個題資料範圍有一個m是用來給暴力選手的,可以無視(並不)
這是一道長的不像我們剛才看到的狀態壓縮題的狀壓題,其轉移方程很有趣:
換句話說,就是選取最小的集合進行轉移。
那麼這道題就可以分成這麼幾個部分:
1)列舉每個集合並儲存之
2)對於每種情況進行狀態壓縮搞
對於1,我們開一個query[i][j]陣列維護包含ij兩個點達到的值
對於2,注意兩件事:一個是每次轉移狀態可以只對第一頭沒有打死的豬進行討論,這樣是沒有後效性的,因為這頭豬遲早要被打死;另一個是我們需要討論對這一狀態轉移是單獨打這一頭還是連帶打一堆。
這道題集合的處理也是夠噁心的。首先我們用一個set[i][j]陣列維護過ij兩點的集合可以經過的小鳥,這裡要先解個方程。但這道題的坑點是,因為是拋體運動,a一定小於0,並且由於重力的影響,小鳥是不可能做直線運動的。
調了4個小時終於A了,真絕望。
#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
#include <bitset>
using namespace std;
typedef double db;
typedef long long LL;
#define EPS 0.0000001
#define INF 1<<20
LL dp[INF], set[20][20];
db torix[20], toriy[20];
int n, qinli;
bool equal(db a, db b) {
return fabs(a - b) < EPS;
}
inline bool getab(db x1, db y1, db x2, db y2, db &a, db &b) {
if(equal(x1, 0) && (!equal(x2, 0))) b = 0, a = y2 / (x2 * x2);
else if(equal(x2, 0) && (!equal(x1, 0))) b = 0, a = y1 / (x1 * x1);
else if(equal(x1, 0) && equal(x2, 0)) return false;
else {
a = (y1*x2-x1*y2)/(x1-x2)/x1/x2;
b = (y1-a*x1*x1) / x1;
if(a > 0) return false;
else if(a * b > 0) return false;
else return true;
}
}
inline bool isin (db a, db b, db x, db y) {
return equal(a * x * x + b * x , y);
}
void init() {
cin>>n>>qinli;
db atmp, btmp, ftmp;
LL now;
memset(set, 0, sizeof(set));
memset(dp, 0x3f, sizeof(dp));
for(int i = 1; i <= n; ++i) dp[i] = INF;
for(int i = 1; i <= n; ++i) cin>>torix[i]>>toriy[i];
for(int i = 1; i <= n; ++i)
for(int j = i + 1; j <= n; ++j) {
if(getab(torix[i], toriy[i], torix[j], toriy[j], atmp, btmp)) {
for(int t = 1; t <= n; ++t) {
if(isin(atmp, btmp, torix[t], toriy[t]))
set[i][j] |= (1<<(t - 1));
}
}
}
}
void work() {
LL s, o;
LL inf = (1 << n) - 1;
dp[0] = 0;
for(int i = 0; i <= inf; ++i) {
s = i, o = 1;
while(s & 1) s >>= 1, ++o;
dp[i | (1 << (o - 1))] = min(dp[i | (1 << (o - 1))], dp[i] + 1);
for(int j = o + 1; j <= n; ++j)
if(set[o][j])
dp[i | set[o][j]] = min(dp[i | set[o][j]], dp[i] + 1);
}
cout<<dp[(1 << n) - 1]<<endl;
}
int main() {
int T; cin>>T;
while(T--) {
init();
work();
}
}