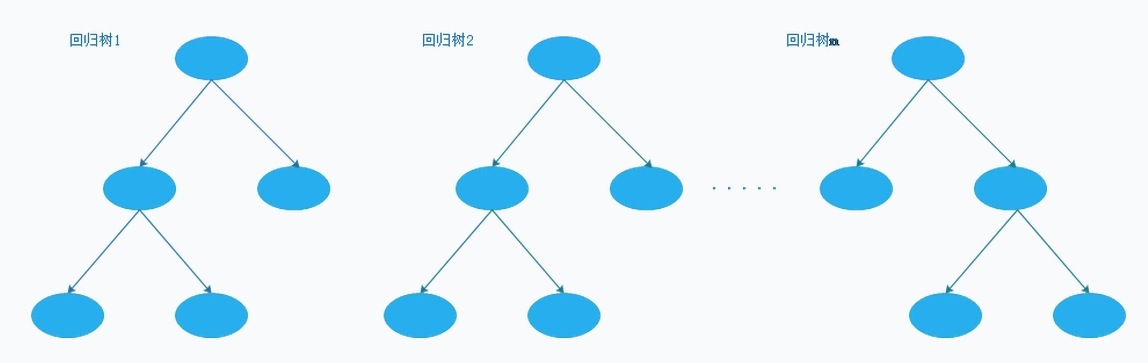
GBDT由一系列的迴歸樹組成，如下圖所示（樹的深度未必都要一樣，下圖僅為示意圖）。

GBDT原理

針對每一個類別訓練一系列的迴歸樹，再累加每個類別迴歸樹的預測值得到針對每個類別的最終的預測值。單獨拿一個類別來說，訓練的過程中假設需要預測的值為f(xi)，實際的值為yi，有Loss Function L(yi,f(xi))，f(xi)為引數。訓練的過程就是讓Loss Function最小化的過程。最小化可以通過梯度下降完成，令Loss Function對引數f(xi)求梯度有

那麼，只要引數f(xi)不斷往梯度方向變化，Loss Function就會減小直至收斂。即每一次迭代為

假設第一棵迴歸樹T1的預測值為f(xi)0，對這一時刻的引數f(xi)0求梯度，得到gf(x)0，因為梯度是根據訓練樣本中的實際值yi得到的，預測未知樣本時，並沒有實際的yi，因此需要估計這一時刻的梯度gf(x)0，這就需要通過第二棵迴歸樹來擬合。故利用根據訓練樣本求得的梯度值gf(x)0作為目標值，利用訓練樣本再訓練一棵迴歸樹T2，並用T2再求一遍梯度g′，之後更新引數得到f(xi)1。以此類推，迭代直到得到給定數目的迴歸樹。

此時這一系列的迴歸樹T1,T2,...,Tn的預測值累加後得到f(xi)n，可以令Loss Function足夠小，也就得到了一個訓練好的gbdt模型。

選取不同的Loss Function可以達到不同的目的，比如對於信用模型需要分類的情形，Loss Function為Deviance，對應的梯度為

pk表示樣本xi屬於第k個類別的概率，通過Softmax方法求得。因為有K個類別，所以得到K個系列的迴歸樹，每個系列最終的預測值分別為f1(x),f2(x),...,fK(X)，具體計算公式如下所示

GBDT的正則化

訓練的過程可以指定需要M棵迴歸樹，新的迴歸樹不斷擬合之前的殘差，在訓練集上的誤差可能逐漸變為0，導致過擬合。GBDT也有相應避免過擬合的方法。如
1. early stopping策略，保留一個驗證集，每增添一棵樹通過驗