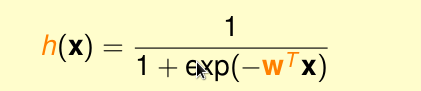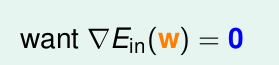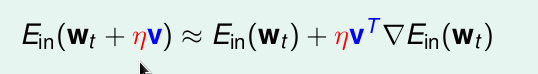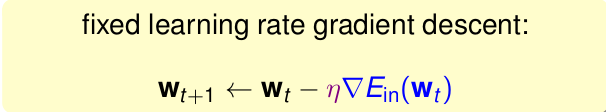logisitic 迴歸 +極大似然法 + 梯度下降法 (迭代優化)
logistic迴歸是分類問題。前面我們講的分類問題的輸出都是 “yes”或者“no”。但是在現實生活中,我們並不是總是希望結果那麼肯定,而是概率(發生的可能性)。比如,我們希望知道這個房子在第三個星期被賣出去的概率。那麼以前的分類演算法就無法使用了,這時logistic 迴歸就派上了用場。
也就是說,logistic 迴歸輸出的是一個概率值,而不是絕對的0/1。即目標函式變為
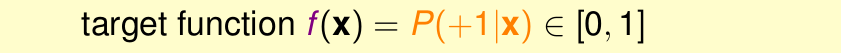
我們用logistic 迴歸做分類,結果輸出的是+1的概率。但是我們的樣本的y確是+1或者-1。打個比方,我們預測房子3個月後被賣出去的概率。
但是對於我們蒐集房子的樣本,只知道樣本3個月後是否成功被賣,並不知道該樣本被賣的概率。
也就是,我們的樣本的資料,不是這樣
而是這樣

logistic 迴歸
對於樣本x的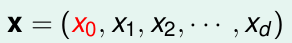
這d個特徵(還有一個偏移
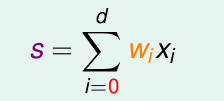
這個s的取值範圍是( 負無窮 到 正無窮 )。只是logisitc 迴歸用了一個函式將他壓縮到 [0,1]之間。由於這個壓縮函式是 單調遞增的,所以結果並不影響。
這個函式就是
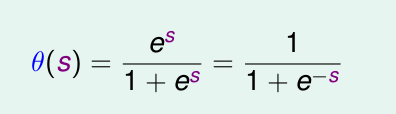
他是光滑且單調的。
那麼logistic 函式為
logistic 迴歸的Ein
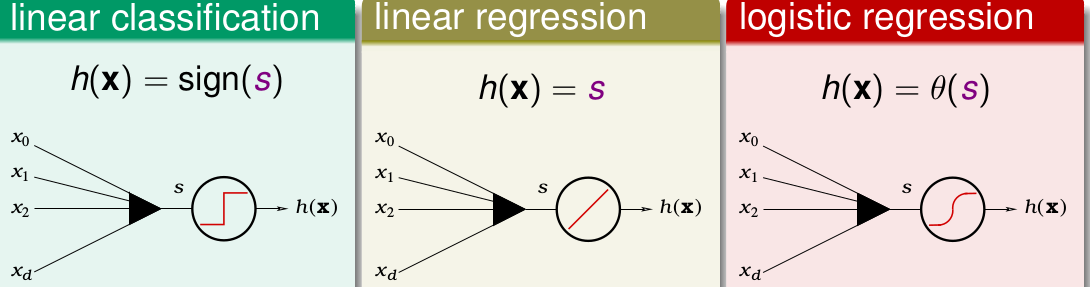
我們總共講了3種模型。線性分類,線性迴歸,logistic 迴歸。其實他們三者的核心都是
也就是都是 對特徵的加權再求和。
但是他們的h(x)和
對於h(x)的形式,三著分別為
對於
linear classfication 的
linear regression 的
而logistic迴歸又是什麼呢??現在我們來求一求
極大似然法
我們可得到

我們現在有一堆樣本
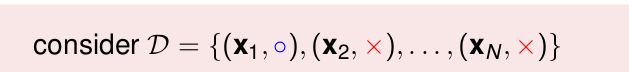
那麼他有f產生的概率為
我們有一個h ,h產生這堆樣本的概率為
極大自然法,如果h產生一模一樣的資料的概率 同 f產生這堆資料的概率越相近,那麼就可以說 上面h與f更加接近。
由於我們的樣本(資料)本就是f產生的,所以f產生這堆資料的概率很大,接近1。因此,我們希望h可以產生一模一樣的資料的概率接近1。
所以我們現在的目標是,
對於logistic迴歸,通過畫圖,我們可以得到關於他的對稱性
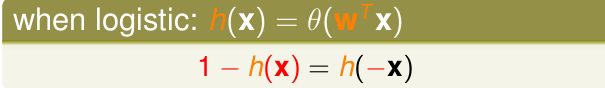
所以likelihood
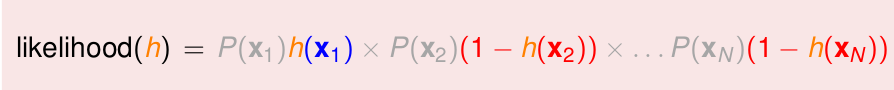
現在,可以改寫出
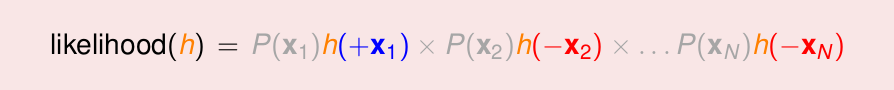
灰色的表示:由於我們相當於是再所有的h中找一個likelihood()最大的那個h,而對於所有的h,其
即問題轉化為

將其轉化為求w的形式
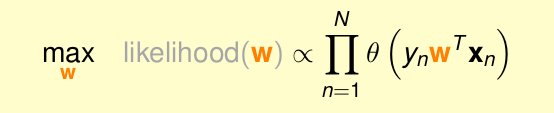
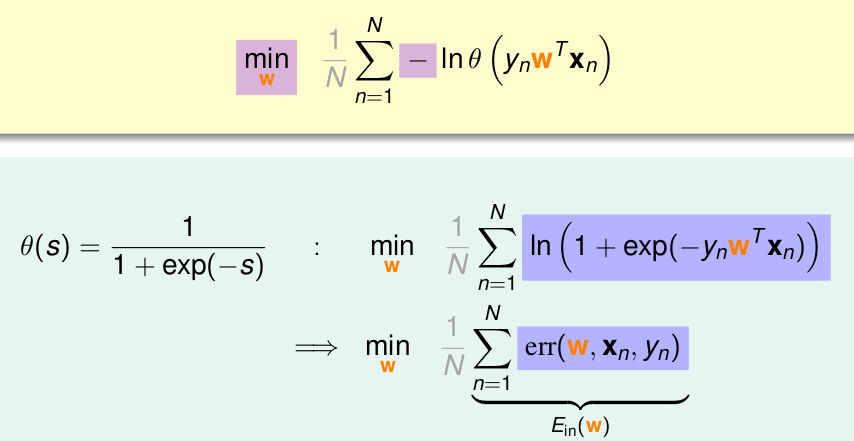
由於是乘積的形式,將其轉化為log形式
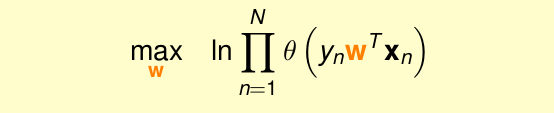
為了計算方便,將max轉化為min,並乘以
那麼我們的最終目標為
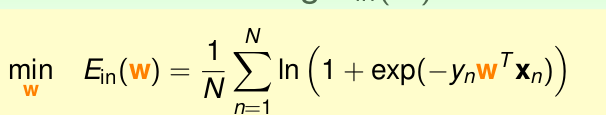
根據上面的式子,由於
梯度下降法

最後一步就是把所有的偏導彙總成一個式子。所以橘色的
最終變為
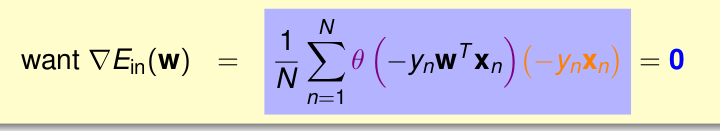
如果
我們回顧一下PLA演算法
其實上面兩步可以歸為1步

所以PLA演算法可以簡化為

發現,上面兩圖有兩個引數,
PLA通過不斷的迭代更新w的值,使得最終的值達到最優。這種演算法迭代優化方法。
logistic求解最小的
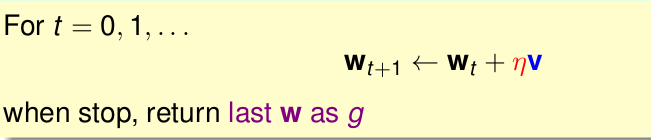
其中
那麼我們現在就通過求解正確的 步長
我們知道:
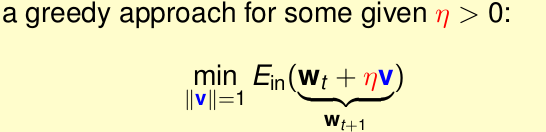
,以上為非線性的。當
根據泰勒公式:
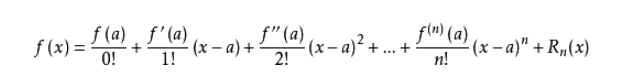
當
那麼問題就變為

我們想得到

這樣我們就求出了v的值。
即最終得到梯度下降為
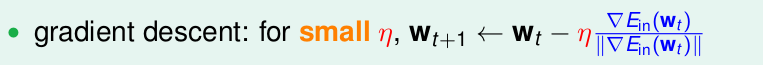
步長
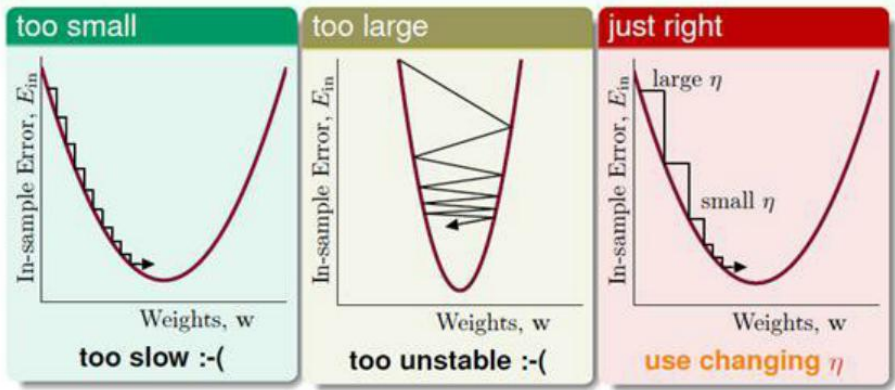
我們希望
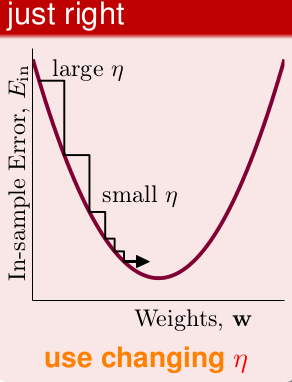
那麼其實希望
為了方便,這裡用正比,當然也可以用其他的。

最終結果為