前言

邏輯迴歸是分類當中極為常用的手段，因此，掌握其內在原理是非常必要的。我會爭取在本文中儘可能簡明地展現邏輯迴歸(logistic regression)的整個推導過程。

什麼是邏輯迴歸

邏輯迴歸在某些書中也被稱為對數機率迴歸，明明被叫做迴歸，卻用在了分類問題上，我個人認為這是因為邏輯迴歸用了和迴歸類似的方法來解決了分類問題。
假設有一個二分類問題，輸出為y∈{0,1}$y\in \{0,1\}$，而線性迴歸模型產生的預測值為z=wTx+b$z=w^{T}x+b$是實數值，我們希望有一個理想的階躍函式來幫我們實現z$z$值到0/1$0/1$值的轉化。

ϕ(z)=⎧⎩⎨00.51if z < 0if z = 0if z > 0

$\varphi (z)=\{\begin{array}{ll}0& \text{if z < 0}\\ 0.5& \text{if z = 0}\\ 1& \text{if z > 0}\end{array}$
然而該函式不連續，我們希望有一個單調可微的函式來供我們使用，於是便找到了Sigmoidfunction$Sigmoidfunction$來替代。
ϕ(z)=11+e−z$\varphi (z)={\displaystyle \frac{1}{1+e^{-z}}}$
兩者的影象如下圖所示（圖片出自文獻2）

圖1：sigmoid & step function
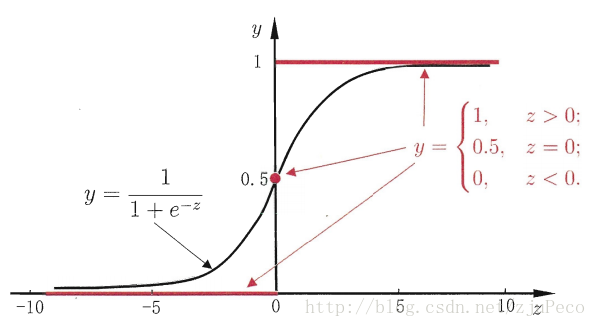
有了Sigmoidfuction$Sigmoidfuction$之後，由於其取值在[0,1]$[0,1]$，我們就可以將其視為類1$1$的後驗概率估計p(y=1|x)$p(y=1|x)$。說白了，就是如果有了一個測試點x$x$，那麼就可以用Sig

moidfuction$Sigmoidfuction$算出來的結果來當做該點x$x$屬於類別1$1$的概率大小。
於是，非常自然地，我們把Sigmoidfuction$Sigmoidfuction$計算得到的值大於等於0.5$0.5$的歸為類別1$1$，小於0.5$0.5$的歸為類別0$0$。
y^={10ifϕ(z)≥0.5otherwise$\hat{y}=\{\begin{array}{ll}1& if\varphi (z)\ge 0.5\\ 0& otherwise\end{array}$
同時邏輯迴歸與自適應線性網路非常相似，兩者的區別在於邏輯迴歸的啟用函式是Sigmoidfunction$Sigmoidfunction$而自適應線性網路的啟用函式是y=x$y=x$，兩者的網路結構如下圖所示（圖片出自文獻1）。

圖2：自適應線性網路

圖3：邏輯迴歸網路

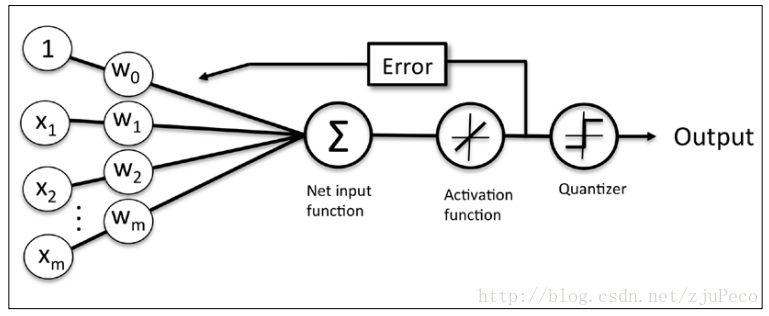
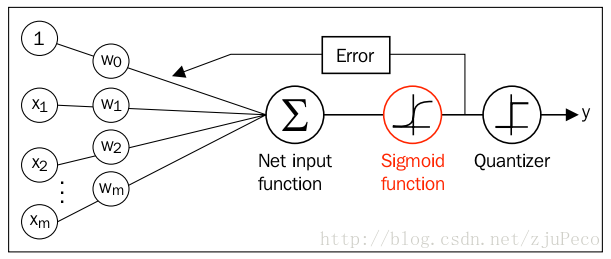
邏輯迴歸的代價函式

好了，所要用的幾個函式我們都有了，接下來要做的就是根據給定的訓練集，把引數w$w$給求出來了。要找引數w$w$，首先就是得把代價函式（cost function）給定義出來，也就是目標函式。
我們第一個想到的自然是模仿線性迴歸的做法，利用誤差平方和來當代價函式。

J(w)=∑i12(ϕ(z(i))−y(i))2$J(w)=\sum _i{\displaystyle \frac{1}{2}}(\varphi (z^{(i)})-y^{(i)}{)}^2$
其中，z(i)=wTx(i)+b$z^{(i)}=w^T{x}^{(i)}+b$，i$i$表示第i$i$個樣本點，y(i)$y^{(i)}$表示第