問題描述:

某售貨員要到若干城市去推銷商品，已知各城市之間的路程，他要選定一條從駐地出發，經過每個城市一遍，最後回到住地的路線，使總的路程最短。

演算法描述：

回溯法，序列樹， 假設起點為 1。

演算法開始時 x = [1, 2, 3, ..., n]

x[1 : n]有兩重含義 x[1 : i]代表前 i 步按順序走過的城市， x[i + 1 : n]代表還未經過的城市。利用Swap函式進行交換位置。

若當前搜尋的層次i = n 時，處在排列樹的葉節點的父節點上，此時演算法檢查圖G是否存在一條從頂點x[n-1] 到頂點x[n] 有一條邊，和從頂點x[n] 到頂點x[1] 也有一條邊。若這兩條邊都存在，則發現了一個旅行售貨員的迴路即：新旅行路線），演算法判斷這條迴路的費用是否優於已經找到的當前最優迴路的費用bestcost，若是，則更新當前最優值bestcost和當前最優解bestx。

若i < n 時，檢查x[i - 1]至x[i]之間是否存在一條邊, 若存在，則x [1 : i ] 構成了圖G的一條路徑，若路徑x[1: i] 的耗費小於當前最優解的耗費，則演算法進入排列樹下一層，否則剪掉相應的子樹。

程式碼實現：

#include <bits/stdc++.h>
using namespace std;
const int max_ = 0x3f3f3f;
const int NoEdge = -1;
int citynum;
int edgenum;
int currentcost;
int bestcost;
int Graph[100][100];
int x[100];
int bestx[100];
void InPut()
{
    int pos1, pos2, len;
    scanf("%d %d", &citynum, &edgenum);
    memset(Graph, NoEdge, sizeof(Graph));
    for(int i = 1; i <= edgenum; ++i)
    {
        scanf("%d %d %d", &pos1, &pos2, &len);
        Graph[pos1][pos2] = Graph[pos2][pos1] = len;
    }
}
void Initilize()
{
    currentcost = 0;
    bestcost = max_;
    for(int i = 1; i <= citynum; ++i)
    {
        x[i] = i;
    }
}
void Swap(int &a, int &b)
{
    int temp;
    temp = a;
    a = b;
    b = temp;
}
void BackTrack(int i) //這裡的i代表第i步去的城市而不是代號為i的城市

{
    if(i == citynum)
    {
        if(Graph[x[i - 1]][x[i]] != NoEdge && Graph[x[i]][x[1]] != NoEdge && (currentcost + Graph[x[i - 1]][x[i]] + Graph[x[i]][x[1]] < bestcost || bestcost == max_))
        {
            bestcost = currentcost + Graph[x[i - 1]][x[i]] + Graph[x[i]][x[1]];
            for(int j = 1; j <= citynum; ++j)
                bestx[j] = x[j];
        }
    }
    else
    {
        for(int j =  i; j <= citynum; ++j)
        {
            if(Graph[x[i - 1]][x[j]] != NoEdge && (currentcost + Graph[x[i - 1]][x[j]] < bestcost || bestcost == max_))
            {
                Swap(x[i], x[j]);  //這裡i 和 j的位置交換了, 所以下面的是currentcost += Graph[x[i - 1]][x[i]];
                currentcost += Graph[x[i - 1]][x[i]];
                BackTrack(i + 1);
                currentcost -= Graph[x[i - 1]][x[i]];
                Swap(x[i], x[j]);
            }
        }
    }
}
void OutPut()
{
    cout << "路線為:" << endl;
    for(int i = 1; i <= citynum; ++i)
        cout << bestx[i] << " ";
    cout << "1" << endl;
}
int main()
{
    InPut();
    Initilize();
    BackTrack(2);
    OutPut();
}

測試樣例：

輸入：

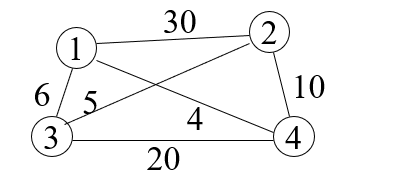
4 6
1 2 30
1 3 6
1 4 4
2 4 10
2 3 5

3 4 20

輸出：

路線為:

1 3 2 4 1

截圖：