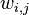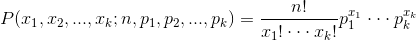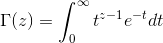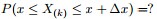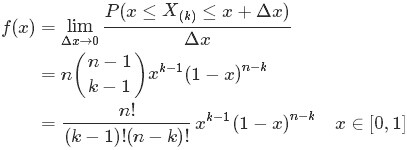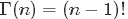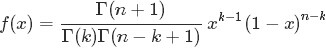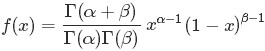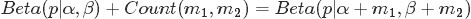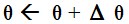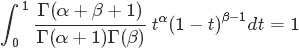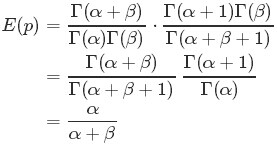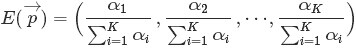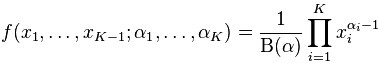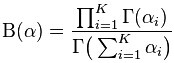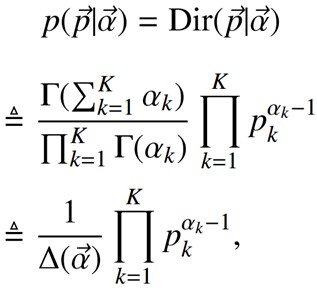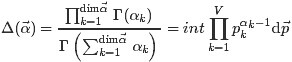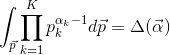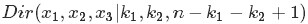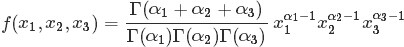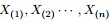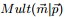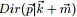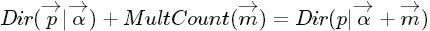通俗理解LDA主題模型
原文地址:http://blog.csdn.net/v_JULY_v/article/details/41209515
0 前言
印象中,最開始聽說“LDA”這個名詞,是緣於rickjin在2013年3月寫的一個LDA科普系列,叫LDA數學八卦,我當時一直想看來著,記得還列印過一次,但不知是因為這篇文件的前序鋪墊太長(現在才意識到這些“鋪墊”都是深刻理解LDA 的基礎,但如果沒有人幫助初學者提綱挈領、把握主次、理清思路,則很容易陷入LDA的細枝末節之中),還是因為其中的數學推導細節太多,導致一直沒有完整看完過。
2013年12月,在我組織的Machine Learning讀書會第8期上,@夏粉_百度 講機器學習中排序學習的理論和演算法研究,@沈醉2011 則講主題模型的理解。又一次碰到了主題模型,當時貌似只記得沈博講了一個汪峰寫歌詞的例子,依然沒有理解LDA到底是怎樣一個東西(但理解了LDA之後,再看沈博主題模型的
直到昨日下午,機器學習班 第12次課上,鄒講完LDA之後,才真正明白LDA原來是那麼一個東東!上完課後,趁熱打鐵,再次看LDA數學八卦,發現以前看不下去的文件再看時竟然一路都比較順暢,一口氣看完大部。看完大部後,思路清晰了,知道理解LDA,可以分為下述5個步驟:
- 一個函式:gamma函式
- 四個分佈:二項分佈、多項分佈、beta分佈、Dirichlet分佈
- 一個概念和一個理念:共軛先驗和貝葉斯框架
- 兩個模型:pLSA、LDA(在本文第4 部分闡述)
- 一個取樣:Gibbs取樣
本文便按照上述5個步驟來闡述,希望讀者看完本文後,能對LDA有個儘量清晰完整的瞭解。同時,本文基於鄒講LDA的
1 gamma函式
1.0 整體把握LDA
關於LDA有兩種含義,一種是線性判別分析(Linear Discriminant Analysis),一種是概率主題模型:隱含狄利克雷分佈(Latent Dirichlet Allocation,簡稱LDA),本文講後者。
另外,我先簡單說下LDA的整體思想,不然我怕你看了半天,鋪了太長的前奏,卻依然因沒見到LDA的影子而顯得“心浮氣躁”,導致不想再繼續看下去。所以,先給你吃一顆定心丸,明白整體框架後,咱們再一步步抽絲剝繭,展開來論述。
按照wiki上的介紹,LDA由Blei, David M.、Ng, Andrew Y.、Jordan於2003年提出,是一種主題模型,它可以將文件集 中每篇文件的主題以概率分佈的形式給出,從而通過分析一些文件抽取出它們的主題(分佈)出來後,便可以根據主題(分佈)進行主題聚類或文字分類。同時,它是一種典型的詞袋模型,即一篇文件是由一組詞構成,詞與詞之間沒有先後順序的關係。
此外,一篇文件可以包含多個主題,文件中每一個詞都由其中的一個主題生成。
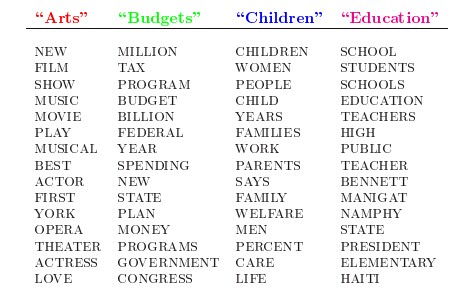
人類是怎麼生成文件的呢?LDA的這三位作者在原始論文中給了一個簡單的例子。比如假設事先給定了這幾個主題:Arts、Budgets、Children、Education,然後通過學習訓練,獲取每個主題Topic對應的詞語。如下圖所示:
然後以一定的概率選取上述某個主題,再以一定的概率選取那個主題下的某個單詞,不斷的重複這兩步,最終生成如下圖所示的一篇文章(其中不同顏色的詞語分別對應上圖中不同主題下的詞):
而當我們看到一篇文章後,往往喜歡推測這篇文章是如何生成的,我們可能會認為作者先確定這篇文章的幾個主題,然後圍繞這幾個主題遣詞造句,表達成文。 LDA就是要幹這事:根據給定的一篇文件,推測其主題分佈。 通俗來說,可以假定認為人類是根據上述文件生成過程寫成了各種各樣的文章,現在某小撮人想讓計算機利用LDA幹一件事:你計算機給我推測分析網路上各篇文章分別都寫了些啥主題,且各篇文章中各個主題出現的概率大小(主題分佈)是啥。 然,就是這麼一個看似普通的LDA,一度嚇退了不少想深入探究其內部原理的初學者。難在哪呢,難就難在LDA內部涉及到的數學知識點太多了。 在LDA模型中,一篇文件生成的方式如下:
- 從狄利克雷分佈
中取樣生成文件 i 的主題分佈
- 從主題的多項式分佈
中取樣生成文件i第 j 個詞的主題
- 從狄利克雷分佈
中取樣生成主題
對應的詞語分佈
- 從詞語的多項式分佈
中取樣最終生成詞語
其中,類似Beta分佈是二項式分佈的共軛先驗概率分佈,而狄利克雷分佈(Dirichlet分佈)是多項式分佈的共軛先驗概率分佈。
此外,LDA的圖模型結構如下圖所示(類似貝葉斯網路結構):
恩,不錯,短短6句話整體概括了整個LDA的主體思想!但也就是上面短短6句話,卻接連不斷或重複出現了二項分佈、多項式分佈、beta分佈、狄利克雷分佈(Dirichlet分佈)、共軛先驗概率分佈、取樣,那麼請問,這些都是啥呢?
這裡先簡單解釋下二項分佈、多項分佈、beta分佈、Dirichlet 分佈這4個分佈。
- 二項分佈(Binomial distribution)。
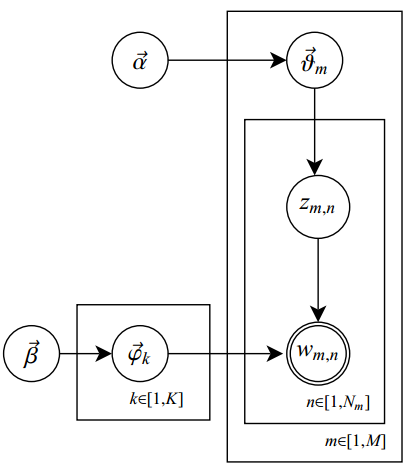
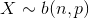 。簡言之,只做一次實驗,是伯努利分佈,重複做了n次,是二項分佈。二項分佈的概率密度函式為:
。簡言之,只做一次實驗,是伯努利分佈,重複做了n次,是二項分佈。二項分佈的概率密度函式為:
對於k = 0, 1, 2, ..., n,其中的
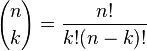 是二項式係數(這就是二項分佈的名稱的由來),又記為
是二項式係數(這就是二項分佈的名稱的由來),又記為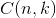 。回想起高中所學的那丁點概率知識了麼:想必你當年一定死記過這個二項式係數
。回想起高中所學的那丁點概率知識了麼:想必你當年一定死記過這個二項式係數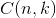 就是
就是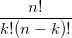 。
。
- 多項分佈,是二項分佈擴充套件到多維的情況。
多項分佈的概率密度函式為: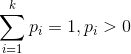
- Beta分佈,二項分佈的共軛先驗分佈。

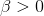 ,取值範圍為[0,1]的隨機變數
x 的概率密度函式
,取值範圍為[0,1]的隨機變數
x 的概率密度函式其中
注:,
。
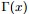 便是所謂的gamma函式,下文會具體闡述。
便是所謂的gamma函式,下文會具體闡述。
- Dirichlet分佈,是beta分佈在高維度上的推廣。
其中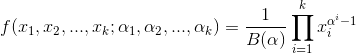
至此,我們可以看到二項分佈和多項分佈很相似,Beta分佈和Dirichlet 分佈很相似,而至於“Beta分佈是二項式分佈的共軛先驗概率分佈,而狄利克雷分佈(Dirichlet分佈)是多項式分佈的共軛先驗概率分佈”這點在下文中說明。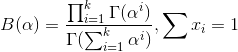
OK,接下來,咱們就按照本文開頭所說的思路:“一個函式:gamma函式,四個分佈:二項分佈、多項分佈、beta分佈、Dirichlet分佈,外加一個概念和一個理念:共軛先驗和貝葉斯框架,兩個模型:pLSA、LDA(文件-主題,主題-詞語),一個取樣:Gibbs取樣”一步步詳細闡述,爭取給讀者一個儘量清晰完整的LDA。
(當然,如果你不想深究背後的細節原理,只想整體把握LDA的主體思想,可直接跳到本文第4 部分,看完第4部分後,若還是想深究背後的細節原理,可再回到此處開始看)
1.1 gamma函式
咱們先來考慮一個問題(此問題1包括下文的問題2-問題4皆取材自LDA數學八卦):
- 問題1 隨機變數
- 把這n 個隨機變數排序後得到順序統計量
- 然後請問
的分佈是什麼。
為解決這個問題,可以嘗試計算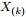
首先,把 [0,1] 區間分成三段 [0,x),[x,x+Δx],(x+Δx,1],然後考慮下簡單的情形:即假設n 個數中只有1個落在了區間 [x,x+Δx]內,由於這個區間內的數X(k)是第k大的,所以[0,x)中應該有 k−1 個數,(x+Δx,1] 這個區間中應該有n−k 個數。如下圖所示:
從而問題轉換為下述事件E: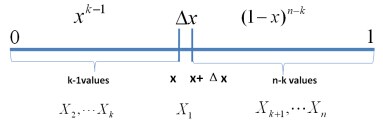
對於上述事件E,有: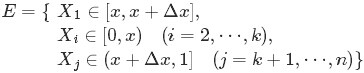
其中,o(Δx)表示Δx的高階無窮小。顯然,由於不同的排列組合,即n個數中有一個落在 [x,x+Δx]區間的有n種取法,餘下n−1個數中有k−1個落在[0,x)的有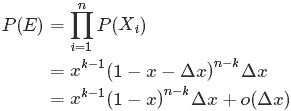
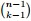 種組合,所以和事件E等價的事件一共有
種組合,所以和事件E等價的事件一共有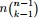 個。
如果有2個數落在區間[x,x+Δx]呢?如下圖所示:
個。
如果有2個數落在區間[x,x+Δx]呢?如下圖所示:
類似於事件E,對於2個數落在區間[x,x+Δx]的事件E’: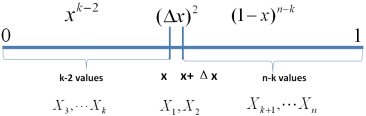
有: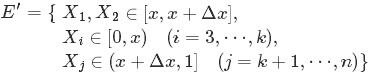
從上述的事件E、事件E‘中,可以看出,只要落在[x,x+Δx]內的數字超過一個,則對應的事件的概率就是 o(Δx)。於是乎有: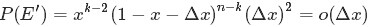
從而得到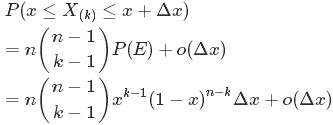
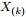 的概率密度函式
的概率密度函式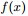 為:
為:
至此,本節開頭提出的問題得到解決。然仔細觀察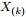
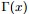
兩者結合是否會產生奇妙的效果呢?考慮到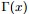
故將代入到
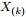
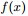
然後取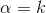
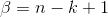
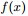
如果熟悉beta分佈的朋友,可能會驚呼:哇,竟然推出了beta分佈!
2 beta分佈
2.1 beta分佈
在概率論中,beta是指一組定義在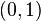 區間的連續概率分佈,有兩個引數
區間的連續概率分佈,有兩個引數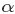 和
和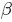 ,且
,且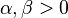 。
beta分佈的概率密度函式是:
。
beta分佈的概率密度函式是:
其中的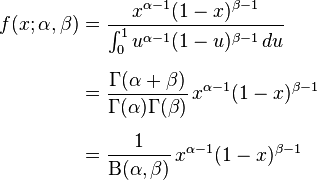
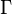 便是
便是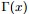 函式:
函式:
隨機變數X服從引數為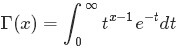
 的beta分佈通常寫作:
的beta分佈通常寫作: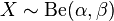 。
。
2.2 Beta-Binomial 共軛
回顧下1.1節開頭所提出的問題:“問題1 隨機變數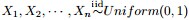 ,把這n 個隨機變數排序後得到順序統計量
,把這n 個隨機變數排序後得到順序統計量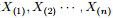 ,然後請問
,然後請問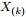 的分佈是什麼。” 如果,咱們要在這個問題的基礎上增加一些觀測資料,變成問題2:
的分佈是什麼。” 如果,咱們要在這個問題的基礎上增加一些觀測資料,變成問題2:
,對應的順序統計量是
,需要猜測
;
,
中有
個比p小,
個比
大;
- 那麼,請問
的分佈是什麼。
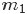 個比
個比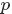 小,
小,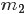 個比
個比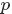 大”,換言之,Yi中有
大”,換言之,Yi中有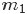 個比
個比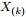 小,
小,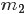 個比
個比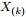 大,所以
大,所以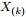 是
是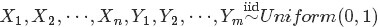 中第
中第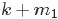 大的數。
根據1.1節最終得到的結論“只要落在[x,x+Δx]內的數字超過一個,則對應的事件的概率就是 o(Δx)”,繼而推出事件服從beta分佈,從而可知
大的數。
根據1.1節最終得到的結論“只要落在[x,x+Δx]內的數字超過一個,則對應的事件的概率就是 o(Δx)”,繼而推出事件服從beta分佈,從而可知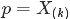 的概率密度函式為:
的概率密度函式為:
熟悉貝葉斯方法(不熟悉的沒事,參見此文第一部分)的朋友心裡估計又犯“嘀咕”了,這不就是貝葉斯式的思考過程麼?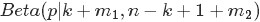
- 為了猜測
,在獲得一定的觀測資料前,我們對
的認知是:
,此稱為
的先驗分佈;
- 然後為了獲得這個結果“
中有
個比p小,
個比
大”,針對
是做了
次貝努利實驗,所以
服從二項分佈
;
- 在給定了來自資料提供的
的知識後,
的後驗分佈變為
。
- 先驗分佈
+ 樣本資訊
後驗分佈
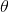 的認知是先驗分佈
的認知是先驗分佈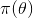 ,在得到新的樣本資訊
,在得到新的樣本資訊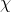 後,人們對
後,人們對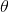 的認知為
的認知為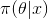 。
類比到現在這個問題上,我們也可以試著寫下:
。
類比到現在這個問題上,我們也可以試著寫下:
其中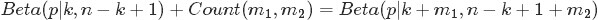
 對應的是二項分佈
對應的是二項分佈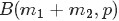 的計數。
更一般的,對於非負實數
的計數。
更一般的,對於非負實數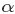 和
和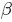 ,我們有如下關係
,我們有如下關係
針對於這種觀測到的資料符合二項分佈,引數的先驗分佈和後驗分佈都是Beta分佈的情況,就是Beta-Binomial共軛。換言之,Beta分佈是二項式分佈的共軛先驗概率分佈。
二項分佈和Beta分佈是共軛分佈意味著,如果我們為二項分佈的引數p選取的先驗分佈是Beta分佈,那麼以p為引數的二項分佈用貝葉斯估計得到的後驗分佈仍然服從Beta分佈。
此外,如何理解引數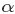 和
和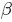 所表達的意義呢?
所表達的意義呢?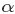 、
、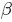 可以認為形狀引數,通俗但不嚴格的理解是,
可以認為形狀引數,通俗但不嚴格的理解是,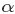 和
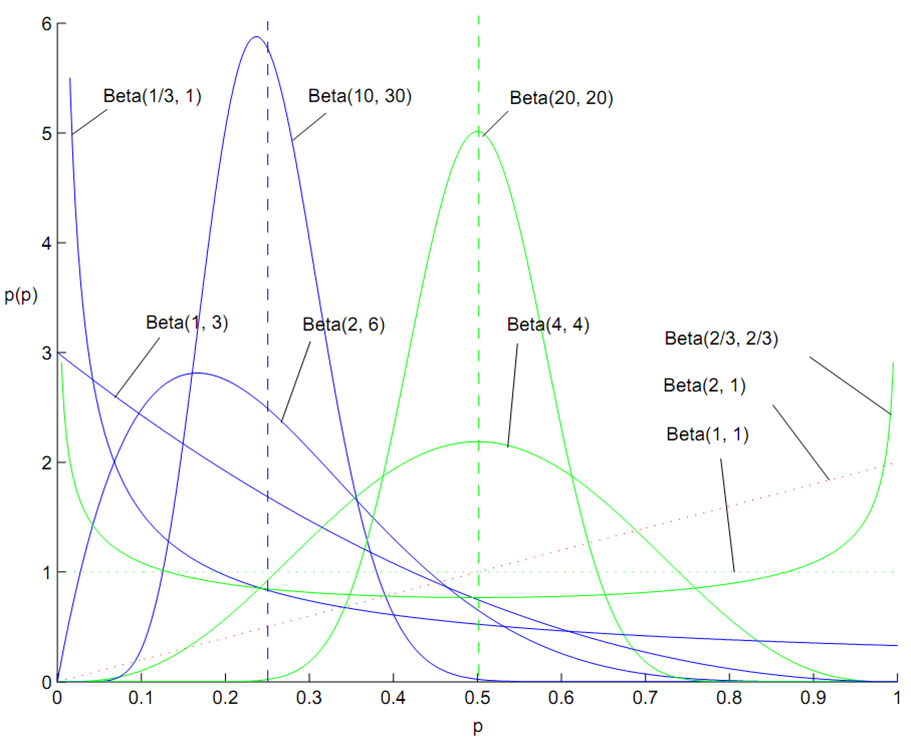
和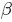 共同控制Beta分佈的函式“長的樣子”:形狀千奇百怪,高低胖瘦,如下圖所示:
共同控制Beta分佈的函式“長的樣子”:形狀千奇百怪,高低胖瘦,如下圖所示:
2.3 共軛先驗分佈
什麼又是共軛呢?軛的意思是束縛、控制,共軛從字面上理解,則是共同約束,或互相約束。 在貝葉斯概率理論中,如果後驗概率P(θ|x)和先驗概率p(θ)滿足同樣的分佈律,那麼,先驗分佈和後驗分佈被叫做共軛分佈,同時,先驗分佈叫做似然函式的共軛先驗分佈。 比如,某觀測資料服從概率分佈P(θ)時,當觀測到新的X資料時,我們一般會遇到如下問題:- 可否根據新觀測資料X,更新引數θ?
- 根據新觀測資料可以在多大程度上改變引數θ,即
- 當重新估計θ的時候,給出新引數值θ的新概率分佈,即P(θ|x)。
其中,P(x|θ)表示以預估θ為引數的x概率分佈,可以直接求得,P(θ)是已有原始的θ概率分佈。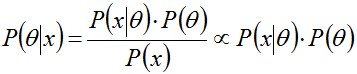
所以,如果我們選取P(x|θ)的共軛先驗作為P(θ)的分佈,那麼P(x|θ)乘以P(θ),然後歸一化的結果P(θ|x)跟和P(θ)的形式一樣。換句話說,先驗分佈是P(θ),後驗分佈是P(θ|x),先驗分佈跟後驗分佈同屬於一個分佈族,故稱該分佈族是θ的共軛先驗分佈(族)。 舉個例子。投擲一個非均勻硬幣,可以使用引數為θ的伯努利模型,θ為硬幣為正面的概率,那麼結果x的分佈形式為:
其共軛先驗為beta分佈,具有兩個引數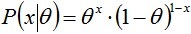
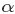 和
和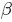 ,稱為超引數(hyperparameters)。且這兩個引數決定了θ引數,其Beta分佈形式為
,稱為超引數(hyperparameters)。且這兩個引數決定了θ引數,其Beta分佈形式為
然後計算後驗概率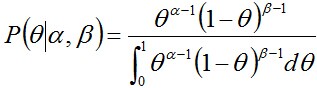
歸一化這個等式後會得到另一個Beta分佈,從而證明了Beta分佈確實是伯努利分佈的共軛先驗分佈。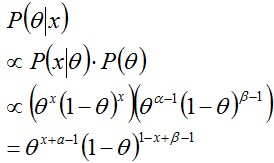
2.4 從beta分佈推廣到Dirichlet 分佈
接下來,咱們來考察beta分佈的一個性質。 如果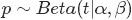 ,則有:
,則有:
注意到上式最後結果的右邊積分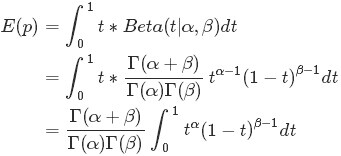
其類似於概率分佈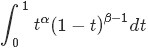
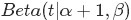 ,而對於這個分佈有
,而對於這個分佈有
從而求得
的結果為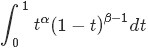
最後將此結果帶入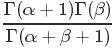
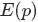 的計算式,得到:
的計算式,得到: 最後的這個結果意味著對於Beta 分佈的隨機變數,其均值(期望)可以用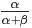
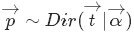
那什麼是Dirichlet 分佈呢?簡單的理解Dirichlet 分佈就是一組連續多變數概率分佈,是多變數普遍化的beta分佈。為了紀念德國數學家約翰·彼得·古斯塔夫·勒熱納·狄利克雷(Peter Gustav Lejeune Dirichlet)而命名。狄利克雷分佈常作為貝葉斯統計的先驗概率。
3 Dirichlet 分佈
3.1 Dirichlet 分佈
根據wikipedia上的介紹,維度K ≥ 2(x1,x2…xK-1維,共K個)的狄利克雷分佈在引數α1, ..., αK > 0上、基於歐幾里得空間RK-1裡的勒貝格測度有個概率密度函式,定義為:
其中,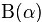
且
此外,x1+x2+…+xK-1+xK=1,x1,x2…xK-1>0,且在(K-1)維的單純形上,其他區域的概率密度為0。
當然,也可以如下定義Dirichlet 分佈
其中的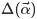
且根據Dirichlet分佈的積分為1(概率的基本性質),可以得到:
3.2 Dirichlet-Multinomial 共軛
下面,在2.2節問題2的基礎上繼續深入,引出問題3。
,
- 排序後對應的順序統計量
,
- 問
的聯合分佈是什麼?
從而有:
繼而得到於是我們得到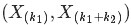
觀察上述式子的最終結果,可以看出上面這個分佈其實就是3維形式的 Dirichlet 分佈
令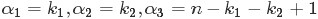
這個就是一般形式的3維 Dirichlet 分佈,即便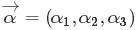
將Dirichlet分佈的概率密度函式取對數,繪製對稱Dirichlet分佈的影象如下圖所示(擷取自wikipedia上):
上圖中,取K=3,也就是有兩個獨立引數x1,x2,分別對應圖中的兩個座標軸,第三個引數始終滿足x3=1-x1-x2且α1=α2=α3=α,圖中反映的是引數α從α=(0.3, 0.3, 0.3)變化到(2.0, 2.0, 2.0)時的概率對數值的變化情況。
為了論證Dirichlet分佈是多項式分佈的共軛先驗概率分佈,下面咱們繼續在上述問題3的基礎上再進一步,提出問題4。
- 問題4
,排序後對應的順序統計量
- 令
,
,
(此處的p3非變數,只是為了表達方便),現在要猜測
;
,Yi中落到
,
,
三個區間的個數分別為 m1,m2,m3,m=m1+m2+m3;
- 問後驗分佈
的分佈是什麼。
為了方便討論,記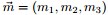
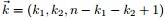
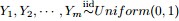
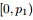
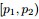
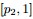
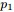
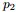
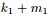
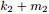
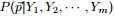
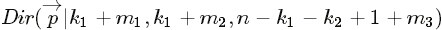
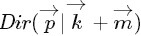
同樣的,按照貝葉斯推理的邏輯,可將上述過程整理如下:
- 我們要猜測引數
,其先驗分佈為
;
- 資料Yi落到三個區間
,
,
的個數分別為
,所以
服從多項分佈
- 在給定了來自資料提供的知識
後,
的後驗分佈變為
上述貝葉斯分析過程的直觀表述為:
令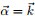
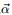
針對於這種觀測到的資料符合多項分佈,引數的先驗分佈和後驗分佈都是Dirichlet 分佈的情況,就是Dirichlet-Multinomial 共軛。換言之,至此已經證明了Dirichlet分佈的確就是多項式分佈的共軛先驗概率分佈。 意味著,如果我們為多項分佈的引數p選取的先驗分佈是Dirichlet分佈,那麼以p為引數的多項分佈用貝葉斯估計得到的後驗分佈仍然服從Dirichlet分佈。 進一步,一般形式的Dirichlet 分佈定義如下:
而對於給定的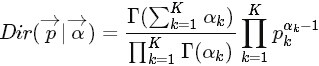
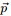 和
和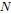 ,其多項分佈為:
,其多項分佈為:
結論是:Dirichlet分佈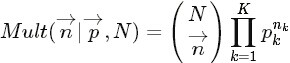
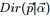 和多項分佈
和多項分佈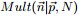 是共軛關係。
是共軛關係。
4 主題模型LDA
在開始下面的旅程之前,先來總結下我們目前所得到的最主要的幾個收穫:
- 通過上文的第2.2節,我們知道beta分佈是二項式分佈的共軛先驗概率分佈:
- “對於非負實數
和
,我們有如下關係
- “對於非負實數
其中
對應的是二項分佈
的計數。針對於這種觀測到的資料符合二項分佈,引數的先驗分佈和後驗分佈都是Beta分佈的情況,就是Beta-Binomial 共軛。”