先看到卷積運算，知道了卷積就是把模版與影象對應點相乘再相加，把最後的結果代替模版中心點的值的一種運算。但是，近來又看到了積分影象的定義，立馬暈菜，於是整理一番，追根溯源一下吧。

1 卷積影象

1.1 源頭

首先找到了一篇講解特別好的博文，原文為：卷積

貼過正文來看：

---------------------------------------------------------------------------------------------------------------

訊號處理中的一個重要運算是卷積.初學卷積的時候,往往是在連續的情形, 
　　兩個函式f(x),g(x)的卷積,是∫f(u)g(x-u)du 
　　當然，證明卷積的一些性質並不困難，比如交換，結合等等，但是對於卷積運算的來處，初學者就不甚了了。 
　　 
　　其實，從離散的情形看卷積，或許更加清楚， 
　　對於兩個序列f[n],g[n],一般可以將其卷積定義為s[x]= ∑f[k]g[x-k] 
　　 
　　卷積的一個典型例子,其實就是初中就學過的多項式相乘的運算, 
　　比如(x*x+3*x+2)(2*x+5) 
　　一般計算順序是這樣, 
　　(x*x+3*x+2)(2*x+5) 
　　= (x*x+3*x+2)*2*x+(x*x+3*x+2)*5 
　　= 2*x*x*x+3*2*x*x+2*2*x+ 5*x*x+3*5*x+10 
　　然後合併同類項的係數, 
　　2 x*x*x 
　　3*2+1*5 x*x 
　　2*2+3*5 x 
　　2*5 
　　---------- 
　　2*x*x*x+11*x*x+19*x+10 
　　 
　　實際上,從線性代數可以知道,多項式構成一個向量空間,其基底可選為 
　　{1,x,x*x,x*x*x,...} 
　　如此,則任何多項式均可與無窮維空間中的一個座標向量相對應, 
　　如,(x*x+3*x+2)對應於 
　　(1 3 2), 
　　(2*x+5)對應於 
　　(2,5). 
　　 
　　線性空間中沒有定義兩個向量間的卷積運算,而只有加法,數乘兩種運算,而實際上,多項式的乘法,就無法線上性空間中說明.可見線性空間的理論多麼侷限了. 
　　但如果按照我們上面對向量卷積的定義來處理座標向量, 
　　(1 3 2)*(2 5) 
　　則有 
　　2 3 1 
　　_ _ 2 5 
　　-------- 
　　    2 
　　 
　　 
　　2 3 1 
　　_ 2 5 
　　----- 
　　  6+5=11 
　　 
　　2 3 1 
　　2 5 
　　----- 
　　4+15 =19 
　　 
　　 
　　_ 2 3 1 
　　2 5 
　　------- 
　　  10 
　　 
　　 或者說, 
　　(1 3 2)*(2 5)=(2 11 19 10) 
　　 
　　回到多項式的表示上來, 
　　(x*x+3*x+2)(2*x+5)= 2*x*x*x+11*x*x+19*x+10 
　　 
　　似乎很神奇,結果跟我們用傳統辦法得到的是完全一樣的. 
　　換句話,多項式相乘,相當於係數向量的卷積. 

　　 
　　其實,琢磨一下,道理也很簡單, 
　　卷積運算實際上是分別求 x*x*x ,x*x,x,1的係數，也就是說，他把加法和求和雜合在一起做了。(傳統的辦法是先做乘法，然後在合併同類項的時候才作加法) 
　　以x*x的係數為例，得到x*x，或者是用x*x乘5，或者是用3x乘2x,也就是 
　　2 3 1 
　　_ 2 5 
　　----- 
　　 6+5=11 
　　其實,這正是向量的內積.如此則,卷積運算,可以看作是一串內積運算.既然是一串內積運算，則我們可以試圖用矩陣表示上述過程。 
　　 
　　[ 2 3 1 0 0 0] 
　　[ 0 2 3 1 0 0]==A 
　　[ 0 0 2 3 1 0] 
　　[ 0 0 0 2 3 1] 
　　 
　　[0 0 2 5 0 0]' == x 
　　 
　　b= Ax=[ 2 11 19 10]' 
　　 
　　採用行的觀點看Ax,則b的每行都是一個內積。 
　　A的每一行都是序列[2 3 1]的一個移動位置。 
　　 
　　--------- 
　　 
　　顯然,在這個特定的背景下,我們知道,卷積滿足交換,結合等定律,因為,眾所周知的,多項式的乘法滿足交換律,結合律.在一般情形下,其實也成立. 
　　 
　　在這裡,我們發現多項式,除了構成特定的線性空間外,基與基之間還存在某種特殊的聯絡,正是這種聯絡,給予多項式空間以特殊的性質. 
　　 
　　在學向量的時候，一般都會舉這個例子，甲有三個蘋果，5個橘子，乙有5個蘋果，三個橘子，則共有幾個蘋果，橘子。老師反覆告誡，橘子就是橘子，蘋果就是蘋果，可不能混在一起。所以有(3,5)+(5,3)=(8,8).是的，橘子和蘋果無論怎麼加，都不會出什麼問題的，但是，如果考慮橘子乘橘子，或者橘子乘蘋果，這問題就不大容易說清了。 
　　 
　　又如複數,如果僅僅定義複數為數對（a,b),僅僅線上性空間的層面看待C2,那就未免太簡單了。實際上，只要加上一條(a,b)*(c,d)=(ac-bd,ad+bc) 
　　則情況馬上改觀，複變函式的內容多麼豐富多彩，是眾所周知的。 
　　 
　　另外，回想訊號處理裡面的一條基本定理,頻率域的乘積,相當於時域或空域訊號的卷積.恰好跟這裡的情形完全對等.這後面存在什麼樣的隱態聯絡,需要繼續參詳. 
　　 
　　從這裡看,高等的卷積運算其實不過是一種初等的運算的抽象而已.中學學過的數學裡面，其實還蘊涵著許多高深的內容（比如交換代數）。溫故而知新,斯言不謬. 
　　 
　　其實這道理一點也不復雜，人類繁衍了多少萬年了，但過去n多年，人們只知道男女媾精，乃能繁衍後代。精子，卵子的發現，生殖機制的研究，也就是最近多少年的事情。 
　　 
　　孔子說，道在人倫日用中，看來我們應該多用審視的眼光看待周圍，乃至自身，才能知其然，而知其所以然。

---------------------------------------------------------------------------------------------------------------

從上文我們得知了卷積的來源。我們再找一下卷積的官方定義：數學中關於兩個函式的一種無窮積分運算。對於函式f1(t)和f2(t)，其卷積表示為：式中：“*”為卷積運算子號。

在泛函分析中，卷積(卷積)、旋積或摺積(英語：Convolution)是通過兩個函式f 和g 生成第三個函式的一種數學運算元，表徵函式f 與經過翻轉和平移與g 的重疊部分的累積。函式f與g的卷積記作f(t)*g(t)，它是其中一個函式翻轉並平移後與另一個函式的乘積的積分，是一個對平移量的函式。 

 函式f與g的卷積可以定義為： z(t)=f(t)*g(t)= ∫f(m)g(t-m)dm.

並且卷積定理指出：二個二維連續函式在空間域中的卷積可求其相應的二個傅立葉變換乘積的反變換而得。反之，在頻域中的卷積可用的在空間域中乘積的傅立葉變換而得。

其實，說了這麼多，我還是不太明白為什麼要對影象進行卷積，怎樣進行卷積。

1.2 卷積運算

提到卷積運算，首先離不開的就是卷積核，這個卷積核其實就是一個大小固定、由數值引數構成的陣列，陣列的參考點通常位於陣列的中心，陣列的大小稱為核支撐。單就技術而言，核支撐實際上僅僅由核數組的非0部分組成。或者，像其他說法，卷積核就是所謂的模板。

卷積運算，其實就是可看作是加權求和的過程，使用到的影象區域中的每個畫素分別與卷積核(權矩陣)的每個元素對應相乘，所有乘積之和作為區域中心畫素的新值。
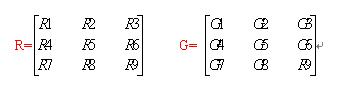
卷積示例：

  3 * 3 的畫素區域R與卷積核G的卷積運算：
              R5(中心畫素)=R1G1 + R2G2 + R3G3 + R4G4 + R5G5 + R6G6 + R7G7 + R8G8 + R9G9
            

如果對一幅影象進行卷積運算，可利用以陣列為中心為參考點的3*3卷積核。首先將核的參考點定位於影象的第一個畫素點，核的其餘元素覆蓋影象總其對應的區域性畫素點。對於每一個核點，我們可以得到這個點的值以及影象中對應影象點的值。將這些值相乘並求和，並將這個結果放在與輸入影象參考點所對應的位置。通過在整個影象上掃描卷積核，對影象的每個點重複此操作。最終可以得到影象的卷積影象。

當然，我們可以利用方程表示這個過程，定義影象為I(x,y),核為G（i,y）(其中0<i<Mi-1,0<j<Mj-1) 參考點位於（ai,aj）座標上，則卷積H(x,y)定義如下：

H(x,y) = sum[ I(x+i-ai,y+j-aj)G(i,j)].

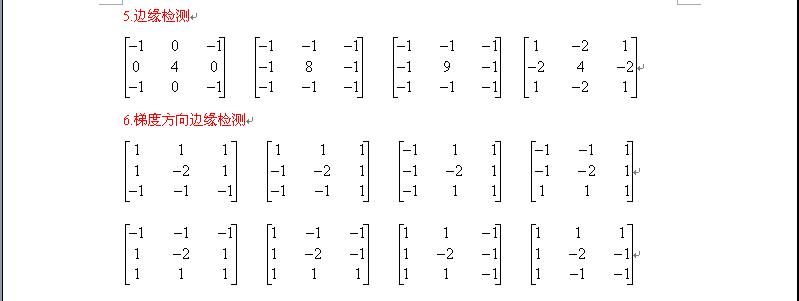
.常用模板（卷積核）

連續空間的卷積定義是 f(x)與g(x)的卷積是 f(t-x)g(x) 在t從負無窮到正無窮的積分值.t-x要在f(x)定義域內,所以看上去很大的積分實際上還是在一定範圍的.
實際的過程就是f(x) 先做一個Y軸的反轉,然後再沿X軸平移t就是f(t-x),然後再把g(x)拿來,兩者乘積的值再積分.想象一下如果g(x)或者f(x)是個單位的階越函式. 那麼就是f(t-x)與g(x)相交部分的面積.這就是卷積了.
把積分符號換成求和就是離散空間的卷積定義了.

1.3 意義

卷積是各種影象變換的基礎，一個特殊卷積所實現的功能是由其卷積核（模板）的形式決定的。高斯變換就是用高斯函式對影象進行卷積。

平滑處理：平滑型別：簡單模糊（對鄰域求和，並縮放），簡單無縮放變換的模糊（對鄰域求和），中值模糊（中值濾波），高斯模糊（高斯卷積），雙邊模糊（雙線性濾波）。

膨脹和腐蝕。

影象金字塔

拉普拉斯變換、canny運算元（求導數）

卷積性質：

1.卷積的符號表示式表明卷積是一種特殊型別的乘法，乘法某些代數性質可用於卷積。

    (1)commutative law：f₁(t)*f₂(t)=f₂(t)*f₁(t)
    (2)distributive law：f₁(t)*[f₂(t)+f₃(t)]=f₁(t)*f₂(t)+f₁(t)*f₃(t)
    (3)associative law：[f₁(t)*f₂(t)]*f₃(t)=f₁(t)*[f₂(t)*f₃(t)]
    (4)shift invariace：若f₁(t)*f₂(t)=f₃(t)，則f₁(t-t₀)*f₂(t)=f₁(t)*f₂(t-t₀)=f₃(t-t₀)
    此性質表明無論哪個函式平移了一個距離t₀,則所得的卷積就是簡單平移了同一距離，但大小和形狀保持不變。

2.卷積的微分和積分

    (1)兩函式相卷積後的導數等於兩函式之一的導數與另一函式相卷積。

    (2)兩函式相卷積後的積分等於兩函式之一的積分與另一函式相卷積。

    (3)推廣

    若f1(t)*f2(t) = s(t), 則，兩個分別為m階和n階函式導數卷積，由它們卷積的（m+n)階導數給出。

3.奇異訊號的卷積特性：

    (1)f(t)*δ(t)=f(t)    f(t)*δ(t-t₀)=f(t-t₀)   f(t-t₁)*δ(t-t₀)=f(t-t₀-t₁) 
    (2)δ(t)*δ(t)=δ(t)
    (3)f(t)*δ'(t)=f'(t)
    (4)
    推廣：f(t)*δ^(k)(t)=f^(k)(t)    f(t)*δ^(k)(t-t₀)=f^(k)(t-t₀)
    (5)f(t)*δ'(t)*u(t)=f'(t)*u(t)=f(t)    f(t)*δ''(t)*tu(t)=f''(t)*tu(t)=f(t)

所以，影象卷積與積分影象有什麼關係嗎？知者告知我啊。。。。。。

2 積分影象

surf演算法中要用到積分影象的概念。藉助積分影象，影象與高斯二階微分模板的濾波轉化為對積分影象的加減運算。積分影象（Integral Image）的概念是由viola和Jones提出來的，而將類似積分影象用於盒子濾波是由Simard等人提出。

積分影象中任意一點（i,j）的值為ii(i,j)為原影象左上角到任意點（i,j）相應的對角線區域灰度值的總和即：

公式中，I(x`,y`)表示原影象中點（i`,j`）的灰度值，ii（x,y）可以由下面兩公式迭代計算得到：

公式中，S（x,y）表示一列的積分，且S（i,-1）=0,ii(-1,j)=0.求積分影象，只需對原影象的所有畫素素進行一遍掃描。下面的程式碼為c++語言的實現

pOutImage[0][0] = pInImage[0][0];

for(int x = 1, x < nWidth; i++)
{
  pOutImage[x][0] = pInImage[x-1][0] + pInImage[x][0];

}

for(int y=1; y< nHeight ;y++)
{
  int nSum = 0;

  for(int x=0; x < nWidth;x++)
  {
    nSum = pInImage[x][y];

    pOutImage[x][y]= pInImage[x][y-1]+nSum;
  }

}

如圖表示，在求取視窗w內的像元灰度和時，不管視窗W的大小如何，均可利用積分影象的4個對應點（i1,j1）（i2,j2）（i3,j3）（i4,j4）的值計算的到。也就是說，求取視窗W內的像元灰度和與視窗的尺寸是無關的。視窗W內的像元的灰度和為

Sum（W）= ii(i4,j4) -ii(i2,j2) - ii(i3,j3) + ii(i1,j1)

下面看以截圖，相信都可以看懂

關於矩形區域內畫素點的求和應該是一種簡單重複性運算，採用這種思路總體上提高了效率。為什麼這麼說呢？假設一幅圖片共有n個畫素點，則計算n個位置的積分圖總共的加法運算有n-1次（注意：可不是次哦，要充分利用遞推思想），將這些結果儲存在一個跟原圖對應的矩陣M中。當需要計算影象中某個矩形區域內的所有畫素之和是直接像查表一樣，調出A,B,C,D四點的積分圖值，簡單的加減法（注意只需要三次哦）即可得到結果。反之，如果採用naive的方式直接在原影象中的某個矩形區域內求和，你想想，總共可能的矩形組合有多少？ ！！且對於一幅影象n那是相當大啊，所以2^n

 那可是天文數字，而且這裡面絕大部分的矩形有重疊，重疊意味著什麼？在算求和的時候有重複性的工作，其實我們是可以有效的利用已經計算過的資訊的。這就是積分圖法的內在思想：它實際上是先計算n個互不重疊（專業點說是不相交）的矩形區域內的畫素點求和，充分利用這些值（已有值）計算未知值，有點類似遞推的味道...這就完全避免了重複求和運算。

 這樣就可以進行2種運算：

    （1）任意矩形區域內畫素積分。由影象的積分圖可方便快速地計算影象中任意矩形內所有畫素灰度積分。如下圖2.3所示，點1的積分影象ii1的值為(其中Sum為求和) :

    ii1=Sum（A）

    同理，點2、點3、點4的積分影象分別為：

    ii2=Sum(A)+Sum(B);      ii3=Sum(A)+Sum(C);    ii4=Sum(A)+Sum(B)+Sum(C)+Sum(D);

    矩形區域D內的所有畫素灰度積分可由矩形端點的積分影象值得到:

                   Sum(D)=ii1+ii4-(ii2+ii3)            (1)

(2) 特徵值計算
    矩形特徵的特徵值是兩個不同的矩形區域畫素和之差，由(1)式可以計算任意矩形特徵的特徵值，下面以圖2.1中特徵原型A為例說明特徵值的計算。

    如圖2.4 所示，該特徵原型的特徵值定義為:

    Sum（A）-Sum（B）

    根據（1）式則有：Sum(A)=ii4+ii1-(ii2+ii3);    Sum(B)=ii6+ii3-(ii4+ii5);

   所以此類特徵原型的特徵值為:

                (ii4-ii3)-(ii2-ii1)+(ii4-ii3)-(ii6-ii5)

   另示：運用積分圖可以快速計算給定的矩形之所有象素值之和Sum(r)。假設r=(x,y,w,h),那麼此矩形內部所有元素之和等價於下面積分圖中下面這個式子:

                 Sum(r) = ii(x+w,y+h)+ii(x-1,y-1)-ii(x+w,y-1)-ii(x-1,y+h)

   由此可見，矩形特徵特徵值計算只與此特徵端點的積分圖有關，而與影象座標值無關。對於同一型別的矩形特徵，不管特徵的尺度和位置如何，特徵值的計算所耗費的時間都是常量，而且都只是簡單的加減運算。其它型別的特徵值計算方法類似。