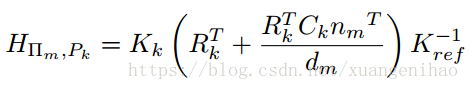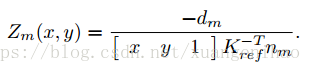平面掃描（plane-sweeping）介紹：

plane-sweeping演算法在三維重建中非常重要，其特別適合平行計算，因此通過GPU加速後可以使複雜的稠密重建達到實時。大多實時三維重建的深度圖生成部分採用plane-sweeping演算法。而且plane-sweeping不用rectify，甚至radial distortion的影象也可以用。研究semantic 3D的Christian Hane直接利用魚眼相機的影象planes-weeping也得到很好的效果。可以說plane-sweeping和patch-match為三維重建實時和非實時深度圖估計的主要演算法。
最初由《Multi-resolution real-time stereo on commodity graphics hardware》提出，後由《Real-time Plane-sweeping Stereo with Multiple Sweeping Directions》新增多面掃面用在實時三維重建中。本文也主要參考這兩篇文章。

演算法描述：

1、basic plane-sweeping algorithm

基本原理

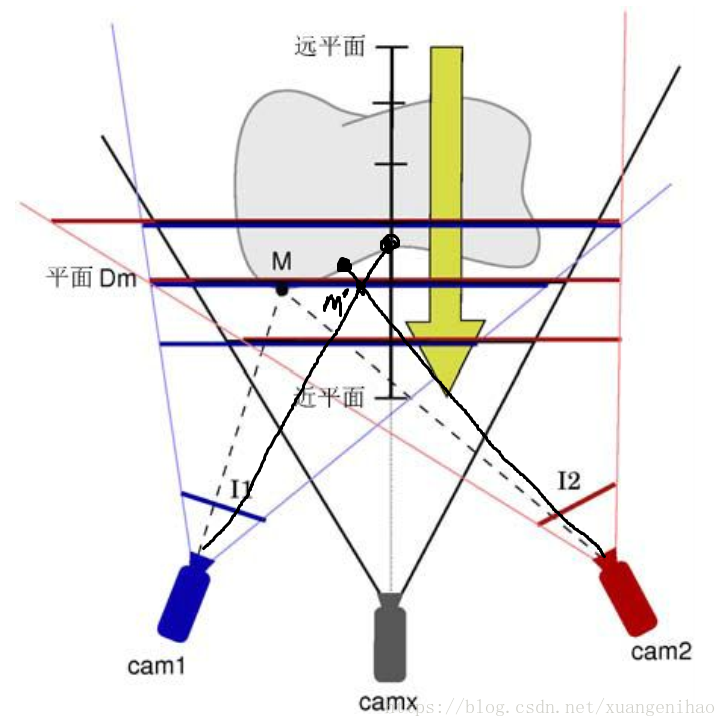
如下圖平面掃面演算法將深度範圍內分為一個個平面，深度範圍可以由很多方法獲得。如果平行平面足夠密集，空間被分割的足夠細，那麼，空間物體表面上的一點M 一定位於眾多平行平面中的其中一個平面 上，同時，所有能可以看到 M 的攝機看點 M 必然看到的是同一個顏色，也就是物體在點 M 本來的顏色。假設現在又有另一個點 M’，這個點也在一個平面上，假定如同 M 一樣也在 其平面上，但是他並不位於任何可見物體的表面上。這樣的點很有可能投影到每個可見攝像機上，並不是同樣的顏色（圖上兩個黑點）。

單應矩陣（homograph）

知道了基本原理後就是用數學建模。plane-sweeping利用平面與影象對應點的關係，因此採用Homography表述影象點之間的對映。

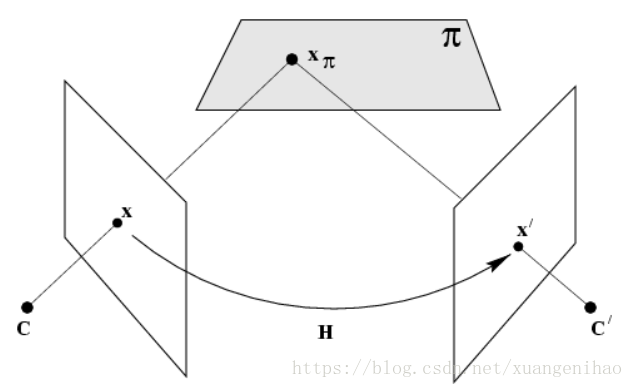
如上圖，若平面∏m=[nTm−d],m=1,2....M$\prod _m=[n_m^T-d],m=1,\mathrm{2....}M$，機投影矩陣為Pk=Kk[RTk−RTkCk],k=1,2...N$P_k=K_k[R_k^T-R_k^T{C}_k],k=1,\mathrm{2...}N$,Kk,R,T$K_k,R,T$ 分別是內參、旋轉和平移矩陣。參考影象Pref=Kk[I3×30]$P_{r}ef=K_k[I_3\times 30]$,那麼平面上一點在參考影象和影象 Pk$P_k$ 的投影點對應關係為：x′=Hx，H$x^{\prime }=Hx，H$ 即為Homograph：

Cost function

有了點之間的表述關係，接下來就是找到cost function對其優化。由於噪聲的影響，不能只利用兩點顏色相同，需利用改點的視窗資訊一塊進行比較因此cost function可以表述為：

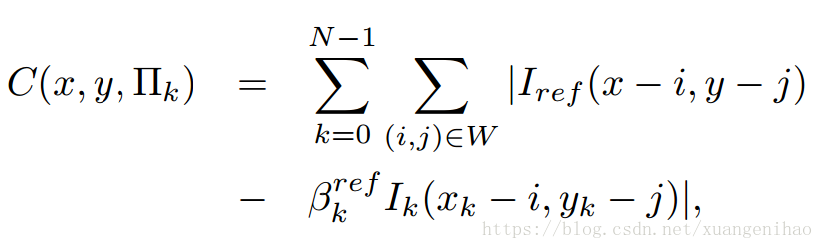
W$W$為以x,y為中心的視窗，$\beta為增益因子，計算光照變化後轉換為增益因子。
當然更具魯棒的聚合方法也可以用來生成cost，如：ZNCC等。在得到了cost function後只需計算個點最小值即為對應的平面：

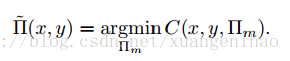
有了對應平面該點的深度如下計算：

2、Multiple Sweeping Directions

由於採用基於視窗的匹配方法，而視窗內畫素與中心畫素極有可能不在一個平面，因此利用上述方法會干擾中心畫素的匹配。
這裡也提一下《PatchMatch Stereo - Stereo Matching with Slanted Support Windows》這篇論文，這篇在patch match方法中比較出名。同樣解決原來基於視窗的匹配方法具有不連續性（大多呈階梯狀），這篇論文拋棄以前思想，用photo consistency直接估計視窗內平面方程，有了平面方程直接帶入該點座標即是深度值。後來北京自動化所的申抒含將其引入3d重建中《Accurate Multiple View 3D Reconstruction Using Patch-Based Stereo for Large-Scale Scenes》，該篇論文深度圖估計大體基於上篇，針對大規模三維重建做了修改，如：將平面法向量用球座標表示，影象間的畫素對映用homograph表示。由於不像雙目只有兩幅影象，3d重建中可以利用多影象進行深度圖融合，所以對上篇論文的深度估計做了三個簡化，以減小估計深度圖的時間。openmvs深度圖估計便是用的這篇論文方法，效果非常好。《Tanks and Temples: Benchmarking Large-Scale Scene Reconstruction》這個資料集對現有的三維重建開源演算法做了比較，目測openmvs比後起之秀colmap效果要好。但我在利用openmvs重建時，圖片過多總會出現錯誤，github也有人提問，作者貌似也無能為力。
以上幾種演算法其實思想相同，下圖一目瞭然。所以三維重建的深度圖估計無論實時還是非實時其實主要演算法相同。

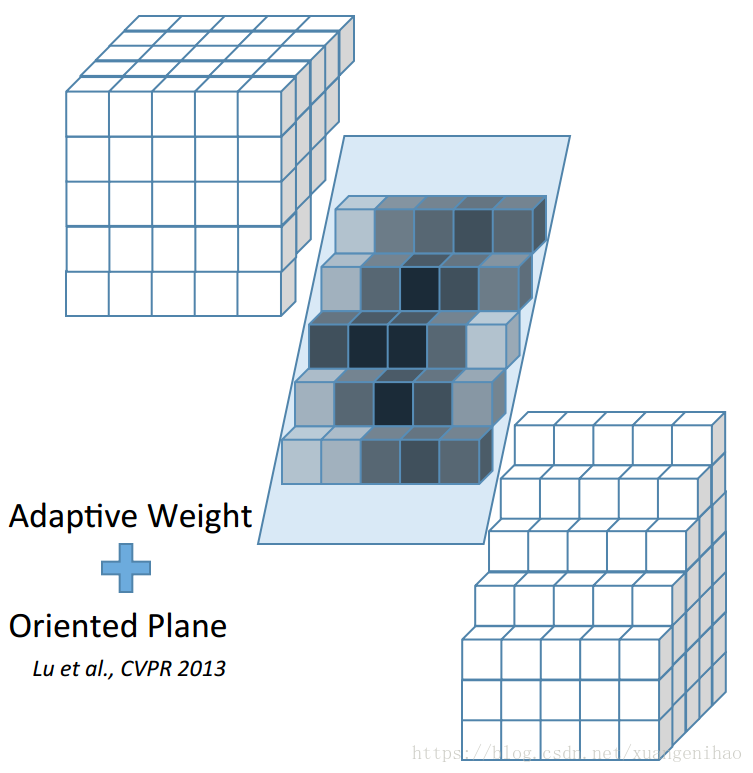
思想搞明白了講Multiple Sweeping Directions也簡單了，無非就是求取平面方程的方法不同。Multiple Sweeping Directions主要是基於房子都是方方正正的假設，如下圖（原論文沒給圖，只好靈魂畫圖師親自來了）。

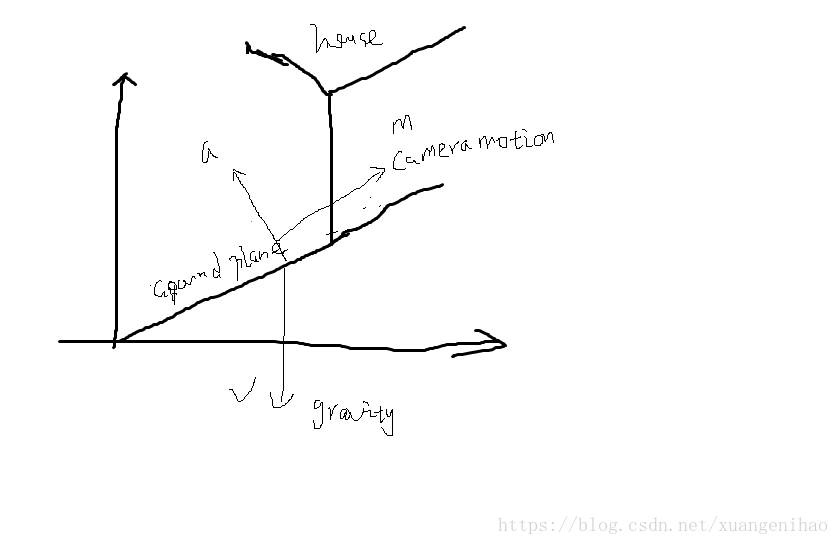
首先將從SFM獲得的三維點向重力方向投影至與重力正交的平面上，處於同一平面的三維點投影下去再一條直線上，直線間又是垂直關係，因此可以得到下面投影影象（a）。

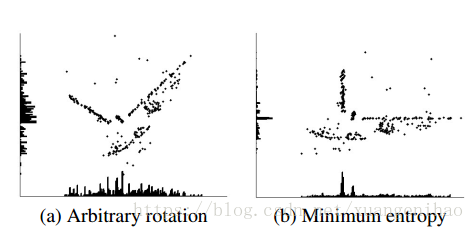
通過最小化資訊熵可以得到各平面的方向。得到平面方向只需按不同方向進行basic plane-sweeping即可。
參考文獻：

《Real-time Plane-sweeping Stereo with Multiple Sweeping Directions》
《A Space-Sweep Approach to True Multi-Image Matching》，plane sweeping開創性文章
colmap Dense 3D Geometry estimation
《PatchMatch Stereo - Stereo Matching with Slanted Support Windows》
《Accurate Multiple View 3D Reconstruction Using Patch-Based Stereo for Large-Scale Scenes》
《Semantic 3D Modeling from Images with Geometric Priors》
《多檢視立體匹配三維重建方法》