AC自動機演算法筆記
AC演算法是Alfred V.Aho(《編譯原理》(龍書)的作者),和Margaret J.Corasick於1974年提出(與KMP演算法同年)的一個經典的多模式匹配演算法,可以保證對於給定的長度為n的文字,和模式集合
AC演算法從某種程度上可以說是KMP演算法在多模式環境下的擴充套件。
KMP 演算法簡述
對於模式串而言,其字首,有可能也是模式串中的非字首的子串,而且這裡找的是最大字首,非字首可能包含多個字首。
在KMP演算法中有個陣列,叫做字首陣列,也有的叫next陣列,發現不匹配,下一步模式(pattern)串匹配目標(target)串的模式串的位置,它記錄著字串匹配過程中失配情況下,模式串可以向前跳幾個字元,當然它描述的也是子串的對稱程度,程度越高,值越大,當然之前可能出現再匹配的機會就更大。
示例1
| 序號 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| pattern | a | b | c | a | b | c | a | c | a | b |
| next | 0 | 0 | 0 | 1 | 2 | 3 | 4 | 0 | 1 | 2 |
示例2
| 序號 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| pattern | a | g | c | t | a | g | c | a | g | c | t | a | g | c | t | g |
| next | 0 | 0 | 0 | 0 | 1 | 2 | 3 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 4 | 0 |
示例2中,a g c t a g c,包含兩個字首。對於t,其next一定小於其前面c的next。
AC自動機演算法
AC are determined by three functions:goto function ,failure function,output function
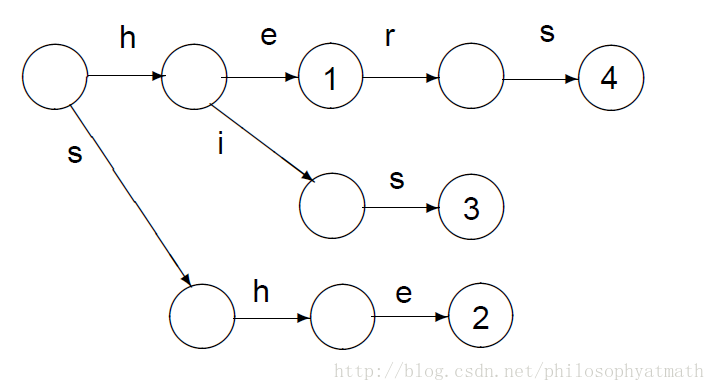
Keyword Tree
A keyword tree (or a trie ) for a set of patterns
- each edge of
K is labeled by a char acter - any two edges out of a node have diferent labels
Define the label of a nodev as the concatenation of edge labels on the path from the root tov , and denote it byL(v) - for each
p∈P there’s a nodev withL(v)=P , and - the label
L(v) of any leafv equals somep∈P
A keyword tree for
goto function
States: nodes of the keyword tree
initial state: 0 = the root
the goto function
- if edge
(q;v) is labeled bya , theng(q;a)=v ; g(0;a)=0 for each a that does not label an edge out of the root the automaton stays at the initial state while scanning non-matching characters- Otherwise
g(q;a)=∅ ;
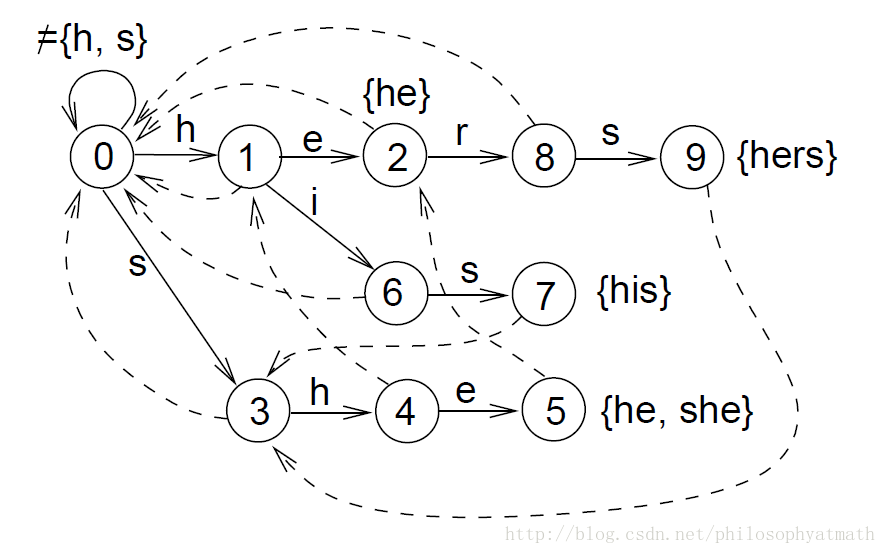
failure function
the failure function
f(q) is always defined, since
L(0)=ϵ is a prefix of any pattern
Dashed arrows are fail transitions
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|
| h- | e- | s- | h- | e- | i- | s- | r- | s- | |
| 0 | 0 | 0 | 1 | 2 | 0 | 3 | 0 | 3 |
output function
the output function
| 2 | {he} |
| 5 | {she,he} |
| 7 | {his} |
| 9 | {hers} |