編寫函式計算n的階乘(n
#include<iostream> using namespace std; int factorial(int a) { int result=1; for(int i=1;i<=a;i++) result*=i; return result; } int main() { int sum=0,n; cout<<"請輸入n的值"<<endl; cin>>n; for(int i=1;i<=n;i++) { sum+=factorial(i); } cout<<"n的階乘為:"<<sum<<endl; return 0; }
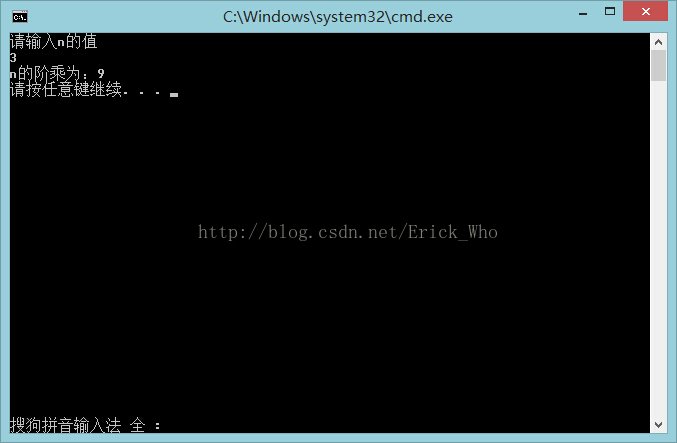
輸入的n為3時,執行結果如下:
相關推薦
求整數N階乘N!末尾有多少個0呢?
一、採用常規的做法,求出N的階乘,然後計算出該結果末尾的0的個數; 這種方法有兩個缺陷: (1)無論將結果定義為long還是double,結果值都會溢位; (2)效率低下; 方法一: 那麼我們
編寫函式計算n的階乘(n
#include<iostream> using namespace std; int factorial(int a) { int result=1; for(int i=1;i<=a;i++) result*=i; return result
(當N非常大時)巧用Java函式BigInteger計算N階乘
資料型別 型別名 位長 取值範圍 預設值 布林型 boolean 1 true,false false 位元組型 byte 8
lintcode入門級-計算出n階乘中尾部零的個數
題目地址:https://www.lintcode.com/problem/trailing-zeros/description 我想法很簡單,算出數值大小,直接對尾部進行除法取餘找0: (function () { var trailingZeros = function
【演算法】計算出n階乘中尾部零的個數
思路: 觀察1-20階乘的結果,觀察尾數為0的分佈情況 發現有一個5就會出現一個0 其中5!(有一個5),10!(有兩個5) 5!=120(一個0) 10!=3628800(兩個0) #include <stdio.h> long trailingZeros(long n) {
設計一個演算法,計算出n階乘中尾部零的個數
考慮到只要有5,或者因子為5的數,就可以產生0的尾部。假如1*2*3*4*...*250,那麼250/5=50可以知道,有50個為5的倍數,但是裡面有多少個為25的倍數,125的倍數..., 50/5=10,可知25的倍數有10個,10/5=2,可知125的倍數有兩個,以此
【Python】設計一個演算法,計算出n階乘中尾部零的個數
1.常見的思路:先求N的階乘,再計算零的個數。 (但是,時間消耗太大) def trailingZeros( n): S = 1 for i in range(1,n+1): S = S * i
計算n階乘中尾部0的個數
題目描述: 設計一個演算法,計算出n階乘中尾部零的個數。 eg. 11! = 39916800 輸入11,結果應該返回2。 分析: n的階乘可以分解為k和10的m次冪的乘積,結果resul
斯特林公式-Stirling公式(取N階乘近似值)-HDU1018-Big Number 牛客網NowCoder 2018年全國多校算法寒假訓練營練習比賽(第三場)A.不凡的夫夫
subject color content coder -m ria 一點 練習 java 最近一堆題目要補,一直鹹魚,補了一堆水題都沒必要寫題解。備忘一下這個公式。 Stirling公式的意義在於:當n足夠大時,n!計算起來十分困難,雖然有很多關於n!的等式,但並不能很
Java:演算法 - 求正整數階乘n!
數學公式:n!=1 * 2 * 3…(n-2) * (n-1) * n 應用方面:伽瑪函式與排列組合 遞迴實現程式碼: public static long fac(int n){ if(n == 0 || n ==1) return 1;
階乘n!的結尾後面有多少個零
LeetCode - 階乘後的零 思路:我們將 n! 進行質因數分解,使它由質數相乘得來,即 n!=2x×3y×5z×7w×...n!=2^x \times 3^y \times 5^z \times
Java怎樣求解n的階乘 n!(詳解)
n!是表示為自然數n的階乘,即:n!=1 × 2 × 3…(n-2) × (n-1) × n。如: 9!=9×8×7×6×5×4×3×2×1。 階乘也可以遞迴方式定義:0!=1,n!=(n-1)!×n。 希望對您有所幫助。 具體程式碼實現: import java.util.Sc
還是逆元之O(n)階乘逆元。。。
除草 做一個題發現了一個逆元的知識盲點,就是階乘的逆元 然後發現了可以這樣 fac[0]=fac[1]=1; for(int i=2;i<=MAXN;i++)fac[i]=fac[i-1]*i%mod; inv[MAXN]=quipow(fac[MAXN],mod-2
關於N的階乘(n!)的java演算法實現
很多公司面試都會有一個問題,就是求N階乘,主要是考查一些程式設計的基礎知識如迴圈、型別的最大長度、遞迴等。 例如最簡單的實現是: public void factorial(int n){ long result = 1; for(int i=0;i<n;i+
javascript實現n階乘的2個方法
方案一:利用while迴圈 function factorial(num){ var result = 1; while(num){ result *= num; num--; } return result; }方案二:利用函式遞迴 f
C++ 求n的階乘n!(n>0)
一、方法1:用迴圈 #include <iostream> using namespace std; int main(int argc, const char * argv[]) { int i, n, res; // res儲存積 &nb
求n階乘中尾部零的個數(JAVA)
描述 設計一個演算法,計算出n階乘中尾部零的個數 樣例 11! = 39916800,因此應該返回 2 挑戰 O(logN)的時間複雜度 所有可能造成尾部0的只有10的倍數,5的倍數,也就是求階乘中擁有的5的個數。 例如 11 = 1,2,3,4
n!階乘結尾有多少個零?
計算出n!結果後判斷是不行的,結果太大會溢位。正確思路應該是去判斷 n~1之間所有數的特點,這之間的所有數統稱為“子值”吧。 n!
n階乘後面0的個數+組合數學結果0的個數舉例+公式推導
先掛上一題,用作例子。 (n!%(10^k))==0. 已知n,求能使上式成立的k的最大值。 例如 5!= 120 有1個0,10!= 3628800 ,有2個0。 很明顯,階乘中所有數的因
斯特林公式 ——Stirling公式(取N階乘近似值)
斯特靈公式是一條用來取n階乘近似值的數學公式。一般來說,當n很大的時候,n階乘的計算量十分大,所以斯特靈公式十分好用。從圖中可以看出,即使在n很小的時候,斯特靈公式的取值已經十分準確。