Surf演算法學習心得(一)——演算法原理
阿新 • • 發佈:2019-01-30
Surf演算法是對Sift演算法的一種改進,主要是在演算法的執行效率上,比Sift演算法來講執行更快!由於我也是初學者,剛剛才開始研究這個演算法,然而網上對於Surf演算法的資料又尤為極少,稍微介紹的明白一點的還是英文。所以在此想借這個機會把我所理解的部分介紹一下,對於後面準備學習Surf演算法的朋友來說,希望有一點點的幫助!言歸正傳,心得大致包括幾下幾部分:
1、演算法原理;2、原始碼簡析;3、OpenCV中Demo分析;4、一些關於Surf演算法的剖析。
 (2)、特徵點過濾並進行精確定位;
(2)、特徵點過濾並進行精確定位;

(3)、為特徵點分配方向值;
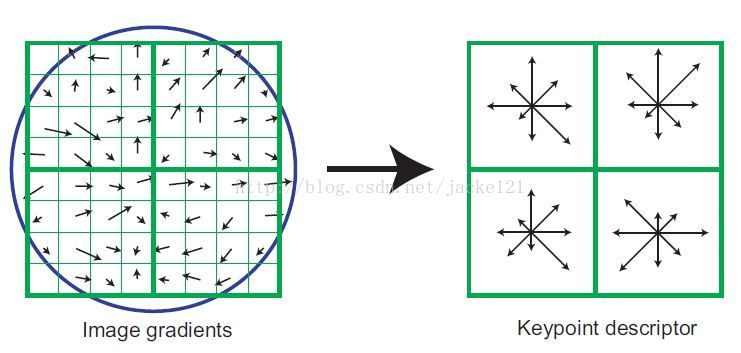
(4)、生成特徵描述子。 以特徵點為中心取16*16的鄰域作為取樣視窗,將取樣點與特徵點的相對方向通過高斯加權後歸入包含8個bin的方向直方圖,最後獲得4*4*8的128維特徵描述子。示意圖如下:
當兩幅影象的Sift特徵向量生成以後,下一步就可以採用關鍵點特徵向量的歐式距離來作為兩幅影象中關鍵點的相似性判定度量。取圖1的某個關鍵點,通過遍歷找到影象2中的距離最近的兩個關鍵點。在這兩個關鍵點中,如果次近距離除以最近距離小於某個闕值,則判定為一對匹配點。
2、Surf演算法原理
(1)、構建Hessian矩陣
Hessian矩陣是Surf演算法的核心,為了方便運算,假設函式f(z,y),Hessian矩陣H是由函式,偏導陣列成:
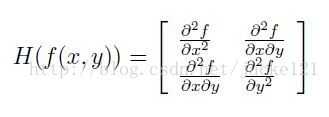
H矩陣判別式為: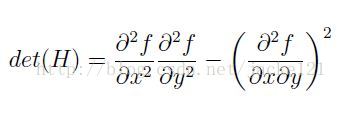
判別式的值是H矩陣的特徵值,可以利用判定結果的符號將所有點分類,根據判別式取值正負,來判別該點是或不是極值點。在SURF演算法中,用影象畫素l(x,y)代替函式值f(x,y),選用二階標準高斯函式作為濾波器,通過特定核間的卷積計算二階偏導數,這樣便能計算出H矩陣的三個矩陣元素L。、L。、k,從而計算出H矩陣:
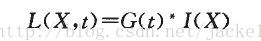
L。(X,£)是一幅影象在不同解析度下的表示,可以利用高斯核G(£)與影象函式,(X)在點X一(z,y)的卷積來實現,核函式G(£)具體表示如式(5),g(£)為高斯函式,t為高斯方差,L。與L。同理。通過這種方法可以為影象中每個畫素計算出其H行列式的決定值,並用這個值來判別特徵點。為方便應用,Herbert Bay提出用近似值現代替L。為平衡準確值與近似值間的誤差引入權值叫,權值硼隨尺度變化,則H矩陣判別式可表示為:
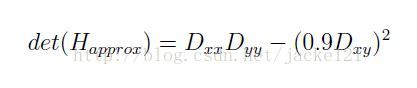
(2)、構建尺度空間 影象的尺度空間是這幅影象在不同解析度下的表示,由式(4)知,一幅影象j(X)在不同解析度下的表示可以利用高斯核G(£)的卷積來實現,影象的尺度大小一般用高斯標準差來表示[6]。在計算視覺領域,尺度空間被象徵性的表述為一個影象金字塔,其中,輸入影象函式反覆與高斯函式的核卷積並反覆對其進行二次抽樣,這種方法主要用於Sift演算法的實現,但每層影象依賴於前一層影象,並且影象需要重設尺寸,因此,這種計算方法運算量較大,而SURF演算法申請增加影象核的尺寸,這也是SIFT演算法與SURF演算法在使用金字塔原理方面的不同。演算法允許尺度空間多層影象同時被處理,不需對影象進行二次抽樣,從而提高演算法效能。圖1(a)是傳統方式建立一個如圖所示的金字塔結構,影象的寸是變化的,並且運(1) 算會反覆使用高斯函式對子層進行平滑處理,圖1(b)說明Surf演算法使原始影象保持不變而只改變濾波器大小。
(3)、精確定位特徵點 所有小於預設極值的取值都被丟棄,增加極值使檢測到的特徵點數量減少,最終只有幾個特徵最強點會被檢測出來。檢測過程中使用與該尺度層影象解析度相對應大小的濾波器進行檢測,以3×3的濾波器為例,該尺度層影象中9個畫素點之一圖2檢測特徵點與自身尺度層中其餘8個點和在其之上及之下的兩個尺度層9個點進行比較,共26個點,圖2中標記‘x’的畫素點的特徵值若大於周圍畫素則可確定該點為該區域的特徵點。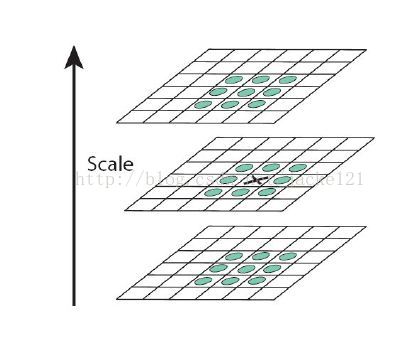
(4)、主方向確定 為保證旋轉不變性[8I,首先以特徵點為中心,計算半徑為6s(S為特徵點所在的尺度值)的鄰域內的點在z、y 方向的Haar小波(Haar小波邊長取4s)響應,並給這些響應值賦高斯權重係數,使得靠近特徵點的響應貢獻大,而遠離特徵點的響應貢獻小,其次將60。範圍內的響應相加以形成新的向量,遍歷整個圓形區域,選擇最長向量的方向為該特徵點的主方向。這樣,通過特徵點逐個進行計算,得到每一個特徵點的主方向。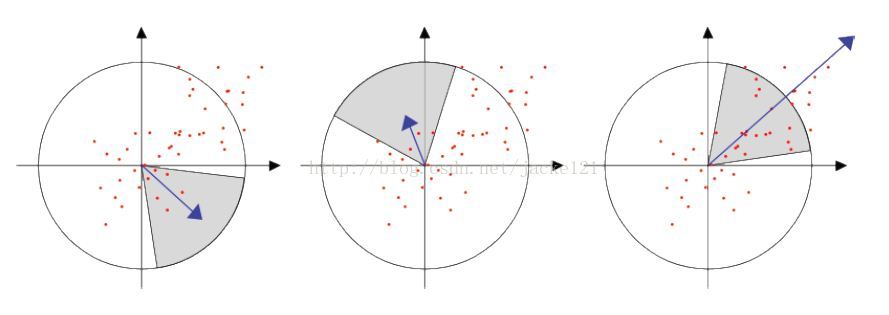
Surf演算法原理:
參考資料:Surf演算法論文及實現原始碼 作為尺度不變特徵變換演算法(Sift演算法)的加速版,Surf演算法在適中的條件下完成兩幅影象中物體的匹配基本實現了實時處理,其快速的基礎實際上只有一個——積分影象haar求導。我們先來看介紹Sift演算法的基本過程,然後再介紹Surf演算法。1、Sift演算法簡介
Sift演算法是David Lowe於1999年提出的區域性特徵描述子,並於2004年進行了更深入的發展和完善。Sift特徵匹配演算法可以處理兩幅影象之間發生平移、旋轉、仿射變換情況下的匹配問題,具有很強的匹配能力。總體來說,Sift運算元具有以下特性: (1) (2)、特徵點過濾並進行精確定位;
(2)、特徵點過濾並進行精確定位;

(3)、為特徵點分配方向值;

(4)、生成特徵描述子。 以特徵點為中心取16*16的鄰域作為取樣視窗,將取樣點與特徵點的相對方向通過高斯加權後歸入包含8個bin的方向直方圖,最後獲得4*4*8的128維特徵描述子。示意圖如下:

當兩幅影象的Sift特徵向量生成以後,下一步就可以採用關鍵點特徵向量的歐式距離來作為兩幅影象中關鍵點的相似性判定度量。取圖1的某個關鍵點,通過遍歷找到影象2中的距離最近的兩個關鍵點。在這兩個關鍵點中,如果次近距離除以最近距離小於某個闕值,則判定為一對匹配點。
2、Surf演算法原理
(1)、構建Hessian矩陣
Hessian矩陣是Surf演算法的核心,為了方便運算,假設函式f(z,y),Hessian矩陣H是由函式,偏導陣列成:
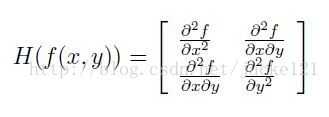
H矩陣判別式為:
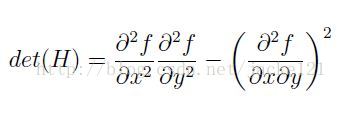
判別式的值是H矩陣的特徵值,可以利用判定結果的符號將所有點分類,根據判別式取值正負,來判別該點是或不是極值點。在SURF演算法中,用影象畫素l(x,y)代替函式值f(x,y),選用二階標準高斯函式作為濾波器,通過特定核間的卷積計算二階偏導數,這樣便能計算出H矩陣的三個矩陣元素L。、L。、k,從而計算出H矩陣:

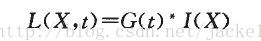
L。(X,£)是一幅影象在不同解析度下的表示,可以利用高斯核G(£)與影象函式,(X)在點X一(z,y)的卷積來實現,核函式G(£)具體表示如式(5),g(£)為高斯函式,t為高斯方差,L。與L。同理。通過這種方法可以為影象中每個畫素計算出其H行列式的決定值,並用這個值來判別特徵點。為方便應用,Herbert Bay提出用近似值現代替L。為平衡準確值與近似值間的誤差引入權值叫,權值硼隨尺度變化,則H矩陣判別式可表示為:

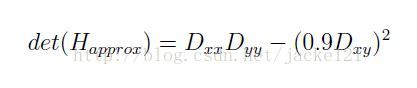
(2)、構建尺度空間 影象的尺度空間是這幅影象在不同解析度下的表示,由式(4)知,一幅影象j(X)在不同解析度下的表示可以利用高斯核G(£)的卷積來實現,影象的尺度大小一般用高斯標準差來表示[6]。在計算視覺領域,尺度空間被象徵性的表述為一個影象金字塔,其中,輸入影象函式反覆與高斯函式的核卷積並反覆對其進行二次抽樣,這種方法主要用於Sift演算法的實現,但每層影象依賴於前一層影象,並且影象需要重設尺寸,因此,這種計算方法運算量較大,而SURF演算法申請增加影象核的尺寸,這也是SIFT演算法與SURF演算法在使用金字塔原理方面的不同。演算法允許尺度空間多層影象同時被處理,不需對影象進行二次抽樣,從而提高演算法效能。圖1(a)是傳統方式建立一個如圖所示的金字塔結構,影象的寸是變化的,並且運(1) 算會反覆使用高斯函式對子層進行平滑處理,圖1(b)說明Surf演算法使原始影象保持不變而只改變濾波器大小。

(3)、精確定位特徵點 所有小於預設極值的取值都被丟棄,增加極值使檢測到的特徵點數量減少,最終只有幾個特徵最強點會被檢測出來。檢測過程中使用與該尺度層影象解析度相對應大小的濾波器進行檢測,以3×3的濾波器為例,該尺度層影象中9個畫素點之一圖2檢測特徵點與自身尺度層中其餘8個點和在其之上及之下的兩個尺度層9個點進行比較,共26個點,圖2中標記‘x’的畫素點的特徵值若大於周圍畫素則可確定該點為該區域的特徵點。

(4)、主方向確定 為保證旋轉不變性[8I,首先以特徵點為中心,計算半徑為6s(S為特徵點所在的尺度值)的鄰域內的點在z、y 方向的Haar小波(Haar小波邊長取4s)響應,並給這些響應值賦高斯權重係數,使得靠近特徵點的響應貢獻大,而遠離特徵點的響應貢獻小,其次將60。範圍內的響應相加以形成新的向量,遍歷整個圓形區域,選擇最長向量的方向為該特徵點的主方向。這樣,通過特徵點逐個進行計算,得到每一個特徵點的主方向。

(5)特徵點描述子生成
首先將座標軸旋轉為關鍵點的方向,以確保旋轉不變性。
接下來以關鍵點為中心取8×8的視窗。圖左部分的中央黑點為當前關鍵點的位置,每個小格代表關鍵點鄰域所在尺度空間的一個畫素,利用公式求得每個畫素的梯度幅值與梯度方向,箭頭方向代表該畫素的梯度方向,箭頭長度代表梯度模值,然後用高斯視窗對其進行加權運算,每個畫素對應一個向量,長度為,為該畫素點的高斯權值,方向為, 圖中藍色的圈代表高斯加權的範圍(越靠近關鍵點的畫素梯度方向資訊貢獻越大)。然後在每4×4的小塊上計算8個方向的梯度方向直方圖,繪製每個梯度方向的累加值,即可形成一個種子點,如圖右部分示。此圖中一個關鍵點由2×2共4個種子點組成,每個種子點有8個方向向量資訊。這種鄰域方向性資訊聯合的思想增強了演算法抗噪聲的能力,同時對於含有定位誤差的特徵匹配也提供了較好的容錯性。