壓縮感知是由E. J. Candes、J. Romberg、T. Tao 和D. L. Donoho於2004年提出來的，但在此前已經出現了雛形，這個不深究。

陶哲軒曾經寫過一篇關於壓縮感知的科普文章《壓縮感知和單畫素相機》，最頂尖的科學獎寫科普文章很難得，當然有必要學習。雖然這篇文章直言是為非數學專業的人寫的，但是理解起來依然非常困難，因為涉及的數學知識非常多，下面我們一起來學習這篇文章，因為本人是初學者，還有很多問題沒搞明白，請多多指教。

1、文章中有這句話：兩百萬個畫素用8位灰度值就是2MB，16位灰度就是4MB。

理解：因為這裡指的是灰度影象，而不是非黑即白的二值影象，所以如果用8位表示的話，在

2、不太高階的壓縮技術引出的問題。

理解：對於給定的一張圖片，我們可以選取可見色塊中色差較小的某塊，記錄該塊的維度、座標和顏色，剩下微小的殘餘誤差。然後繼續搜尋剩餘的色塊，直到整張圖片只剩下色彩強度很小，肉眼無法察覺的細節。反向操作就可以還原出比原始圖片質量低的重建圖片，但是佔用空間卻小很多。

以上演算法不適用於顏色劇烈變化的情況，實際應用不是很有效，因為顏色劇烈變化就沒辦法用平均色塊來表示，而應該用“不均勻色塊”表示：如果右半邊色彩強度平均值大於左半邊這樣的色塊。這種情況可以用二維

JPEG 2000用的就是離散小波變換（DWT），但是比這種“小波係數閾值法”要精細很多。

而一張1024*2048的影象可能會有200百萬自由度，因此需要200多萬個不同的小波來描述，才可能完美重建，而從小波的角度來說，這些小波係數是稀疏的，只有一部分是重要的，另一部分提供極少有用的資訊，可以捨棄掉

可是，我們並不知道哪10萬個是重要的，所以不得不對200多萬個小波係數一一計量，找出重要的10萬個，這就需要200多萬次，非常可怕。如果隨機選取了10萬個係數，但這10萬個係數並不是最重要的，相當於把圖片中有用的資訊丟掉了，這反而弄巧成拙了。

解決辦法：就是用非小波的演算法來做30萬個測量——儘管我前面確實講過小波演算法是觀察和壓縮影象的最佳手段。實際上最好的測量其實應該是（偽）隨機測量——比如說隨機生成30萬個“濾鏡”影象並測量真實影象與每個濾鏡的相關程度。這樣，影象與濾鏡之間的這些測量結果（也就是“相關性”）很有可能是非常小非常隨機的。但是——這是關鍵所在——構成影象的2百萬種可能的小波函式會在這些隨機的濾鏡的測量下生成自己特有的“特徵”，它們每一個都會與某一些濾鏡成正相關，與另一些濾鏡成負相關，但是與更多的濾鏡不相關。可是（在極大的概率下）2百萬個特徵都各不相同；更有甚者，其中任意十萬個的線性組合仍然是各不相同的（以線性代數的觀點來看，這是因為一個30萬維線性子空間中任意兩個10萬維的子空間極有可能互不相交）。因此，基本上是有可能從這30萬個隨機資料中恢復影象的（至少是恢復影象中的10萬個主要細節）。簡而言之，我們是在討論一個雜湊函式的線性代數版本。

意思如下：可以隨機生成30萬個濾鏡影象，應該是指30萬個元素，原圖是200多萬個元素，因為是隨機生成的，所以濾鏡和原圖之間非相關性大，濾鏡和原圖得到的是30萬個隨機資料，這30萬個隨機資料包含了原圖的資訊，而且達到了降維的效果，這其實就是隨機測量矩陣的作用，我們需要做的就是找到一個合適的觀測矩陣，然後從30萬個觀測資料中恢復原始影象。30萬個線性組合不相關表示30萬個方程至少可以解出30萬個未知數，而30萬線性子空間任意兩個10萬維子空間不相交那就說明至少可以解出10萬個未知數，這樣就表示至少可以恢復出影象中的10萬個重要細節。

如果知道200萬個係數中哪10萬個是重要的，就可以利用標準的線性代數來重建影象。事實上我們並不能提前知道哪些係數是重要的，這又如何還原影象呢？可以用最小二乘近似法得出全部200萬個係數，進而得出200萬個畫素重建影象，但還原出的影象會含有大量顆粒噪聲，並不可取。可以為每一組可能的10萬關鍵係數都做一次線性代數處理，但是這樣做的耗時非常恐怖，我認為是C(200萬，10萬)，陶哲軒說大約是10的17萬次方個組合，不可行。

陶哲軒給出了兩種可行的恢復原影象的方法：

NO.1、匹配追蹤法(MP):找到一個其標記看上去與收集到的資料相關的小波；在資料中去除這個標記的所有印跡；不斷重複直到我們能用小波標記“解釋”收集到的所有資料。

看起來並不好懂，那就分步驟解釋吧：

1)從字典矩陣D（過完備原子庫）中選擇一個與原始訊號y最匹配的原子（字典矩陣D中的某列），方法就是：計算訊號 y 與字典矩陣中每列(原子)的內積，選擇絕對值最大的一個原子，它就是與訊號 y 在本次迭代運算中最匹配的原子。

用專業術語說：令訊號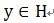，從字典矩陣中選擇一個最為匹配的原子，滿足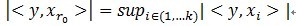，r0 表示一個字典矩陣的列索引。這樣，訊號 y 就被分解為在最匹配原子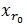的垂直投影分量和殘值兩部分，即：。

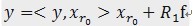2)對殘值R1f按照上面的步驟進行同樣的分解，那麼第K步可以得到：

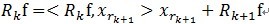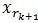， 其中 滿足。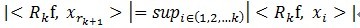

可見，經過K步分解後，訊號 y 被分解為：，其中。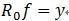

需要說明的是：MP演算法是收斂的，因為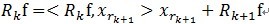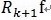，和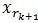正交，由這兩個可以得出，得出每一個殘值比上一次的小，故而收斂。

（上面的公式有些錯誤，我不知道csdn部落格怎麼插入公式，不過大家應該很容易看出來，懂得原理就成了）

NO.2、 基追蹤（又名L1模最小化）：在所有與錄得資料匹配的小波組合中，找到一個“最稀疏的”，也就是其中所有係數的絕對值總和越小越好。（這種最小化的結果趨向於迫使絕大多數係數都消失了。）這種最小化演算法可以利用單純形法之類的凸規劃演算法，在合理的時間內計算出來。

聽起來也不好懂，簡單來說就是：把0範數問題轉化為1範數問題，因為0範數表示的是向量中非零元素的個數，是NP問題，無法求解，可以等價轉化為1範數凸優化問題，1範數的意思就是絕對值之和，因為稀疏，在這裡當然是絕對值總和越小越好。（以後還會具體提到該演算法，下面貼一下甄亮利老師一篇博文的精華部分，便於理解）

這篇文章的權威性是毋庸置疑的，但前面說了理解起來並不簡單，因此本人也有些疑惑的地方。

1、傳統相機會測量每一個畫素的亮度（在上述例子中就是二百萬個測量值），結果得到的圖片檔案就比較大（用8位灰度值就是2MB，16位灰度就是4MB）。數學上就認為這個檔案是用超高維向量值描繪的（在本例中就是約二百萬維）。

疑惑：“超高維向量值”，“約二百萬維”這個是怎麼得來的？應該怎麼計算維度？因為一般說，一張圖無論畫素多少個，我們都認為它是二維的。

2、關鍵是儘管“所有圖片”所構成的空間要佔用2MB的“自由度”或者說“熵”。

疑惑：為什麼說是“自由度”和“熵”？自由度還勉強可以理解，但是說是“熵”我就理解不了了。如果定性不定量理解的話，熵表示的是混亂的程度，某種意義上的自由度。

3、在影象上設定一種合適的“過濾器”或叫“濾鏡”，然後計量過濾出來的每個畫素的色彩強度，是一種可行的係數計量方法。

疑惑：不太懂這個計量方法，這裡說得好像是把色彩強度大的畫素過濾出來。

參考文獻：

1、匹配追蹤演算法基本概念介紹

http://blog.sina.com.cn/s/blog_5156997b0101qu5f.html

2、An introduction to Sparse Representation

http://blog.sciencenet.cn/home.php?mod=space&uid=621576&do=blog&id=551052