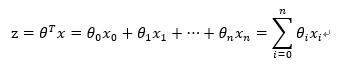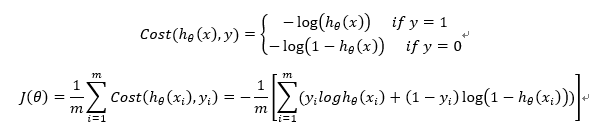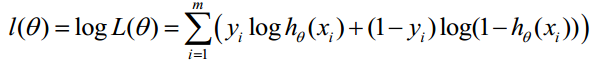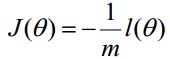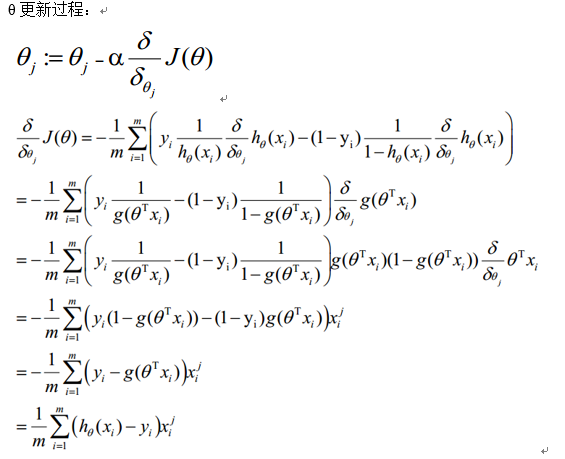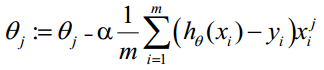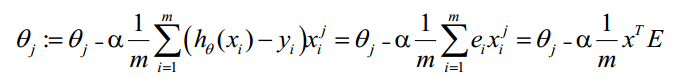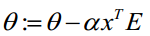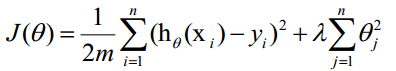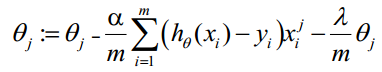邏輯迴歸原理介紹及Matlab實現
一、邏輯迴歸基本概念
1. 什麼是邏輯迴歸
邏輯迴歸就是這樣的一個過程:面對一個迴歸或者分類問題,建立代價函式,然後通過優化方法迭代求解出最優的模型引數,然後測試驗證我們這個求解的模型的好壞。
Logistic迴歸雖然名字裡帶“迴歸”,但是它實際上是一種分類方法,主要用於兩分類問題(即輸出只有兩種,分別代表兩個類別)
迴歸模型中,y是一個定性變數,比如y=0或1,logistic方法主要應用於研究某些事件發生的概率
2. 邏輯迴歸的優缺點
優點:
1)速度快,適合二分類問題
2)簡單易於理解,直接看到各個特徵的權重
3)能容易地更新模型吸收新的資料
缺點:
對資料和場景的適應能力有侷限性,不如決策樹演算法適應性那麼強
3. 邏輯迴歸和多重線性迴歸的區別
Logistic迴歸與多重線性迴歸實際上有很多相同之處,最大的區別就在於它們的因變數不同,其他的基本都差不多。正是因為如此,這兩種迴歸可以歸於同一個家族,即廣義線性模型(generalizedlinear model)。
這一家族中的模型形式基本上都差不多,不同的就是因變數不同。這一家族中的模型形式基本上都差不多,不同的就是因變數不同。
- 如果是連續的,就是多重線性迴歸
- 如果是二項分佈,就是Logistic迴歸
- 如果是Poisson分佈,就是Poisson迴歸
- 如果是負二項分佈,就是負二項迴歸
4. 邏輯迴歸用途
- 尋找危險因素:尋找某一疾病的危險因素等;
- 預測:根據模型,預測在不同的自變數情況下,發生某病或某種情況的概率有多大;
- 判別:實際上跟預測有些類似,也是根據模型,判斷某人屬於某病或屬於某種情況的概率有多大,也就是看一下這個人有多大的可能性是屬於某病。
5. Regression 常規步驟
- 尋找h函式(即預測函式)
- 構造J函式(損失函式)
- 想辦法使得J函式最小並求得迴歸引數(θ)
6. 構造預測函式h(x)
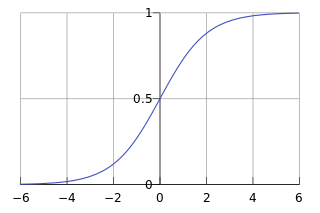
1) Logistic函式(或稱為Sigmoid函式),函式形式為: 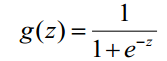
對於線性邊界的情況,邊界形式如下:
其中,訓練資料為向量 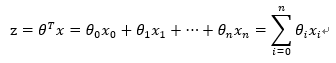
最佳引數
構造預測函式為:
函式h(x)的值有特殊的含義,它表示結果取1的概率,因此對於輸入x分類結果為類別1和類別0的概率分別為:
P(y=1│x;θ)=h_θ (x)
P(y=0│x;θ)=1-h_θ (x)
7.構造損失函式J(m個樣本,每個樣本具有n個特徵)
Cost函式和J函式如下,它們是基於最大似然估計推導得到的。
8. 損失函式詳細推導過程
1) 求代價函式
概率綜合起來寫成: 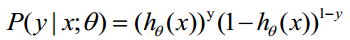
取似然函式為: 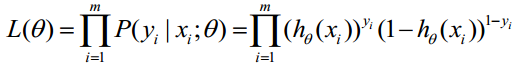
對數似然函式為:
最大似然估計就是求使l(θ)取最大值時的θ,其實這裡可以使用梯度上升法求解,求得的θ就是要求的最佳引數。
在Andrew Ng的課程中將J(θ)取為下式,即:
2) 梯度下降法求解最小值
θ更新過程可以寫成:
9. 向量化
ectorization是使用矩陣計算來代替for迴圈,以簡化計算過程,提高效率。
向量化過程:
約定訓練資料的矩陣形式如下,x的每一行為一條訓練樣本,而每一列為不同的特稱取值:

g(A)的引數A為一列向量,所以實現g函式時要支援列向量作為引數,並返回列向量。
θ更新過程可以改為:
綜上所述,Vectorization後θ更新的步驟如下:
- 求 A=x*θ
- 求 E=g(A)-y
- 求
10.正則化
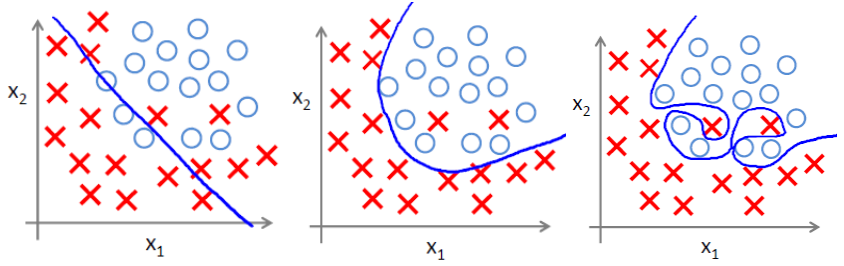
(1) 過擬合問題
過擬合即是過分擬合了訓練資料,使得模型的複雜度提高,繁華能力較差(對未知資料的預測能力)
下面左圖即為欠擬合,中圖為合適的擬合,右圖為過擬合。
(2)過擬合主要原因
過擬合問題往往源自過多的特徵
解決方法
1)減少特徵數量(減少特徵會失去一些資訊,即使特徵選的很好)
• 可用人工選擇要保留的特徵;
• 模型選擇演算法;
2)正則化(特徵較多時比較有效)
• 保留所有特徵,但減少θ的大小
(3)正則化方法
正則化是結構風險最小化策略的實現,是在經驗風險上加一個正則化項或懲罰項。正則化項一般是模型複雜度的單調遞增函式,模型越複雜,正則化項就越大。
正則項可以取不同的形式,在迴歸問題中取平方損失,就是引數的L2範數,也可以取L1範數。取平方損失時,模型的損失函式變為:
lambda是正則項係數:
• 如果它的值很大,說明對模型的複雜度懲罰大,對擬合數據的損失懲罰小,這樣它就不會過分擬合數據,在訓練資料上的偏差較大,在未知資料上的方差較小,但是可能出現欠擬合的現象;
• 如果它的值很小,說明比較注重對訓練資料的擬合,在訓練資料上的偏差會小,但是可能會導致過擬合。
正則化後的梯度下降演算法θ的更新變為:
二、Matlab實現邏輯迴歸
clear
clc
X = xlsread('C:\Users\user01\Desktop\test.xlsx');
[m,n] = size(X);
%資料歸一化處理
X(:,1)=X(:,1)/max(X(:,1));
X(:,2)=X(:,2)/max(X(:,2));
X(:,3)=X(:,3)/max(X(:,3));
X(:,4)=X(:,4)/max(X(:,4));
X(:,5)=X(:,5)/max(X(:,5));
X(:,6)=X(:,6)/max(X(:,6));
%將截距項新增至資料集X
%X=[X,ones(m,1)];
Y=X(:,7);
%我們把資料集中所有序號末位為6的設定為測試集,其他的資料為訓練集
%將資料分為訓練集XX1,YY1,測試集XX2,YY2。
j=1;
k=1;
for i=1:m
if mod(i,10)==9
XX2(j,:)=X(i,:);
YY2(j,:)=Y(i,:);
j=j+1;
else
XX1(k,:)=X(i,:);
YY1(k,:)=Y(i,:);
k=k+1;
end
end
[m1,n1] = size(XX1);
[m2,n2] = size(XX2);
%設定學習率為0.01
delta=0.01;
%收斂到的極值是否與初值無關還待驗證
theta1=rand(6,1);
%訓練模型
%向量化求解theta
%迭代次數num
% num = 100;
% while(num)
% xx = XX1(:,1:4)';
% yy = YY1;
% A = xx' * theta1;
% g = 1/(1+exp(-A));
% E = g' - yy;
% theta2 = theta1 - delta * xx * E;
%
% % temp = theta2-theta1;
% % theta = norm(temp);
% theta1 = theta2;
% num = num - 1;
% end
%%訓練模型
%公式法求解theta
num = 100;
while(num)
dt=zeros(6,1);
for i=1:m1
xx=XX1(i,1:6)';
yy=YY1(i,1);
h=1/(1+exp(-(theta1' * xx)));
dt=dt+(yy-h) * xx;
end
%theta2=theta1+delta*dt;
theta2=theta1 - 1/m1*delta*dt;
%norm(theta2-theta1)
%0.00001
%norm(A) 返回向量A的2範數
temp = theta2-theta1;
theta = norm(temp);
theta1=theta2;
num = num - 1;
end
%測試資料
cc=0;
for i=1:m2
xx=XX2(i,1:6)';
yy=YY2(i);
ans=1/(1+exp(-theta2' * xx));
if ans>0.5 && yy==1
cc=cc+1;
end
if ans<=0.5 && yy==0
cc=cc+1;
end
end
cc/m2
%測試結果: 正確率為 75.73%。