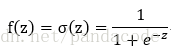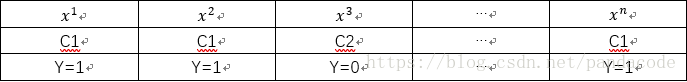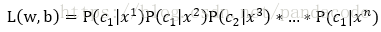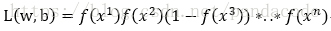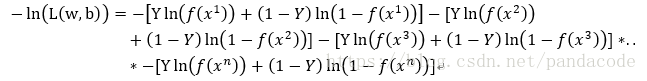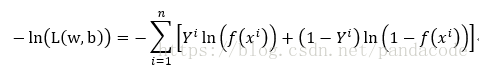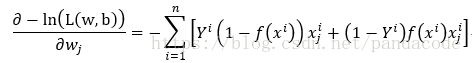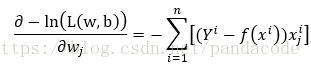邏輯迴歸原理介紹與案例python程式碼實現
阿新 • • 發佈:2019-02-02
邏輯迴歸是用於分類的演算法。
平常的線性迴歸方程為f(x)=wx+b,此時f(x)的取值可以是任意的,要讓預測的值可以分類,例如分類到class1是預測值為1,分類到class2時預測值為0。這時我們就要用到分類函式。
下面來介紹一個分類函式sigmoid:
其中z=wx+b
f(z)的取值將在0與1之間,如下圖
有:
設f(z)表示分類到class1是的概率,則分類到class2的概率為1-f(z)。
假設我們有如下資料集:
最大似然的意義是表示出現這組資料最大可能性。
由最大釋然估計可得
即求L(w,b)最大時的w和b的值
也就是求-ln(L(w,b))最小值時,w和b的值
以下為上述公式的程式碼實現
cross_entropy = -1 * (np.dot(np.squeeze(Y), np.log(y)) + np.dot((1 - np.squeeze(Y)), np.log(1 - y)))
求偏導可得:
以下為上述求偏導的程式碼實現
w_grad = np.sum(-1 * X * (np.squeeze(Y) - y).reshape((batch_size,1)), axis=0)
b_grad = np.sum(-1 * (np.squeeze(Y) - y))可用梯度下降法求得目標函式最低時的w和b的值
以下為邏輯迴歸案例程式碼實現收入分類。
import os, sys import numpy as np from random import shuffle from math import log, floor import pandas as pd #此函式用於載入訓練和測試資料 def load_data(train_data_path, train_label_path, test_data_path): X_train = pd.read_csv(train_data_path, sep=',', header=0) X_train = np.array(X_train.values) Y_train = pd.read_csv(train_label_path, sep=',', header=0) Y_train = np.array(Y_train.values) X_test = pd.read_csv(test_data_path, sep=',', header=0) X_test = np.array(X_test.values) return (X_train, Y_train, X_test) #此函式用於打亂訓練資料的排序 def _shuffle(X, Y): randomize = np.arange(len(X)) np.random.shuffle(randomize) return (X[randomize], Y[randomize]) #此函式用於將訓練和測試資料特徵歸一化 def normalize(X_all, X_test): #將訓練集與測試集合並後歸一化 X_train_test = np.concatenate((X_all, X_test)) mu = (sum(X_train_test) / X_train_test.shape[0]) sigma = np.std(X_train_test, axis=0) mu = np.tile(mu, (X_train_test.shape[0], 1)) sigma = np.tile(sigma, (X_train_test.shape[0], 1)) X_train_test_normed = (X_train_test - mu) / sigma # 歸一化後將資料從新分為訓練集和測試集 X_all = X_train_test_normed[0:X_all.shape[0]] X_test = X_train_test_normed[X_all.shape[0]:] return X_all, X_test #此函式用於將訓練集劃分為要使用的訓練集和用於選擇模型的訓練集 def split_valid_set(X_all, Y_all, percentage): all_data_size = len(X_all) valid_data_size = int(floor(all_data_size * percentage)) X_all, Y_all = _shuffle(X_all, Y_all) X_train, Y_train = X_all[0:valid_data_size], Y_all[0:valid_data_size] X_valid, Y_valid = X_all[valid_data_size:], Y_all[valid_data_size:] return X_train, Y_train, X_valid, Y_valid #定義sigmoid函式 def sigmoid(z): res = 1 / (1.0 + np.exp(-z)) return np.clip(res, 1e-8, 1-(1e-8)) #驗證模型的正確性 def valid(w, b, X_valid, Y_valid): valid_data_size = len(X_valid) z = (np.dot(X_valid, np.transpose(w)) + b) y = sigmoid(z) y_ = np.around(y) result = (np.squeeze(Y_valid) == y_) print('Validation acc = %f' % (float(result.sum()) / valid_data_size)) return def train(X_all, Y_all, save_dir): #劃分0.1的訓練集用於挑選模型 valid_set_percentage = 0.1 X_train, Y_train, X_valid, Y_valid = split_valid_set(X_all, Y_all, valid_set_percentage) # 建立原始引數,設定學習速率、訓練次數、每次訓練用多少資料 w = np.zeros((106,)) b = np.zeros((1,)) l_rate = 0.1 batch_size = 32 train_data_size = len(X_train) step_num = int(floor(train_data_size / batch_size)) epoch_num = 1000 save_param_iter = 50 total_loss = 0.0 #開始訓練 for epoch in range(1, epoch_num): # 模型驗證與儲存引數 if (epoch) % save_param_iter == 0: print('=====Saving Param at epoch %d=====' % epoch) if not os.path.exists(save_dir): os.mkdir(save_dir) np.savetxt(os.path.join(save_dir, 'w'), w) np.savetxt(os.path.join(save_dir, 'b'), [b,]) print('epoch avg loss = %f' % (total_loss / (float(save_param_iter) * train_data_size))) total_loss = 0.0 valid(w, b, X_valid, Y_valid) #將訓練集隨機打亂 X_train, Y_train = _shuffle(X_train, Y_train) # 每batch_size個數據為一組訓練 for idx in range(step_num): X = X_train[idx*batch_size:(idx+1)*batch_size] Y = Y_train[idx*batch_size:(idx+1)*batch_size] z = np.dot(X, np.transpose(w)) + b y = sigmoid(z) cross_entropy = -1 * (np.dot(np.squeeze(Y), np.log(y)) + np.dot((1 - np.squeeze(Y)), np.log(1 - y))) total_loss += cross_entropy w_grad = np.sum(-1 * X * (np.squeeze(Y) - y).reshape((batch_size,1)), axis=0) b_grad = np.sum(-1 * (np.squeeze(Y) - y)) # 梯度下降迭代引數 w = w - l_rate * w_grad b = b - l_rate * b_grad return #輸入測試資料並輸出測試結果 def infer(X_test, save_dir, output_dir): test_data_size = len(X_test) # 載入所得結果引數w和b print('=====Loading Param from %s=====' % save_dir) w = np.loadtxt(os.path.join(save_dir, 'w')) b = np.loadtxt(os.path.join(save_dir, 'b')) # 將w和b與測試集代入函式求得預測值 z = (np.dot(X_test, np.transpose(w)) + b) y = sigmoid(z) y_ = np.around(y) print('=====Write output to %s =====' % output_dir) if not os.path.exists(output_dir): os.mkdir(output_dir) output_path = os.path.join(output_dir, 'log_prediction.csv') with open(output_path, 'w') as f: f.write('id,label\n') for i, v in enumerate(y_): f.write('%d,%d\n' %(i+1, v)) return #主函式 def main(): # Load feature and label X_all, Y_all, X_test = load_data('E:\\kaggle\\income prediction\\X_train', 'E:\\kaggle\\income prediction\\Y_train', 'E:\\kaggle\\income prediction\\X_test') # Normalization X_all, X_test = normalize(X_all, X_test) # To train or to infer train(X_all, Y_all, 'E:\\kaggle\\income prediction') infer(X_test, 'E:\\kaggle\\income prediction', 'E:\\kaggle\\income prediction') return