一、決策樹模型組合

        單決策樹C4.5由於功能太簡單，並且非常容易出現過擬合的現象，於是引申出了許多變種決策樹，就是將單決策樹進行模型組合，形成多決策樹，比較典型的就是迭代決策樹GBRT和隨機森林RF。

        在最近幾年的paper上，如iccv這種重量級會議，iccv 09年的裡面有不少文章都是與Boosting和隨機森林相關的。模型組合+決策樹相關演算法有兩種比較基本的形式：隨機森林RF與GBDT，其他比較新的模型組合+決策樹演算法都是來自這兩種演算法的延伸。

       核心思想：其實很多“漸進梯度”Gradient Boost都只是一個框架，裡面可以套用很多不同的演算法。

        首先說明一下，GBRT這個演算法有很多名字，但都是同一個演算法：

GBRT (Gradient BoostRegression Tree) 漸進梯度迴歸樹

GBDT (Gradient BoostDecision Tree) 漸進梯度決策樹

MART (MultipleAdditive Regression Tree) 多決策迴歸樹

Tree Net決策樹網路

二、GBRT

        迭代決策樹演算法，在阿里內部用得比較多（所以阿里演算法崗位面試時可能會問到），由多棵決策樹組成，所有樹的輸出結果累加起來就是最終答案。它在被提出之初就和SVM一起被認為是泛化能力（generalization)

        GBRT是迴歸樹，不是分類樹。其核心就在於，每一棵樹是從之前所有樹的殘差中來學習的。為了防止過擬合，和Adaboosting一樣，也加入了boosting這一項。

        提起決策樹（DT, DecisionTree）不要只想到C4.5單分類決策樹，GBRT不是分類樹而是迴歸樹！

決策樹分為迴歸樹和分類樹：

        迴歸樹用於預測實數值，如明天溫度、使用者年齡

        分類樹用於分類標籤值，如晴天/陰天/霧/雨、使用者性別

        注意前者結果加減是有意義的，如10歲+5歲-3歲=12歲，後者結果加減無意義

        第一棵樹是正常的，之後所有的樹的決策全是由殘差（此次的值與上次的值之差）來作決策。

三、演算法原理

0.給定一個初始值

1.建立M棵決策樹（迭代M次）

2.對函式估計值F(x)進行Logistic變換

3.對於K各分類進行下面的操作（其實這個for迴圈也可以理解為向量的操作，每個樣本點xi都對應了K種可能的分類yi，所以yi，F(xi)，p(xi)都是一個K維向量）

4.求得殘差減少的梯度方向

5.根據每個樣本點x，與其殘差減少的梯度方向，得到一棵由J個葉子節點組成的決策樹

6.當決策樹建立完成後，通過這個公式，可以得到每個葉子節點的增益（這個增益在預測時候用的）

       每個增益的組成其實也是一個K維向量，表示如果在決策樹預測的過程中，如果某個樣本點掉入了這個葉子節點，則其對應的K個分類的值是多少。比如GBDT得到了三棵決策樹，一個樣本點在預測的時候，也會掉入3個葉子節點上，其增益分別為（假設為3分類問題）：

(0.5, 0.8, 0.1), (0.2, 0.6, 0.3), (0.4, .0.3, 0.3)，那麼這樣最終得到的分類為第二個，因為選擇分類2的決策樹是最多的。

7.將當前得到的決策樹與之前的那些決策樹合併起來，作為一個新的模型（跟6中的例子差不多）

--------------------------------------------------------------------------------------------------------------

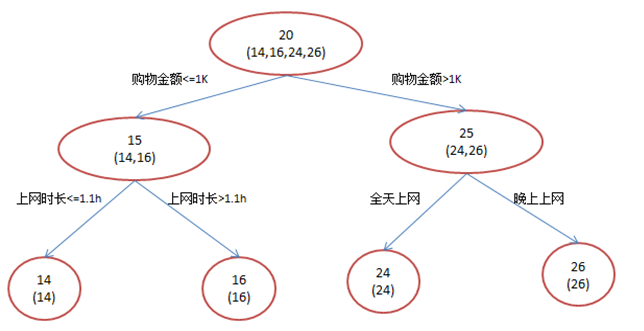
        還是年齡預測，簡單起見訓練集只有4個人，A,B,C,D，他們的年齡分別是14,16,24,26。其中A、B分別是高一和高三學生；C,D分別是應屆畢業生和工作兩年的員工。如果是用一棵傳統的迴歸決策樹來訓練，會得到如下圖1所示結果：

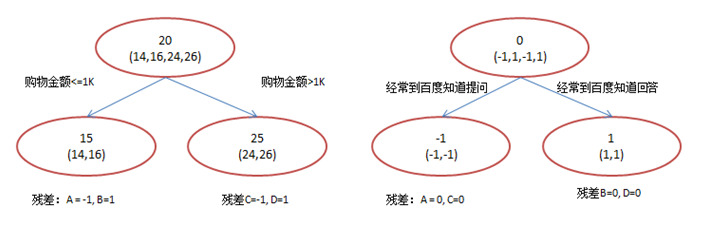
        現在我們使用GBDT來做這件事，由於資料太少，我們限定葉子節點做多有兩個，即每棵樹只有一個分枝，並且限定只學兩棵樹。我們會得到如下圖2所示結果： 

        在第一棵樹分枝和圖1一樣，由於A,B年齡較為相近，C,D年齡較為相近，他們被分為兩撥，每撥用平均年齡作為預測值。此時計算殘差（殘差的意思就是： A的預測值 + A的殘差 = A的實際值），所以A的殘差就是16-15=1（注意，A的預測值是指前面所有樹累加的和，這裡前面只有一棵樹所以直接是15，如果還有樹則需要都累加起來作為A的預測值）。進而得到A,B,C,D的殘差分別為-1,1，-1,1。然後我們拿殘差替代A,B,C,D的原值，到第二棵樹去學習，如果我們的預測值和它們的殘差相等，則只需把第二棵樹的結論累加到第一棵樹上就能得到真實年齡了。這裡的資料顯然是我可以做的，第二棵樹只有兩個值1和-1，直接分成兩個節點。此時所有人的殘差都是0，即每個人都得到了真實的預測值。 

        換句話說，現在A,B,C,D的預測值都和真實年齡一致了。

A: 14歲高一學生，購物較少，經常問學長問題；預測年齡A = 15 – 1 = 14

B: 16歲高三學生；購物較少，經常被學弟問問題；預測年齡B = 15 + 1 = 16

C: 24歲應屆畢業生；購物較多，經常問師兄問題；預測年齡C = 25 – 1 = 24

D: 26歲工作兩年員工；購物較多，經常被師弟問問題；預測年齡D = 25 + 1 = 26  

        那麼哪裡體現了Gradient呢？其實回到第一棵樹結束時想一想，無論此時的cost function是什麼，是均方差還是均差，只要它以誤差作為衡量標準，殘差向量(-1, 1, -1, 1)都是它的全域性最優方向，這就是Gradient。 

四、GBRT適用範圍

        該版本的GBRT幾乎可用於所有的迴歸問題（線性/非線性），相對logistic regression僅能用於線性迴歸，GBRT的適用面非常廣。亦可用於二分類問題（設定閾值，大於閾值為正例，反之為負例）。

五、搜尋引擎排序應用RankNet

        搜尋排序關注各個doc的順序而不是絕對值，所以需要一個新的cost function，而RankNet基本就是在定義這個cost function，它可以相容不同的演算法（GBDT、神經網路...）。

        實際的搜尋排序使用的是Lambda MART演算法，必須指出的是由於這裡要使用排序需要的cost function，LambdaMART迭代用的並不是殘差。Lambda在這裡充當替代殘差的計算方法，它使用了一種類似Gradient*步長模擬殘差的方法。這裡的MART在求解方法上和之前說的殘差略有不同，其區別描述見這裡。

         搜尋排序也需要訓練集，但多數用人工標註實現，即對每個(query, doc)pair給定一個分值（如1, 2, 3, 4），分值越高越相關，越應該排到前面。RankNet就是基於此制定了一個學習誤差衡量方法，即cost function。RankNet對任意兩個文件A,B，通過它們的人工標註分差，用sigmoid函式估計兩者順序和逆序的概率P1。然後同理用機器學習到的分差計算概率P2（sigmoid的好處在於它允許機器學習得到的分值是任意實數值，只要它們的分差和標準分的分差一致，P2就趨近於P1）。這時利用P1和P2求的兩者的交叉熵，該交叉熵就是cost function。

        有了cost function，可以求導求Gradient，Gradient即每個文件得分的一個下降方向組成的N維向量，N為文件個數（應該說是query-doc pair個數）。這裡僅僅是把”求殘差“的邏輯替換為”求梯度“。每個樣本通過Shrinkage累加都會得到一個最終得分，直接按分數從大到小排序就可以了。