【機器學習】演算法原理詳細推導與實現(一):線性迴歸
【機器學習】演算法原理詳細推導與實現(一):線性迴歸
今天我們這裡要講第一個有監督學習演算法,他可以用於一個迴歸任務,這個演算法叫做 線性迴歸
房價預測
假設存在如下 m 組房價資料:
| 面積(m^2) | 價格(萬元) |
|---|---|
| 82.35 | 193 |
| 65.00 | 213 |
| 114.20 | 255 |
| 75.08 | 128 |
| 75.84 | 223 |
| ... | ... |
通過上面的資料,可以做出如下一個圖。橫座標是 面積(m^2),縱座標是 價格(萬元):
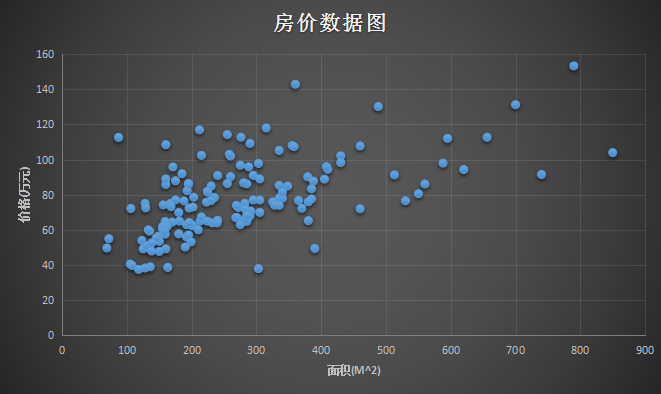
那麼問題來了,給你這樣一組資料,或者給你這樣一個訓練資料的集合,能否預測房屋的面積大小和房價之間的關係?
構建函式
存在如下符號假設:
m 為訓練資料 x 為輸入特徵,即房子的大小 y 為輸出結果,即房子的價格 (x, y) 為一個樣本,即表格中一行代表一個訓練樣本 \((x^{(i)}, y^{(i)})\) 為第 i 個訓練樣本
在監督學習中,我們一般會這樣做:
- 首先找到一個訓練集合
- 提供樣本 m 給演算法構建學習函式
- 演算法會生成一個學習函式,用 \(h(x)\) 表示
- 給學習函式提供足夠的樣本$x$,由此輸出結果$y$
學習函式
graph TD A[訓練集合]--"樣本m"-->B[學習函式] B[學習函式]--"生成"-->C["h(x)"]訓練函式
graph LR A[輸入]--"面積(m^2)"-->B["h(x)"] B["h(x)"]--"價格(萬元)"-->C[輸出]為了設計學習演算法(學習函式),假設存在如下函式:
\[h(x)=\theta_0+\theta_1x \]其中 \(x\) 是一個輸入函式,這裡代表輸入的面積(m^2),\(h(x)\) 是一個輸出函式,這裡代表 輸出的價格(萬元),\(\theta\) 是函式的引數,是需要根據樣本學習的引數。對於如上的學習函式只是一個簡單的二元一次方程,只需要兩組樣本 \((x_0,y_0),(x_1,y_1)\) 就能將 \(\theta_0,\theta_1\) 學習出來,這是一個很簡單的函式,但是這樣在實際情況中並非很合理。
但是影響房子價格的因素不僅僅是房子的大小。除了房子的大小之外,假設這裡還知道每個房子的房間數量:
| 面積(m^2) | 房間(個) | 價格(萬元) |
|---|---|---|
| 82.35 | 2 | 193 |
| 65.00 | 2 | 213 |
| 114.20 | 3 | 255 |
| 75.08 | 2 | 128 |
| 75.84 | 2 | 223 |
| ... | ... | ... |
那麼我們的訓練集合將有第二個特徵,$x_1$表示房子的面積(m^2),$x_2$表示房子的房間(個),這是學習函式就變成了:
\[h(x)=\theta_0+\theta_1x_1+\theta_2x_2=h_\theta(x) \]$\theta$被稱為引數,決定函式中每個特徵$x$的影響力(權重)。\(h_\theta(x)\) 為引數為 \(\theta\) 輸入變數為$x$的學習函式。如果令$x_0=1$,那麼上述方程可以用求和方式寫出,也可以轉化為向量方式表示:
假設存在$m$個特徵$x$,那麼上述公式求和可以改成:
\[\begin{split} h_\theta(x)&=\sum^m_{i=0}{\theta_ix_i} \\ &=\theta^Tx \\ \end{split} \]訓練引數
在擁有足夠多的訓練資料,例如上面的房價資料,怎麼選擇(學習)出引數$\theta$出來?一個合理的方式是使學習函式$h_\theta(x)$ 學習出來的預測值無限接近實際房價值 \(y\)。假設單個樣本誤差表示為:
\[j(\theta)=\frac{1}{2}(h_\theta(x^{(i)})-y^{(i)})^2 \]我們把 \(j(\theta)\) 叫做單個樣本的誤差。至於為什麼前面要乘$\frac{1}{2}$,是為了後面計算方便。
為了表示兩者之間的接近程度,我們可以用訓練資料中所有樣本的誤差的和,所以定義了 損失函式 為:
\[\begin{split} J(\theta)&=j_1(\theta)+j_2(\theta)+...+j_m(\theta) \\ &=\frac{1}{2}\sum^m_{i=1}{(h_\theta(x^{(i)})-y^{(i)})^2} \\ \end{split} \]而最終的目的是為了使誤差和 \(min(J(\theta))\) 最小,這裡會使用一個搜尋演算法來選取 \(\theta\) 使其誤差和無限逼近 \(J(\theta)\) 最小,其流程是:
- 初始化一組向量 \(\vec{\theta}=\vec{0}\)
- 不斷改變 \(\theta\) 的值使其 \(J(\theta)\) 不斷減小
- 直到取得 \(J(\theta)\) 最小值,活得得到最優的引數向量 \(\vec{\theta}\)
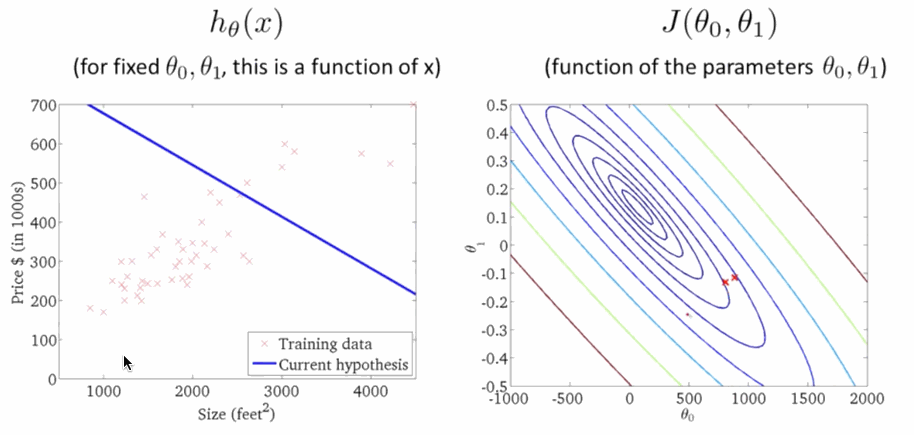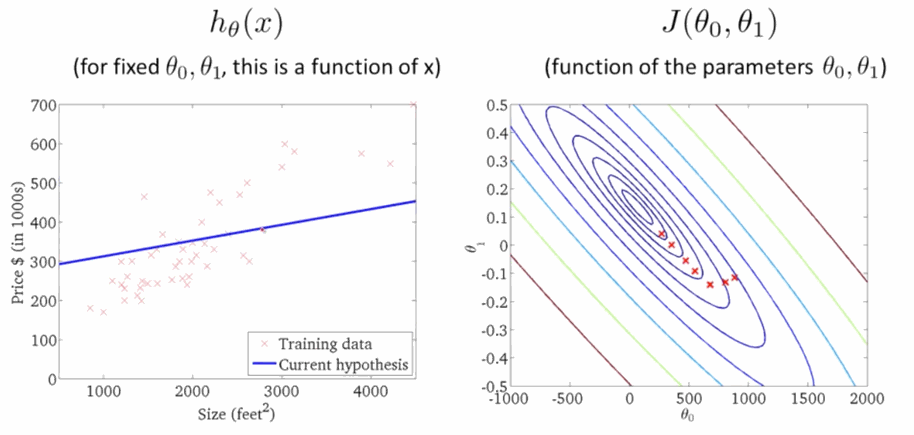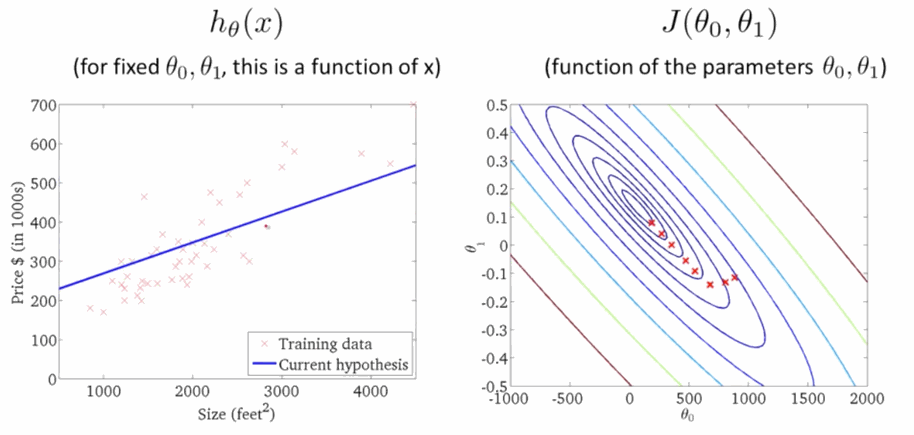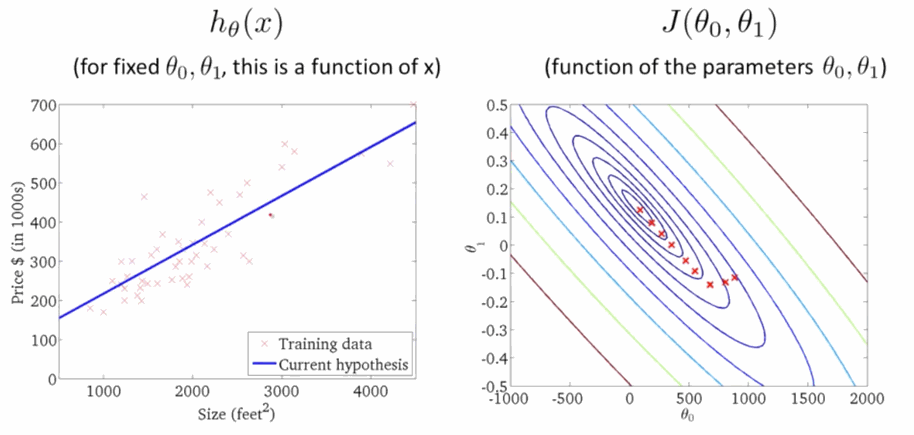
該搜尋演算法為 梯度下降,演算法的思想是這樣的,下圖看到顯示了一個圖形和座標軸,影象的高度表示誤差和 \(J(\theta)\),而下面的兩條座標表示不同的引數 \(\theta\) ,這裡為了方便看圖只是顯示了 \(\theta_0\) 和 \(\theta_1\) ,即變化引數 \(\theta_0\) 和 \(\theta_1\) 使其誤差和 \(J(\theta)\) 在最低點,即最小值。
首先隨機選取一個點 \(\vec{\theta}\) ,它可能是 \(\vec{0}\) ,也可能是隨機的其他向量。最開始的 + 字符號表示開始,搜尋使其 \(J(\theta)\) 下降速度最快的方向,然後邁出一步。到了新的位置後,再次搜尋下降速度最快的方向,然後一步一步搜尋下降,梯度下降演算法是這樣工作的:
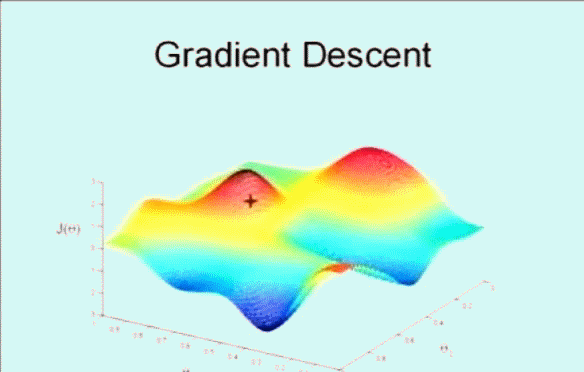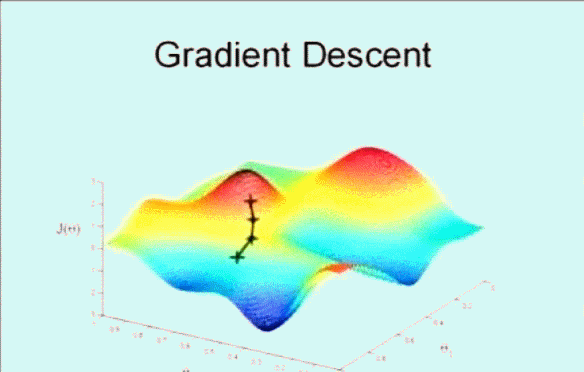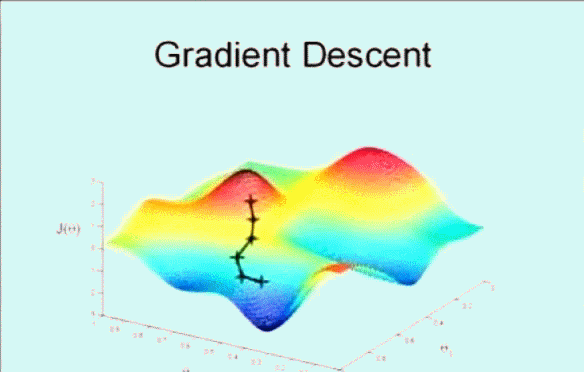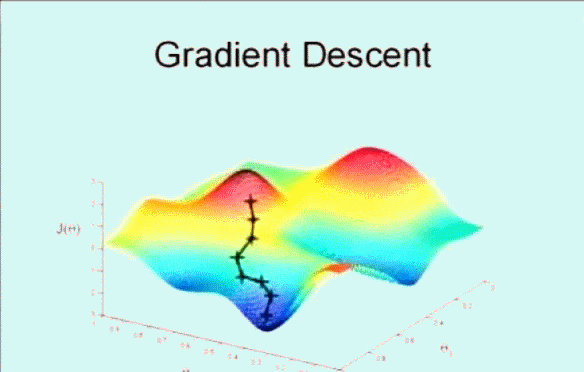
梯度下降的核心就在於每次更新 \(\theta\) 的值,公式為:
\[\theta_j:=\theta_j-\alpha\frac{\partial J(\theta)}{\partial\theta_j}\tag{1} \]上面公式代表:\(\theta_j\) 每次都按照一定的 學習速率 \(\alpha\) 搜尋使誤差和 \(J(\theta)\) 下降最快的方向更新自身的值。而 \(\frac{\partial J(\theta)}{\partial\theta_j}\) 是 \(J(\theta)\) 的偏導值,求偏導得到極值即是下降最快的方向。假設在房價的例子中,只存在一組訓練資料 \((x,y)\),那麼可以推導如下公式:
\[\begin{split} \frac{\partial J(\theta)}{\partial\theta_j}&=\frac{\partial}{\partial\theta_j}\frac{1}{2}(h_{\theta}(x)-y)^2 \\ &=2\frac{1}{2}(h_{\theta}(x)-y)\frac{\partial}{\partial\theta_j}(h_{\theta}(x)-y) \\ &=(h_{\theta}(x)-y)\frac{\partial}{\partial\theta_j}(\sum^m_{i=0}{\theta_ix_i}-y) \\ &=(h_{\theta}(x)-y)\frac{\partial}{\partial\theta_j}(\theta_0x_0+\theta_1x_1+...+\theta_mx_m-y) \\ &=(h_{\theta}(x)-y)x_j \\ \end{split}\tag{2} \]結合 \((1)(2)\) 可以得到:
\[\theta_j:=\theta_j-\alpha(h_{\theta}(x)-y)x_j\tag{3} \]對於存在 \(m\) 個訓練樣本,\((1)\) 轉化為:
\[\theta_j:=\theta_j-\sum^m_{i=1}\alpha(h_{\theta}(x^{(i)})-y^{(i)})x_j\tag{4} \]學習速率 \(\alpha\) 是梯度下降的速率,\(\alpha\) 越大函式收斂得越快,\(J(\theta)\) 可能會遠離最小值,精度越差;\(\alpha\) 越小函式收斂得越慢,\(J(\theta)\) 可能會靠近最小值,精度越高。下面就是下降尋找最小值的過程,在右圖 \(J(\theta)\) 越來越小的時候,左邊的線性迴歸越來準:
程式碼
選取得到的 150條二手房 資料進行預測和訓練,擬合情況如下:

計算損失函式:
# 損失函式
def computeCost(X, y, theta):
inner = np.power(((X * theta.T) - y), 2)
return np.sum(inner) / (2 * len(X))
梯度下降函式為:
# 梯度下降函式
def gradientDescent(X, y, theta, alpha, iters):
temp = np.matrix(np.zeros(theta.shape))
parameters = int(theta.ravel().shape[1])
cost = np.zeros(iters)
for i in range(iters):
error = (X * theta.T) - y
for j in range(parameters):
term = np.multiply(error, X[:, j])
temp[0, j] = theta[0, j] - ((alpha / len(X)) * np.sum(term))
theta = temp
cost[i] = computeCost(X, y, theta)
return theta, cost
訓練迭代1000次後得到引數 \(\theta\):
# 訓練函式
def train_function():
X, y, theta = get_training_dataset()
# 有多少個x就生成多少個theta
theta = np.matrix(np.zeros(X.shape[-1]))
# 檢視初始誤差
# first_cost=computeCost(X, y, theta)
# print(first_cost)
# 設定引數和步長
alpha = 0.01
iters = 1000
# 訓練得到theta和每一次訓練的誤差
g, cost = gradientDescent(X, y, theta, alpha, iters)
computeCost(X, y, g)
return g, cost
資料和程式碼下載請關注公眾號【 TTyb 】,後臺回覆【 機器學習 】即可獲取:

相關推薦
【機器學習】演算法原理詳細推導與實現(一):線性迴歸
【機器學習】演算法原理詳細推導與實現(一):線性迴歸 今天我們這裡要講第一個有監督學習演算法,他可以用於一個迴歸任務,這個演算法叫做 線性迴歸 房價預測 假設存在如下 m 組房價資料: 面積(m^2) 價格(萬元) 82.35 193 65.00 213 114.20 255 75.
【機器學習】演算法原理詳細推導與實現(二):邏輯迴歸
【機器學習】演算法原理詳細推導與實現(二):邏輯迴歸 在上一篇演算法中,線性迴歸實際上是 連續型 的結果,即 \(y\in R\) ,而邏輯迴歸的 \(y\) 是離散型,只能取兩個值 \(y\in \{0,1\}\),這可以用來處理一些分類的問題。 logistic函式 我們可能會遇到一些分類問題,例如想要劃
【機器學習】演算法原理詳細推導與實現(三):樸素貝葉斯
【機器學習】演算法原理詳細推導與實現(三):樸素貝葉斯 在上一篇演算法中,邏輯迴歸作為一種二分類的分類器,一般的迴歸模型也是是判別模型,也就根據特徵值來求結果概率。形式化表示為 \(p(y|x;\theta)\),在引數 \(\theta\) 確定的情況下,求解條件概率 \(p(y|x)\) 。通俗的解釋為:
【機器學習】演算法原理詳細推導與實現(四):支援向量機(上)
【機器學習】演算法原理詳細推導與實現(四):支援向量機(上) 在之前的文章中,包括線性迴歸和邏輯迴歸,都是以線性分界線進行分割劃分種類的。而本次介紹一種很強的分類器【支援向量機】,它適用於線性和非線性分界線的分類方法。 函式間隔概念 為了更好的理解非線性分界線,區別兩種分界線對於分類的直觀理解,第一種直觀理解
【機器學習】演算法原理詳細推導與實現(五):支援向量機(下)
【機器學習】演算法原理詳細推導與實現(五):支援向量機(下) 上一章節介紹了支援向量機的生成和求解方式,能夠根據訓練集依次得出\(\omega\)、\(b\)的計算方式,但是如何求解需要用到核函式,將在這一章詳細推導實現。 核函式 在講核函式之前,要對上一章節得到的結果列舉出來。之前需要優化的凸函式為: \[
【機器學習】演算法原理詳細推導與實現(六):k-means演算法
【機器學習】演算法原理詳細推導與實現(六):k-means演算法 之前幾個章節都是介紹有監督學習,這個章節介紹無監督學習,這是一個被稱為k-means的聚類演算法,也叫做k均值聚類演算法。 聚類演算法 在講監督學習的時候,通常會畫這樣一張圖: 這時候需要用logistic迴歸或者SVM將這些資料分成正負兩
【機器學習】演算法原理詳細推導與實現(七):決策樹演算法
# 【機器學習】演算法原理詳細推導與實現(七):決策樹演算法 在之前的文章中,對於介紹的分類演算法有[邏輯迴歸演算法](https://www.cnblogs.com/TTyb/p/10976291.html)和[樸素貝葉斯演算法](https://www.cnblogs.com/TTyb/p/109890
【機器學習】XgBoost 原理詳解 數學推導
XgBoost (Xtreme Gradient Boosting 極限 梯度 增強) 1.基本描述: 假設Xg-模型有 t 顆決策樹數,t棵樹有序串聯構成整個模型,各決策樹的葉子節點數為 k1,k2,...,kt,
【機器學習】AdaBoost 原理詳解 數學推導
AdaBoost 自適應 增強 Boosting系列代表演算法,對同一訓練集訓練出不同的(弱)分類器,然後集合這些弱分類器構成一個更優效能的(強)分類器
【機器學習】演算法模型效能中的偏差、方差概念
什麼時候模型的複雜程度該停止? 模型越複雜,單次預測出的結果與真實結果的偏差(bias)就越小。但很容易引發過擬合。 模型越簡單,預測不同資料,預測的準確性差別越小。預測不同資料,所得到的準確性構成序列,序列的方差(variance)也就越小。
【機器學習】演算法面試知識點整理(持續更新中~)
1、監督學習(SupervisedLearning):有類別標籤的學習,基於訓練樣本的輸入、輸出訓練得到最優模型,再使用該模型預測新輸入的輸出;代表演算法:決策樹、樸素貝葉斯、邏輯迴歸、KNN、SVM、
【機器學習】谷歌的速成課程(一)
label spa dev 分類 ram 做出 org ron 表示 問題構建 (Framing) 什麽是(監督式)機器學習?簡單來說,它的定義如下: 機器學習系統通過學習如何組合輸入信息來對從未見過的數據做出有用的預測。 標簽 在簡單線性回歸中,標簽是我們要預測
【機器學習】CART分類決策樹+程式碼實現
1. 基礎知識 CART作為二叉決策樹,既可以分類,也可以迴歸。 分類時:基尼指數最小化。 迴歸時:平方誤差最小化。 資料型別:標值型,連續型。連續型分類時採取“二分法”, 取中間值進行左右子樹的劃分。 2. CART分類樹 特徵A有N個取值,將每個取值作為分界點,將資料
【機器學習】迭代決策樹GBRT(漸進梯度迴歸樹)
一、決策樹模型組合 單決策樹C4.5由於功能太簡單,並且非常容易出現過擬合的現象,於是引申出了許多變種決策樹,就是將單決策樹進行模型組合,形成多決策樹,比較典型的就是迭代決策樹GBRT和隨機森林RF。 在最近幾年的paper上,如iccv這種重量級會議,iccv 09年的裡面有不少
【機器學習】EM演算法詳細推導和講解
眾所周知,極大似然估計是一種應用很廣泛的引數估計方法。例如我手頭有一些東北人的身高的資料,又知道身高的概率模型是高斯分佈,那麼利用極大化似然函式的方法可以估計出高斯分佈的兩個引數,均值和方差。這個方法基本上所有概率課本上都會講,我這就不多說了,不清楚的請百度。 然而現在我面臨的是這種情況,我
【轉載】【機器學習】EM演算法詳細推導和講解
今天不太想學習,炒個冷飯,講講機器學習十大演算法裡有名的EM演算法,文章裡面有些個人理解,如有錯漏,還請讀者不吝賜教。 眾所周知,極大似然估計是一種應用很廣泛的引數估計方法。例如我手頭有一些東北人的身高的資料,又知道身高的概率模型是高斯分佈,那麼利用極大化似然函式的
【機器學習】Apriori演算法——原理及程式碼實現(Python版)
Apriopri演算法 Apriori演算法在資料探勘中應用較為廣泛,常用來挖掘屬性與結果之間的相關程度。對於這種尋找資料內部關聯關係的做法,我們稱之為:關聯分析或者關聯規則學習。而Apriori演算法就是其中非常著名的演算法之一。關聯分析,主要是通過演算法在大規模資料集中尋找頻繁項集和關聯規則。
【機器學習】【層次聚類演算法-1】HCA(Hierarchical Clustering Alg)的原理講解 + 示例展示數學求解過程
層次聚類(Hierarchical Clustering)是聚類演算法的一種,通過計算不同類別資料點間的相似度來建立一棵有層次的巢狀聚類樹。在聚類樹中,不同類別的原始資料點是樹的最低層,樹的頂層是一個聚類的根節點。建立聚類樹有自下而上合併和自上而下分裂兩種方法,本篇文章介紹合併方法。層次聚類的合併演算法層次聚
【機器學習】決策樹(上)——從原理到演算法實現
前言:決策樹(Decision Tree)是一種基本的分類與迴歸方法,本文主要討論分類決策樹。決策樹模型呈樹形結構,在分類問題中,表示基於特徵對例項進行分類的過程。它可以認為是if-then規則的集合,也可以認為是定義在特徵空間與類空間上的條件概率分佈。相比樸素
【機器學習】支援向量機SVM原理及推導
參考:http://blog.csdn.net/ajianyingxiaoqinghan/article/details/72897399 部分圖片來自於上面部落格。 0 由來 在二分類問題中,我們可以計算資料代入模型後得到的結果,如果這個結果有明顯的區別,
