博弈(alpha-beta 剪枝)POJ —— 1085 Triangle War
阿新 • • 發佈:2019-01-31
Triangle War
Two players, A and B, take turns filling in any dotted line connecting two dots, with A starting first. Once a line is filled, it cannot be filled again. If the line filled by a player completes one or more triangles, she owns the completed triangles and she is awarded another turn (i.e. the opponent skips a turn). The game ends after all dotted lines are filled in, and the player with the most triangles wins the game. The difference in the number of triangles owned by the two players is not important.
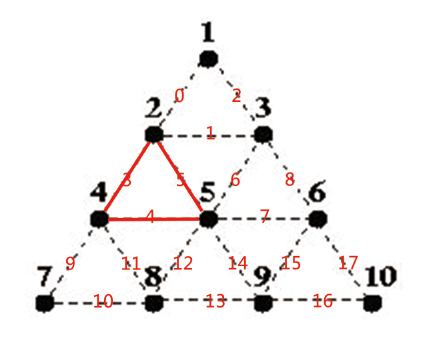
For example, if A fills in the line between 2 and 5 in the partial game on the left below:
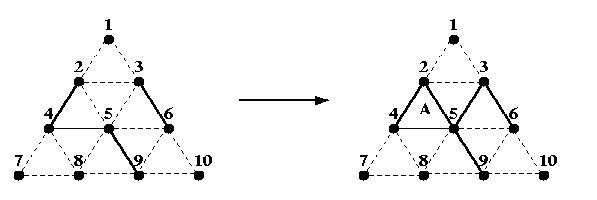
Then, she owns the triangle labelled A and takes another turn to fill in the line between 3 and 5. B can now own 3 triangles (if he wishes) by filling in the line between 2 and 3, then the one between 5 and 6, and finally the one between 6 and 9. B would then make one more move before it is A's turn again.
In this problem, you are given a number of moves that have already been made. From the partial game, you should determine which player will win assuming that each player plays a perfect game from that point on. That is, assume that each player always chooses the play that leads to the best possible outcome for himself/herself.
| Time Limit: 1000MS | Memory Limit: 65536K |
| Total Submissions: 3066 | Accepted: 1207 |
Description
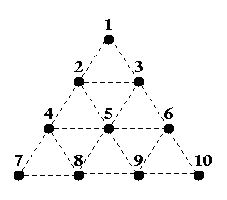
Triangle War is a two-player game played on the following triangular grid:
Two players, A and B, take turns filling in any dotted line connecting two dots, with A starting first. Once a line is filled, it cannot be filled again. If the line filled by a player completes one or more triangles, she owns the completed triangles and she is awarded another turn (i.e. the opponent skips a turn). The game ends after all dotted lines are filled in, and the player with the most triangles wins the game. The difference in the number of triangles owned by the two players is not important.
For example, if A fills in the line between 2 and 5 in the partial game on the left below:

Then, she owns the triangle labelled A and takes another turn to fill in the line between 3 and 5. B can now own 3 triangles (if he wishes) by filling in the line between 2 and 3, then the one between 5 and 6, and finally the one between 6 and 9. B would then make one more move before it is A's turn again.
In this problem, you are given a number of moves that have already been made. From the partial game, you should determine which player will win assuming that each player plays a perfect game from that point on. That is, assume that each player always chooses the play that leads to the best possible outcome for himself/herself.
Input
Output
Sample Input
4 6 2 4 4 5 5 9 3 6 2 5 3 5 7 2 4 4 5 5 9 3 6 2 5 3 5 7 8 6 1 2 2 3 1 3 2 4 2 5 4 5 10 1 2 2 5 3 6 5 8 4 7 6 10 2 4 4 5 4 8 7 8
Sample Output
Game 1: B wins. Game 2: A wins. Game 3: A wins. Game 4: B wins.
題意:
遊戲有A、B兩人蔘與。A先走,每人每次任選一條虛線填成實線。而如果某人填完一條線段後,該線段與另外兩條相鄰的實線組成了一個單位三角形,該三角形被標記為該遊戲者所有,且該遊戲者必須接著再填一條虛線。當18條線段被填充完畢後,擁有三角形多的玩家獲勝。
首先輸入一個數 T ,表示試驗次數;接著一個數 n,表示當前局面已經走了 n 條邊;接著輸入 n 對數,每對數字表示一條填充邊,由 A 開始。問從給出的局面開始,雙方都採取最優策略,最終誰會取勝。
思路:
顯然是博弈問題,也是 alpha-beta 搜尋演算法的基礎應用(博弈基礎:點選開啟連結)。一個比較關鍵的問題是局面的儲存。整個棋盤有18條邊,因此可以用一個整型來儲存一個局面,具體就是:
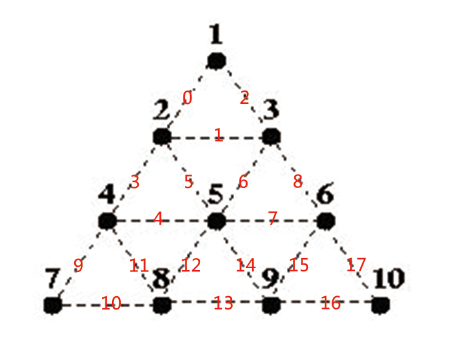
如果每條邊用紅色數字表示(當然也可以不這樣排列),則用 2^0 = 1 表示 edge(1, 2) 或 edge(2, 1),用 2^1 = 2(即二進位制10)表示 edge(2, 3) 或 edge(3, 2),用2^2 = 4(即二進位制100)表示 edge(1, 3) 或 edge(3, 1) ...
那這個局面用哪個數儲存?用 2^3 + 2^4 + 2^5 = 56 表示;其餘單位三角形可用同樣的方法計算。
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
// 儲存每條邊代表的數字
int edge[11][11]={
{0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0},
{0, 0, 0, 2, 0, 0, 0, 0, 0, 0, 0},
{0, 0, 0, 1, 3, 5, 0, 0, 0, 0, 0},
{0, 2, 1, 0, 0, 6, 8, 0, 0, 0, 0},
{0, 0, 3, 0, 0, 4, 0, 9, 11,0, 0},
{0, 0, 5, 6, 4, 0, 7, 0, 12,14,0},
{0, 0, 0, 8, 0, 7, 0, 0, 0, 15,17},
{0, 0, 0, 0, 9, 0, 0, 0, 10,0, 0},
{0, 0, 0, 0, 11,12,0, 10,0, 13, 0},
{0, 0, 0, 0, 0, 14,15,0, 13, 0, 16},
{0, 0, 0, 0, 0, 0, 17,0, 0, 16,0},
};
// 儲存每個單位三角形代表的數字
int tri[9] = {7, 56, 98, 448, 3584, 6160, 28672, 49280, 229376};
int end_state = (1<<18)-1; // 終結狀態 2^18 - 1 ,即所有邊均被填充
int inf = (1<<20);
int next_state(int cur_state, int edge, int *cnt)
{
int i;
int new_state = (cur_state | edge); // 當前局面並上一條邊形成新局面
for(i = 0; i < 9; i++) // 如果新局面能形成一個新的單位三角形,則 cnt++
if(((cur_state & tri[i]) != tri[i]) && ((new_state & tri[i]) == tri[i]))
(*cnt)++;
return new_state;
}
int alpha_beta(int player, int cur_state, int alpha, int beta, int ca, int cb)
{
int remain;
// 如 A 得到 5 分以上則 A 贏
// 如 B 得到 5 分以上則 A 輸
if(ca >= 5) return 1;
if(cb >= 5) return -1;
remain = ((~cur_state) & end_state); // 計算剩餘可走的邊
if(player){ // A 走
while(remain){ // 有可走邊
int move = (remain & (-remain)); // 選擇一條可走邊
int ta = ca;
int val;
// A 填了邊後形成新的局面
int new_state = next_state(cur_state, move, &ta);
if(ta > ca) // 如果 A 得分了,則 A 繼續填一條邊
val = alpha_beta(player, new_state, alpha, beta, ta, cb);
else // 否則輪到 B 填
val = alpha_beta(player^1, new_state, alpha, beta, ca, cb);
if(val > alpha)
alpha = val;
if(alpha >= beta)
return alpha;
remain -= move; // 把邊 move 從剩餘可選邊 remain 中移除
}
return alpha;
}
else{ // B 走
while(remain){
int move = (remain & (-remain));
int tb = cb;
int val;
int new_state = next_state(cur_state, move, &tb);
if(tb > cb)
val = alpha_beta(player, new_state, alpha, beta, ca, tb);
else
val = alpha_beta(player^1, new_state, alpha, beta, ca, cb);
if(val < beta)
beta = val;
if(alpha >= beta)
return beta;
remain -= move;
}
return beta;
}
}
int main()
{
#if 0
freopen("in.txt","r",stdin);
#endif
int T, w = 0;
scanf("%d", &T);
while(T--){
int i;
int n;
int ans;
int cnt = 0; // 偶數輪到 A 走,奇數輪到 B 走
int cur_state = 0; // 當前局面
int ca = 0; // A 的得分
int cb = 0; // B 的得分
int ta, tb;
int alpha = -inf;
int beta = inf;
scanf("%d", &n);
for(i = 0; i < n; i++){
int u, v;
ta = ca;
tb = cb;
scanf("%d%d", &u, &v);
cur_state = next_state(cur_state, 1<<edge[u][v], (cnt & 1) ? (&cb) : (&ca));
if(ta == ca && tb == cb) // 不得分,輪到對方走
cnt++;
}
if(cnt & 1)
ans = alpha_beta(0, cur_state, alpha, beta, ca, cb);
else
ans = alpha_beta(1, cur_state, alpha, beta, ca, cb);
if(ans > 0)
printf("Game %d: A wins.\n", ++w);
else
printf("Game %d: B wins.\n", ++w);
}
return 0;
}