Alpha-Beta剪枝
用於裁剪搜尋樹中沒有意義的不需要搜尋的樹枝，以提高運算速度。
假設α為下界，β為上界，對於α ≤ N ≤ β:
若 α ≤ β 則N有解。
若 α > β 則N無解。
下面通過一個例子說明Alpha-Beta剪枝演算法

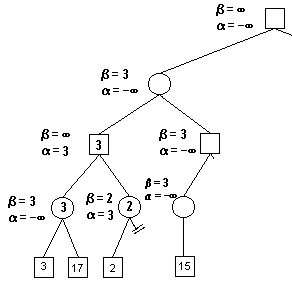
上圖為整顆搜尋樹。這裡使用極小極大演算法配合Alpha-Beta剪枝演算法，正方形為自己（A），圓為對手（B）。
初始設定α為負無窮大，β為正無窮大。

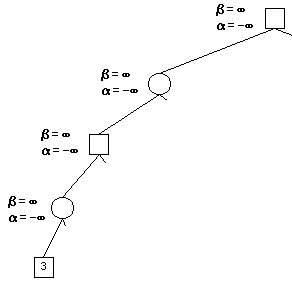
對於B(第四層)而已，儘量使得A獲利最小，因此當遇到使得A獲利更小的情況，則需要修改β。這裡3小於正無窮大，所以β修改為3。

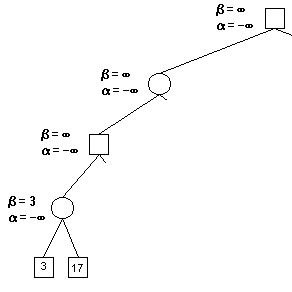
(第四層)這裡17大於3，不用修改β。

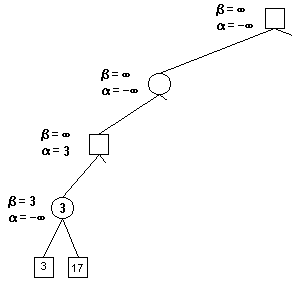
對於A(第三層)而言，自己獲利越大越好，因此遇到利益值大於α時候，需要α進行修改，這裡3大於負無窮大，所以α修改為3

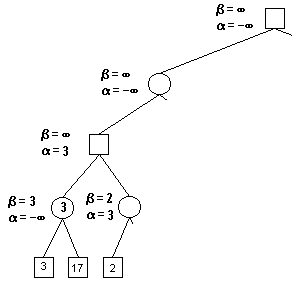
B(第四層)擁有一個方案使得A獲利只有2，α=3, β=2, α > β, 說明A(第三層)只要選擇第二個方案, 則B必然可以使得A的獲利少於A(第三層)的第一個方案,這樣就不再需要考慮B(第四層)的其他候選方案了,因為A(第三層)根本不會選取第二個方案,多考慮也是浪費.

B(第二層)要使得A利益最小,則B(第二層)的第二個方案不能使得A的獲利大於β, 也就是3. 但是若B(第二層)選擇第二個方案, A(第三層)可以選擇第一個方案使得A獲利為15, α=15, β=3, α > β, 故不需要再考慮A(第三層)的第二個方案, 因為B(第二層)不會選擇第二個方案.

A(第一層)使自己利益最大,也就是A(第一層)的第二個方案不能差於第一個方案, 但是A(第三層)的一個方案會導致利益為2, 小於3, 所以A(第三層)不會選擇第一個方案, 因此B(第四層)也不用考慮第二個方案.

當A(第三層)考慮第二個方案時,發現獲得利益為3,和A(第一層)使用第一個方案利益一樣.如果根據上面的分析A(第一層)優先選擇了第一個方案,那麼B不再需要考慮第二種方案,如果A(第一層)還想進一步評估兩個方案的優劣的話, B(第二層)則還需要考慮第二個方案,若B(第二層)的第二個方案使得A獲利小於3,則A(第一層)只能選擇第一個方案,若B(第二層)的第二個方案使得A獲利大於3,則A(第一層)還需要根據其他因素來考慮最終選取哪種方案.