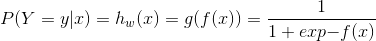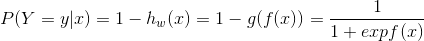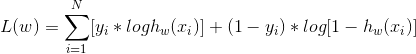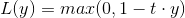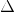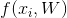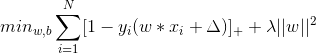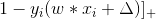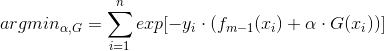機器學習-損失函式彙總
在統計學習中,當有了模型的假設空間,則需要考慮通過什麼樣的準則學習或選擇最優的模型,然而需要引入損失函式與風險函式的概念。
損失函式是度量模型一次預測的好壞;
風險函式是度量平均意義下模型預測的好壞;
0-1損失函式:
使用0-1損失函式時,實質就是通過比較預測值與真實值的符合是否相同;
log對數損失函式(logistic迴歸)
log損失函式的標準形式:
在logistic迴歸中,首先假設樣本服從伯路利分佈(0-1),然後求取該分佈的極大似然估計,在求取極大似然估計的時候對函式進行取對數。
利用已知的樣本分佈,找到最優可能導致這種分佈的引數值w;
上文中提到的
又因為log函式是單調遞增的函式,所以log P(Y|X)同樣會取到最大值,然而加負號,意味著可以取到最小值;
在logistic分佈中;X的分佈函式和密度函式為:
然而,邏輯迴歸的P(Y=y|x)的表示式為:
當y=1時:
當y=0時,
似然函式表示式為:
對數似然損失函式表示式為:
再強調一下,因為log 是單調遞增函式,說以這個式子可以求取L(w)的極大值,得到w的估計值;
接下來是,邏輯迴歸最後得到的目標式子如下:
Hinge損失函式(SVM)
Hinge損失函式的標準形式為:(二分類的情況)
y 為預測值(-1,1)之間, t為目標值+1,-1
SVM的損失函式目的:使SVM分類器在正確分類上的得分始終比不正確分類上的得分高出一個邊界值
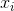

類別的分值計算公式:
然而第 j 個類別的估測得分將表示為:
損失函式定義為:

當
在SVM中,最優化問題則轉化為下列式子:
而目標函式中的第一項是經驗損失,正為上文中講到的Hinge 損失函式;
第一項的取值,取決於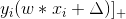
反之,則損失為
第二項是係數為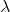
指數損失函式(Adaboost)
在Adaboost演算法中,該演算法是一個前向分步加法演算法的特例,是一個加和模型,損失函式為指數函式
指數損失函式的標準形式為:
當給定n個樣本時的損失函式為:
接下來,我們學習Adaboost演算法中的損失函式,當Adaboost經過 m 次迭代後,得到的函式為:
其中,

由此帶入上式可得:
實質上每次迭代的目的就是尋找引數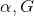
平方損失函式(最小二乘法)
平方損失函式的標準形式為:
當樣本個數為 n 時,損失函式則為:
真實值與估測值之間的差距,我們就是要力求差距最小化