目錄

常用的啟用函式

我們常用的啟用函式有sigmoid，tanh，ReLU這三個函式，我們都來學習學習吧。

sigmoid函式

在深度學習中，我們經常會使用到sigmoid函式作為我們的啟用函式，特別是在二分類上，sigmoid函式是比較好的一個選擇，以下就是sigmoid函式的公式：

sigmoid(x)=11+e−x(1)$$\begin{array}{}\text{(1)}& sigmoid(x)=\frac{1}{1+e^{-x}}\end{array}$$
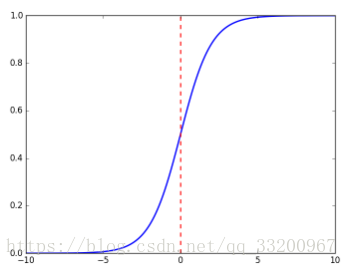
sigmoid函式的座標圖是：

sigmoid函式的程式碼實現：

import numpy as np

def sigmoid(x):
    s = 1 / (1 + np.exp(-x))
    return
 
 s

因為是使用numpy實現的sigmoid函式的，所以這個sigmoid函式可以計算實數、向量和矩陣，如下面的就是當x是實數的時候：

if __name__ == '__main__':
    x = 3
    s = sigmoid(x)
    print s

然後會輸出：

0.952574126822

當x是向量或者矩陣是，計算公式如下：

sigmoid(x)=sigmoid⎛⎝⎜⎜⎜x1x2...xn⎞⎠⎟⎟⎟=⎛⎝⎜⎜⎜⎜⎜11+e−x111+e−x2...11+e−xn⎞⎠⎟⎟⎟⎟⎟(2)$$\begin{array}{}\text{(2)}& sigmoid(x)=sigmoid\left(\begin{array}{c}{x}_1\\ x_2\\ ...\\ x_n\end{array}\right)=(\end{array}$$

11+e−x111+e−x2...11+e−xn)
使用sigmoid函式如下：

if __name__ == '__main__':
    x = np.array([2, 3, 4])
    s = sigmoid(x)
    print s

輸出的結果是：

[0.88079708 0.95257413 0.98201379]

sigmoid函式的梯度

為什麼要計算sigmoid函式的梯度，比如當我們在使用反向傳播來計算梯度，以優化損失函式。當使用的啟用函式是sigmoid函式就要計算sigmoid函式的梯度了。計算公式如下：

sigmoid_derivative(x)

=σ′(x)=σ(x)(1−σ(x))(3)$$\begin{array}{}\text{(3)}& sigmoid\mathrm{\_}derivative(x)={\sigma }^{\prime }(x)=\sigma (x)(1-\sigma (x))\end{array}$$
Python你程式碼實現：

import numpy as np

def sigmoid_derivative(x):
    s = 1 / (1 + np.exp(-x))
    ds = s * (1 - s)
    return ds

當x是實數時，計算如下：

if __name__ == '__main__':
    x = 3
    s = sigmoid_derivative(x)
    print s

輸出結果如下：

0.0451766597309

當x是矩陣或者向量時，計算如下：

if __name__ == '__main__':
    x = np.array([2, 3, 4])
    s = sigmoid_derivative(x)
    print s

輸出結果如下：

[0.10499359 0.04517666 0.01766271]

tanh函式

tanh也是一個常用的啟用函式，它的公式如下：

tanh(x)=ex−e−xex+e−x(4)$$\begin{array}{}\text{(4)}& tanh(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}\end{array}$$
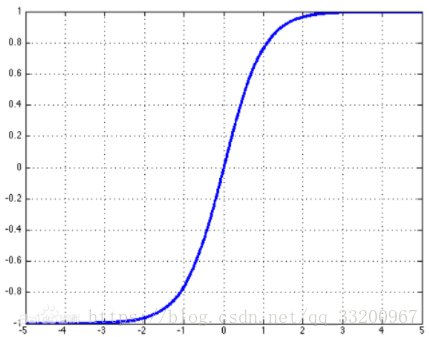
tanh的座標圖是：

tanh的程式碼實現：

import numpy as np

def tanh(x):
    s1 = np.exp(x) - np.exp(-x)
    s2 = np.exp(x) + np.exp(-x)
    s = s1 / s2
    return s

為了方便，這裡把x是實數、向量或矩陣的情況一起計算了，呼叫方法如下：

if __name__ == '__main__':
    x = 3
    s = tanh(x)
    print s
    x = np.array([2, 3, 4])
    s = tanh(x)
    print s

以下就是輸出結果：

0.995054753687
[0.96402758 0.99505475 0.9993293 ]

tanh函式的梯度

同樣在這裡我們也要計算tanh函式的梯度，計算公式如下：

tanh_derivative(x)=tanh′(x)=1−tanh2x=1−(ex−e−xex+e−x)2(5)$$\begin{array}{}\text{(5)}& tanh\mathrm{\_}derivative(x)=tan{h}^{\prime }(x)=1-{\tanh }^{2}x=1-{\left(\frac{e^x-e^{-x}}{e^x+e^{-x}}\right)}^2\end{array}$$
Python程式碼實現如下：

import numpy as np

def tanh_derivative(x):
    s1 = np.exp(x) - np.exp(-x)
    s2 = np.exp(x) + np.exp(-x)
    tanh = s1 / s2
    s = 1 - tanh * tanh
    return s

呼叫方法如下：

if __name__ == '__main__':
    x = 3
    s = tanh_derivative(x)
    print s
    x = np.array([2, 3, 4])
    s = tanh_derivative(x)
    print s

輸出結果如下：

0.00986603716544
[0.07065082 0.00986604 0.00134095]

ReLU函式

ReLU是目前深度學習最常用的一個啟用函式，數學公式如下：