深度學習常用啟用函式

在感知器模型、神經網路模型、深度學習模型中均會看見啟用函式的聲影。啟用函式又被稱為轉移函式、激勵函式、傳輸函式或限幅函式，其作用就是將可能的無限域變換到一指定的有限範圍內輸出，這類似於生物神經元具有的非線性轉移特性。

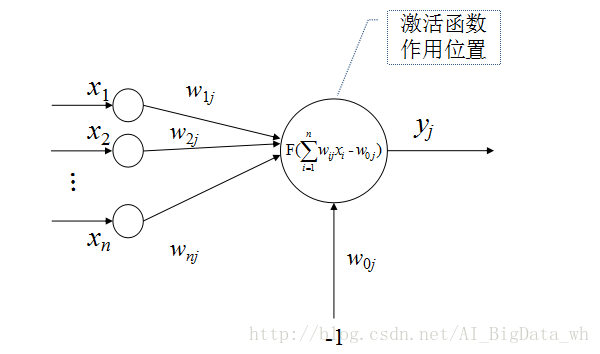
常用的啟用函式有：線性函式、斜坡函式、階躍函式、符號函式、Sigmoid函式、雙曲正切函式、Softplus函式、Softsign函式、Relu函式及其變形、Maxout函式等。

線性函式

線性函式是最簡單的啟用函式：

y=F(x)=kx.
其中y為輸出值，x為輸入訊號的加權和，k是一個常數，表示直線的斜率。
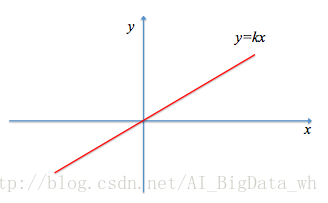
這裡寫圖片描述

在深度學習模型中，線性函式幾乎不被用到。因為其體現不出深度學習模型的價值，如假定深度學習模型有m

層，則最終的輸出為y=kmkm−1...k1x，其等價於單層的線性模型y=k′x（k′=kmkm−1...k1）的輸出。

斜坡函式

斜坡函式的定義如下所示：

y=F(x)=⎧⎩⎨⎪⎪r,x,−r,當x≥r當|x|<r當x≤−r
r和−r分別是處理單元的最大值和最小值，稱為飽和值，一般|r|=1。
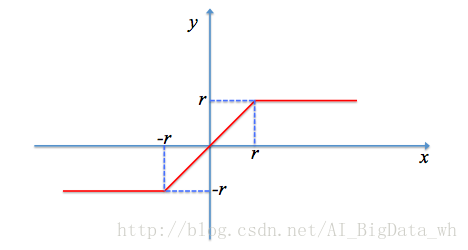
這裡寫圖片描述

階躍函式

階躍函式屬於硬限幅函式的一種：

y=F(x)={1,0,當x>0當x≤0
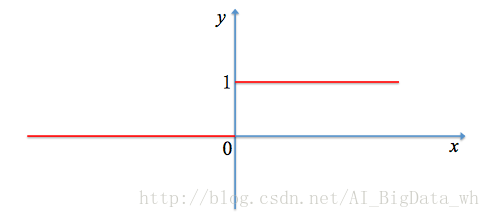
這裡寫圖片描述

符號函式

符號函式也是屬於硬限幅函式的一種，其是根據輸入變數的正負情況決定輸出，若輸入變數為正，則輸出1；若輸入變數為負，則輸出-1；輸入變數為0時可為1或-1：

y=F(x

)={1,−1,當x>0當x≤0
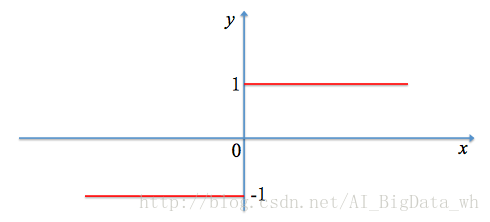
這裡寫圖片描述

注：硬限幅函式雖說簡單直觀，但在深度學習中，很多時候將其應用在隱藏層意義不大，還會適得其反，因此其主要被應用在輸出層。

Sigmoid函式

Sigmoid函式為S型函式的一種，函式的輸出對映在(0,1)之間，單調連續，輸出範圍有限，優化穩定，並且求導容易（因深度學習在更新引數時，常採用梯度下降法，此時需要對啟用函式求導）。但由於其軟飽和性，當|x|≫1時，y趨於0或1，導致其導數無限趨於0，容易產生梯度消失，此時會使訓練出現問題。並且其輸出並不是以0為中心的。

y=F(x)=11+e−x.
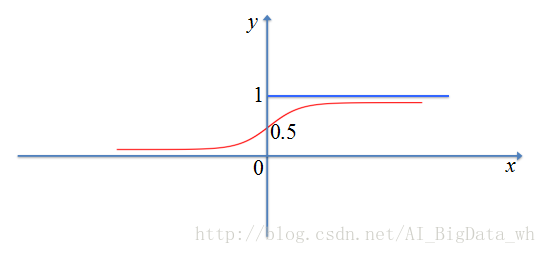
這裡寫圖片描述

注： Sigmoid函式的導數為F′(x)=F(x)(

1−F(x))。

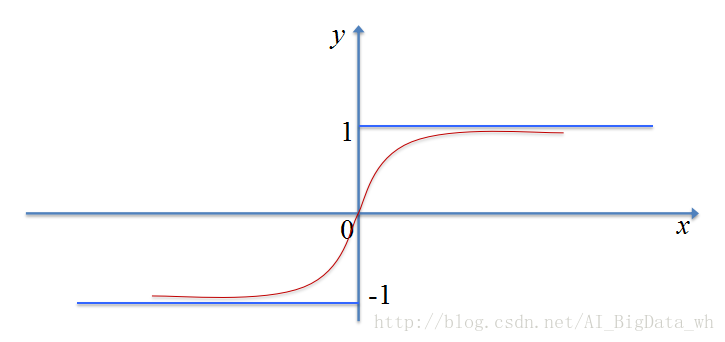
雙曲正切函式

雙曲正切函式（tanh函式）也是S型函式的一種，Sigmoid函式存在的問題它基本上也都存在，不過相對於Sigmoid函式，它是原點對稱的。而且在0周圍，曲線變化趨勢更陡，因此在訓練過程中，權重每次更新的步長更大，能夠更快地收斂到最優值（也可能是區域性最優）。並且當s=0時有y=0，即同時具有雙級輸出。當要求輸出(-1 1)範圍的訊號時，它常被採用。

y=F(x)=ex−e−xex+e−x.
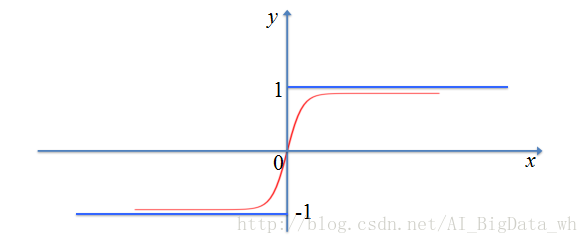
這裡寫圖片描述

注： tanh函式的導數為F′(x)=(1−F(x))2。

Softplus函式

Softplus被定義為：

y=F(x)=log(1+ex).
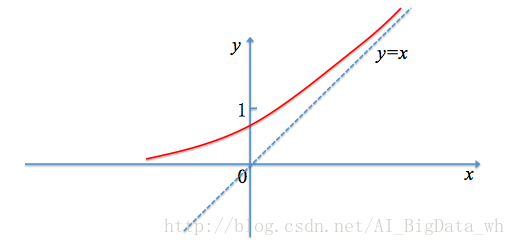
這裡寫圖片描述

Softsign函式

Softsign函式被被定義為：

y=F(x)=x1+|x|.
這裡寫圖片描述

Relu函式及其變形

ReLU是最近幾年非常受歡迎的啟用函式。雖說Sigmoid和tanh效果不錯，但是很容易出現梯度消失現象–當輸入|x|較大時，梯度變得非常小，從而導致SGD收斂速度下降或者無法收斂。ReLU函式被定義為：

y=F(x)=max{0,x}.
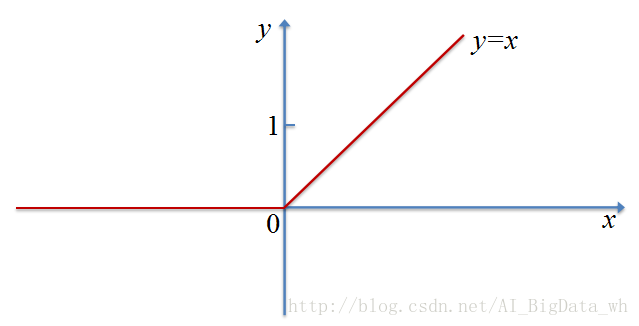
這裡寫圖片描述

不過ReLU也不是十全十美的，觀察其定義便可以發現在x>0時，梯度恆為1，可以保證穩定的下降速度；可當x≤0時，梯度卻恆為0。雖說這樣的特效能強化神經網路的稀疏表達能力，但隨著訓練的進行，可能會出現神經元不可逆轉的死亡，權重從此以後便無法更新。

為了緩解上面的問題，ReLU的變形LReLU、PReLU與RReLU應運而生。其基本思想均是，當x≤0時不再是恆為0輸出，而是為其乘上一個比較小的係數α，因此啟用函式的定義變成：

y=F(x)=

深度學習常用啟用函式

線性函式

斜坡函式

階躍函式