（一）泊松分佈是什麼

泊松分佈是用於近似二項分佈的情況的。二項分佈有兩個引數，一個是事件發生的概率p，一個是試驗的總數n。當p非常小且n也有一定大的時候（n大於等於20，p小於等於0.05），就可以用泊松分佈來近似二項分佈，用泊松分佈來近似二項分佈的好處是計算方便。

（二）泊松分佈公式以及通俗地推導過程

泊松分佈公式：

通俗推導：

假設某一零件廠每天生成的次品數如下：

均值為：

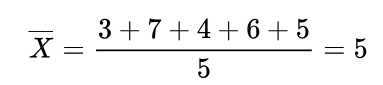
假設我們把每天工廠生產時間設為T：

再把T分為n=4份，並把週一生產出的三個次品放進去：

此時工廠在每個時間段生成次品的概率就如同拋硬幣，要麼出現，要麼不出現，這樣子工廠生產次品的概率符合二項分佈：

但當把資料換成週二的7個次品呢？

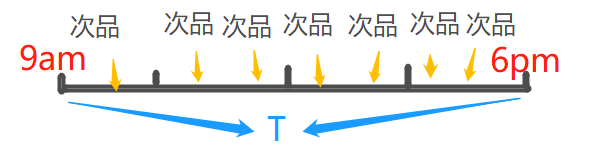
則出現每個時間段多餘一個次品的情況，這樣的話就不符合二項分佈了。要使其符合二項分佈，就必須使n變大，現在讓我們把n=8：

這樣子又能符合二項分佈了：

即只要不出現一個時間段內出現兩個次品的情況，就能用二項分佈解決。

為了達成一個時間段內不出現兩個次品的條件，我們乾脆把n趨向於無窮，因為n越大，T分成的時間段就越多：

更抽象一點，T時間裡出現k個次品的概率為：(式子1)

上式中，n趨於無窮，k是可以確定的，那麼p應該怎麼求呢？

上面的式子1，已經符合二項分佈的，而二項分佈的期望為：

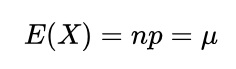
因此：

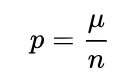----（式子2）

有了式子2後，式子1可以變成：

計算這個極限：

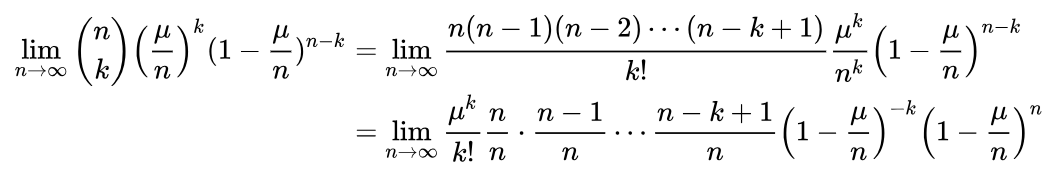
因為當時：

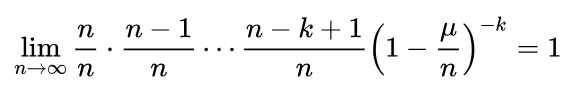
所以：

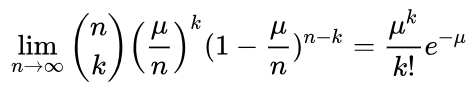
最後把，得到泊松分佈的概率密度函式的公式：

畫出概率密度函式：

當k=8時，綠色部分加起來為0.93，即每天生產次品不超過8個的概率為0.93

（三）總結：

當p十分小且n也比較大的時候可以推薦用泊松分佈（n大於等於20，p小於等於0.05）。

（四）例題分析計算

計算機硬體公司製造某晶片，次品率為0.1%，各晶片稱為次品相互獨立，求在1000個產品中至少有2只次品的概率，以X記產品中的次品數。

解：

用二項分佈：

用泊松分佈計算：

由提：，代入泊松分佈的式子：

顯然用泊松分佈計算方便一點。