在深度網路中，卷積計算應用非常廣泛。在影象處理中，卷積計算也就是影象畫素矩陣與卷積核之間的點對點相乘在累加的運算，但是在不同的深度學習框架或者平臺中，卷積實現的方式有一定的差異，所以我參考一些部落格並根據個人的理解整理了Caffe，Tensorflow及Matlab中的卷積實現。

首先，三者對於影象卷積的基本原理是相同的，不同的只是在矩陣變換的實現上，先回顧下卷積前後影象矩陣大小的變化。

以二維影象矩陣為例，假設有：

• height簡稱h，width簡稱w
• 輸入影象矩陣input_feature：(inputh,inputw)$(inpu{t}_h,inpu{t}_w)$
• 輸出影象矩陣output_feature
  ：(outputh,outputw)$(outpu{t}_h,outpu{t}_w)$
• 卷積核filter：(filterh,filterw)$(filte{r}_h,filte{r}_w)$
• 滑動步長strides：(sh,sw)$(s_h,s_w)$
• padding的長度：(ph,pw)$(p_h,p_w)$

則一般情況下，卷積後的影象矩陣output_feature大小為：

outputh=inputh−filterh+2∗phsh+1outputw=inputw−filterw+2∗pwsw+1$$outpu{t}_h=\frac{inpu{t}_h-filte{r}_h+2\ast p_h}{s_h}+1outpu{t}_w=\frac{inpu{t}_w-filte{r}_w+2\ast p_w}{s_w}+1$$

Caffe的卷積實現

這篇側重在原理的解釋上，原始碼解析沒貼，後面會更新。

Tensorflow的卷積實現

tf.nn.conv2d是TensorFlow裡面實現卷積的函式，函式用法：

tf.nn.conv2d(input, filter, strides, padding, use_cudnn_on_gpu=None, name=None)

# 結果返回一個Tensor，這個輸出就是我們常說的feature map

• 引數Input：卷積的輸入影象，要求是一個4維的Tensor，其大小[batch, in_height, in_width, in_channel]，分別代表輸入圖片的數量，圖片的高度，圖片的寬度，圖片的通道數，這個Tensor的型別是float32或者float64

• 引數filter：相當於CNN中的卷積核，它要求是一個4維的Tensor，其大小[filter_height, filter_width, in_channels, out_channels]，分別代表[卷積核的高度，卷積核的寬度，影象通道數，卷積核個數]，要求型別與引數input相同，有一個地方需要注意，第三維in_channels，就是引數input的第四維

• 引數strides：卷積時在影象每一維的步長，這是一個一維的向量，長度4

• 引數padding：string型別的量，只能是”SAME”,”VALID”其中之一，這個值決定了不同的卷積方式（後面會介紹）

• 引數name：用以指定該操作的name，即該操作的別稱

那麼TensorFlow的卷積具體是怎樣實現的呢，用一些例子去解釋它：

1.考慮一種最簡單的情況，現在有一張3×3單通道的影象（對應的shape：[1，3，3，1]），用一個1×1的卷積核（對應的shape：[1，1，1，1]）去做卷積，最後會得到一張3×3的feature map

2.增加圖片的通道數，使用一張3×3五通道的影象（對應的shape：[1，3，3，5]），用一個1×1的卷積核（對應的shape：[1，1，5，1]）去做卷積，仍然是一張3×3的feature map，這就相當於每一個畫素點，卷積核都與該畫素點的每一個通道做點積

input = tf.Variable(tf.random_normal([1,3,3,5]))
filter = tf.Variable(tf.random_normal([1,1,5,1]))

op = tf.nn.conv2d(input, filter, strides=[1, 1, 1, 1], padding='VALID')

3.把卷積核擴大，現在用3×3的卷積核做卷積，最後的輸出是一個值，相當於情況2的feature map所有畫素點的值求和

input = tf.Variable(tf.random_normal([1,3,3,5]))
filter = tf.Variable(tf.random_normal([3,3,5,1]))

op = tf.nn.conv2d(input, filter, strides=[1, 1, 1, 1], padding='VALID')

4.使用更大的圖片將情況2的圖片擴大到5×5，仍然是3×3的卷積核，令步長為1，輸出3×3的feature map

input = tf.Variable(tf.random_normal([1,5,5,5]))
filter = tf.Variable(tf.random_normal([3,3,5,1]))

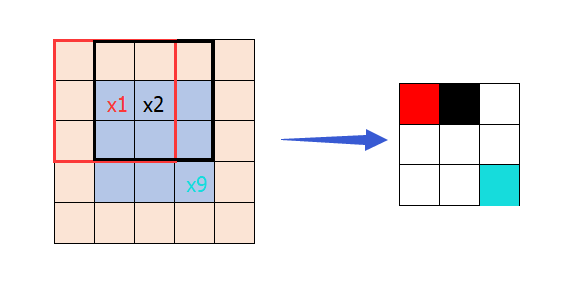
op = tf.nn.conv2d(input, filter, strides=[1, 1, 1, 1], padding='VALID')

注意我們可以把這種情況看成情況2和情況3的中間狀態，在左側圖中卷積核在中間9格中從左往右，從上往下以步長1滑動遍歷，在這些停留的位置上，每停留一個，輸出feature map的一個畫素

5.以上引數padding的值為‘VALID’，當其為‘SAME’時，表示卷積核可以停留在影象邊緣，如下，輸出5×5的feature map

input = tf.Variable(tf.random_normal([1,5,5,5]))
filter = tf.Variable(tf.random_normal([3,3,5,1]))

op = tf.nn.conv2d(input, filter, strides=[1, 1, 1, 1], padding='SAME')

此種方式裡，中間藍色部分是影象本身，外圍灰色是padding的部分，至於會填充多少要根據strides，卷積核尺寸及影象尺寸共同決定，最後滿足的要求是輸出的feature map大小與輸入影象大小一致。

我們希望瞭解卷積中是如何實現兩種padding方式，因此詳細說明一下：
假設有, h代表height，w代表width
輸入Input大小：(inputh,inputw)$(inpu{t}_h,inpu{t}_w)$
卷積核filter大小：(Fh,Fw)$(F_h,F_w)$
滑動步長strides：(Sh,Sw)$(S_h,S_w)$
輸出output大小：(opth,optw)$(op{t}_h,op{t}_w)$
padding大小：(Ph,Pw)$(P_h,P_w)$

padding='VALID'時

卷積核不會超過影象邊緣，也就是說不會在原有輸入的基礎上新增新的元素，輸出矩陣的大小：

opth=⌈inputh−Fh+1Sh⌉optw=⌈inputw−Fw+1Sw⌉$$op{t}_h=\lceil \frac{inpu{t}_h-F_h+1}{S_h}\rceil op{t}_w=\lceil \frac{inpu{t}_w-F_w+1}{S_w}\rceil$$

這個計算方式與上面提到的公式一致，其中⌈x⌉$\lceil x\rceil$表示對