卷積是卷積神經網路的重要組成部分，消耗整個網路中大量計算資源，理解卷積計算過程，對優化網路結構和簡化網路模型非常重要。

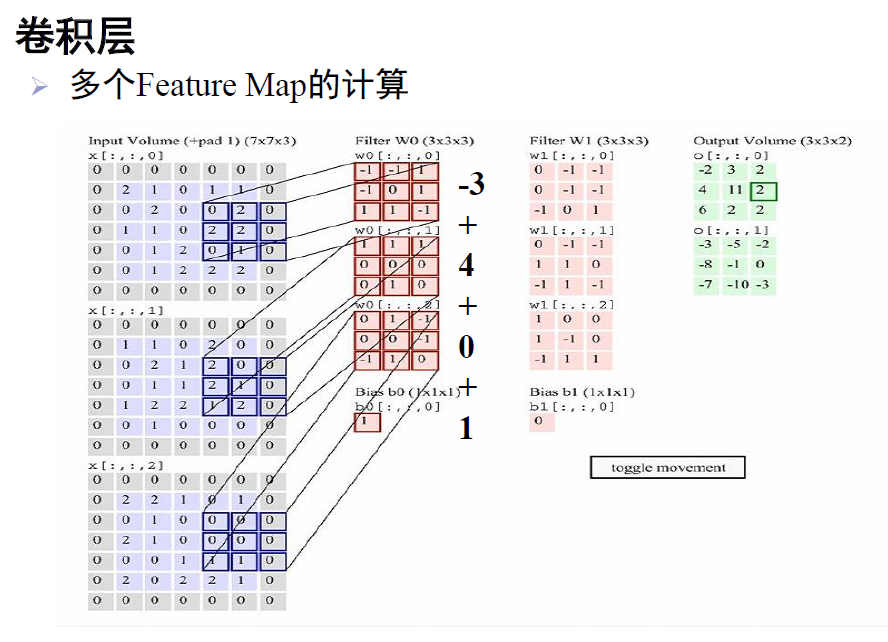
       正常卷積的實現如下圖所示：

        非常重要的是：卷積核其實和特徵圖一樣，是一個三維矩陣，這點需要注意。

       上圖是一個典型的卷積過程。第一列是一個7*7*3的特徵圖；第二列是第一個卷積核，大小為3*3*3；第三列是第二個卷積核，大小為3*3*3；第四列得到了兩個輸出特徵圖，第一個是原特徵圖和第一個卷積核卷積得到的，第二個是原特徵圖和第二個卷積核卷積得到的。

        計算：第二列的卷積核的第一個3*3模板在第一個特徵圖上進行加權迭代，得到值為-3；第二個3*3模組在第二個特徵圖對應位置，進行同樣的操作，得到4；第三個得到0；最後，加上偏置1，即：-3+4+0+1=2。按這樣的計算規則，卷積核在原特徵圖上進行滑動遍歷，最終得到了第四列，第一個輸出特徵圖。第三列的卷積核計算同上，得到了第四列，第二個輸出特徵圖。

        乘法次數：即進行了幾次乘法，第一個卷積核進行了(3*3)*3次乘法，兩個卷積核共2*(3*3)*3次。

        引數個數：即權值個數，第一個卷積核有(3*3)*3個引數，加上一個偏置，共(3*3)*3+1=28個引數。所以，兩個卷積核共28*2=56個引數。

        那麼，卷積過程，在caffe程式碼中是怎麼實現的呢？如下圖所示：

        上圖類似上面的卷積過程，輸入特徵圖大小為：in_channels*in_height_*in_width,卷積核大小為:in_channels*k_height_*k_width（注意：卷積核channels和輸入特徵圖的channels相同

         caffe實現時，先將輸入特徵圖和卷積核都轉化為矩陣，計算好了再還原，如下圖：

       將輸入特徵圖中，卷積部分的那個區域中資料(原特徵圖中)，轉變為一列，如果channels為1，則列長為k_height_*k_width，否則為in_channels*k_height_*k_width。當卷積核移動一次，對應的區域資料又形成了新的一列，卷積核一用移動out_height_*out_width次，這樣輸入特徵圖矩陣的寬度就為out_height_*out_width。所以，就形成了一個(in_channels*k_height_*k_width)*(out