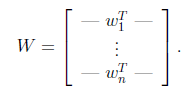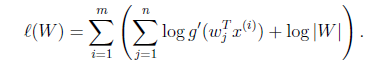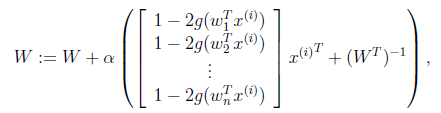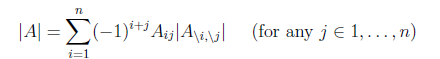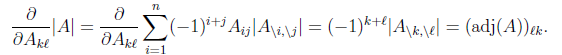1. 問題：

     1、上節提到的PCA是一種資料降維的方法，但是隻對符合高斯分佈的樣本點比較有效，那麼對於其他分佈的樣本，有沒有主元分解的方法呢？

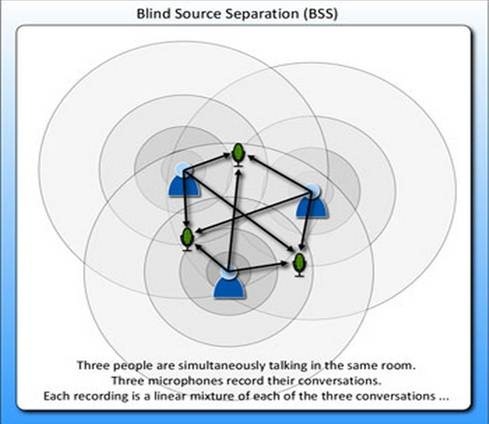
     2、經典的雞尾酒宴會問題（cocktail party problem）。假設在party中有n個人，他們可以同時說話，我們也在房間中一些角落裡共放置了n個聲音接收器（Microphone）用來記錄聲音。宴會過後，我們從n個麥克風中得到了一組資料，i表示取樣的時間順序，也就是說共得到了m組取樣，每一組取樣都是n維的。我們的目標是單單從這m組取樣資料中分辨出每個人說話的訊號。

     將第二個問題細化一下，有n個訊號源，，每一維都是一個人的聲音訊號，每個人發出的聲音訊號獨立。A是一個未知的混合矩陣（mixing matrix），用來組合疊加訊號s，那麼

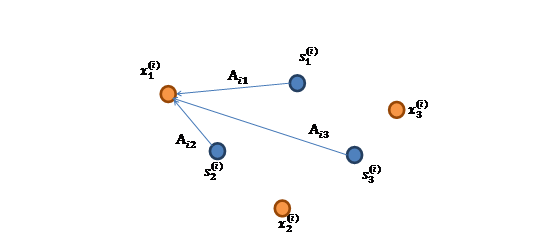
     x的意義在上文解釋過，這裡的x不是一個向量，是一個矩陣。其中每個列向量是，

     表示成圖就是

     這張圖來自

     的每個分量都由的分量線性表示。A和s都是未知的，x是已知的，我們要想辦法根據x來推出s。這個過程也稱作為盲訊號分離。

     令，那麼

     將W表示成

     其中，其實就是將寫成行向量形式。那麼得到：

2. ICA的不確定性（ICA ambiguities）

     由於w和s都不確定，那麼在沒有先驗知識的情況下，無法同時確定這兩個相關引數。比如上面的公式s=wx。當w擴大兩倍時，s只需要同時擴大兩倍即可，等式仍然滿足，因此無法得到唯一的s。同時如果將人的編號打亂，變成另外一個順序，如上圖的藍色節點的編號變為3,2,1，那麼只需要調換A的列向量順序即可，因此也無法單獨確定s。這兩種情況稱為原訊號不確定。

     還有一種ICA不適用的情況，那就是訊號不能是高斯分佈的。假設只有兩個人發出的聲音訊號符合多值正態分佈，，I是2*2的單位矩陣，s的概率密度函式就不用說了吧，以均值0為中心，投影面是橢圓的山峰狀（參見多值高斯分佈）。因為，因此，x也是高斯分佈的，均值為0，協方差為。

     令R是正交陣，。如果將A替換成A’。那麼。s分佈沒變，因此x’仍然是均值為0，協方差。

     因此，不管混合矩陣是A還是A’，x的分佈情況是一樣的，那麼就無法確定混合矩陣，也就無法確定原訊號。

3. 密度函式和線性變換

     在討論ICA具體演算法之前，我們先來回顧一下概率和線性代數裡的知識。

     假設我們的隨機變數s有概率密度函式

     令，首先將式子變換成，然後得到，求解完畢。可惜這種方法是錯誤的。比如s符合均勻分佈的話（），那麼s的概率密度是，現在令A=2，即x=2s，也就是說x在[0,2]上均勻分佈，可知。然而，前面的推導會得到。正確的公式應該是

     推導方法

     更一般地，如果s是向量，A可逆的方陣，那麼上式子仍然成立。

4. ICA演算法

     ICA演算法歸功於Bell和Sejnowski，這裡使用最大似然估計來解釋演算法，原始的論文中使用的是一個複雜的方法Infomax principal。

     我們假定每個有概率密度，那麼給定時刻原訊號的聯合分佈就是

     這個公式代表一個假設前提：每個人發出的聲音訊號各自獨立。有了p(s)，我們可以求得p(x)

     左邊是每個取樣訊號x（n維向量）的概率，右邊是每個原訊號概率的乘積的|W|倍。

     前面提到過，如果沒有先驗知識，我們無法求得W和s。因此我們需要知道，我們打算選取一個概率密度函式賦給s，但是我們不能選取高斯分佈的密度函式。在概率論裡我們知道密度函式p(x)由累計分佈函式（cdf）F(x)求導得到。F(x)要滿足兩個性質是：單調遞增和在[0,1]。我們發現sigmoid函式很適合，定義域負無窮到正無窮，值域0到1，緩慢遞增。我們假定s的累積分佈函式符合sigmoid函式

     求導後

     這就是s的密度函式。這裡s是實數。

     如果我們預先知道s的分佈函式，那就不用假設了，但是在缺失的情況下，sigmoid函式能夠在大多數問題上取得不錯的效果。由於上式中是個對稱函式，因此E[s]=0（s的均值為0），那麼E[x]=E[As]=0，x的均值也是0。

     知道了，就剩下W了。給定取樣後的訓練樣本，樣本對數似然估計如下：

     使用前面得到的x的概率密度函式，得

     大括號裡面是。

     接下來就是對W求導了，這裡牽涉一個問題是對行列式|W|進行求導的方法，屬於矩陣微積分。這裡先給出結果，在文章最後再給出推導公式。

     最終得到的求導後公式如下，的導數為（可以自己驗證）：

     其中是梯度上升速率，人為指定。

     當迭代求出W後，便可得到來還原出原始訊號。

     注意：我們計算最大似然估計時，假設了與之間是獨立的，然而對於語音訊號或者其他具有時間連續依賴特性（比如溫度）上，這個假設不能成立。但是在資料足夠多時，假設獨立對效果影響不大，同時如果事先打亂樣例，並執行隨機梯度上升演算法，那麼能夠加快收斂速度。

     回顧一下雞尾酒宴會問題，s是人發出的訊號，是連續值，不同時間點的s不同，每個人發出的訊號之間獨立（和之間獨立）。s的累計概率分佈函式是sigmoid函式，但是所有人發出聲音訊號都符合這個分佈。A（W的逆陣）代表了s相對於x的位置變化，x是s和A變化後的結果。

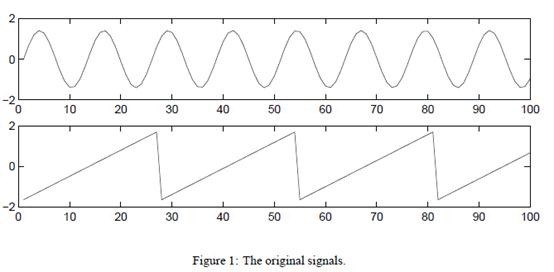
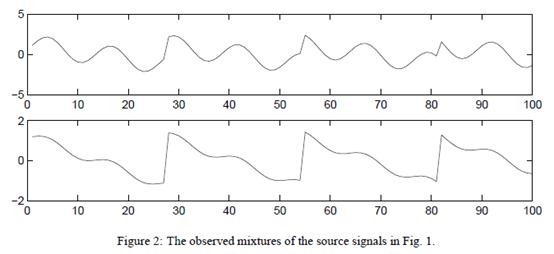
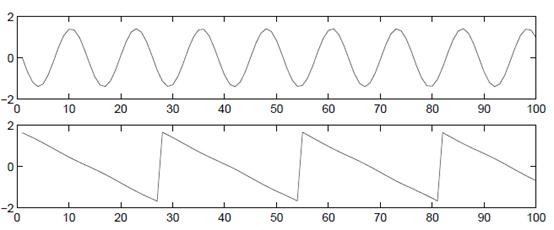
5. 例項

     s=2時的原始訊號

     觀察到的x訊號

     使用ICA還原後的s訊號

6. 行列式的梯度

     對行列式求導，設矩陣A是n×n的，我們知道行列式與代數餘子式有關，

     是去掉第i行第j列後的餘子式，那麼對求導得

     adj(A)跟我們線性代數中學的是一個意思，因此