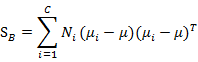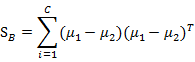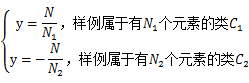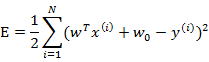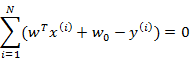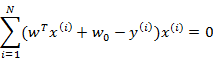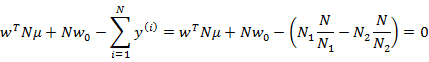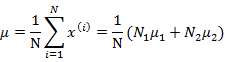線性判別分析(Linear Discriminant Analysis)(二)
4. 例項
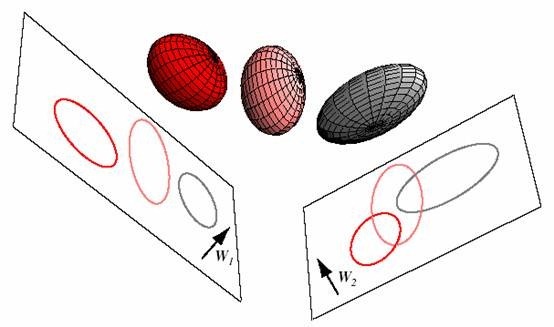
將3維空間上的球體樣本點投影到二維上,W1相比W2能夠獲得更好的分離效果。
PCA與LDA的降維對比:
PCA選擇樣本點投影具有最大方差的方向,LDA選擇分類效能最好的方向。
LDA既然叫做線性判別分析,應該具有一定的預測功能,比如新來一個樣例x,如何確定其類別?
拿二值分來來說,我們可以將其投影到直線上,得到y,然後看看y是否在超過某個閾值y0,超過是某一類,否則是另一類。而怎麼尋找這個y0呢?
看
根據中心極限定理,獨立同分布的隨機變數和符合高斯分佈,然後利用極大似然估計求
然後用決策理論裡的公式來尋找最佳的y0,詳情請參閱PRML。
這是一種可行但比較繁瑣的選取方法,可以看第7節(一些問題)來得到簡單的答案。
5. 使用LDA的一些限制
1、 LDA至多可生成C-1維子空間
LDA降維後的維度區間在[1,C-1],與原始特徵數n無關,對於二值分類,最多投影到1維。
2、 LDA不適合對非高斯分佈樣本進行降維。
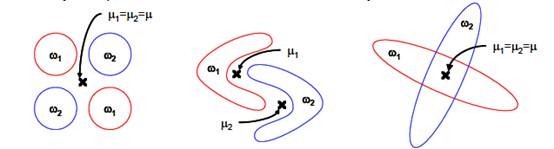
上圖中紅色區域表示一類樣本,藍色區域表示另一類,由於是2類,所以最多投影到1維上。不管在直線上怎麼投影,都難使紅色點和藍色點內部凝聚,類間分離。
3、 LDA在樣本分類資訊依賴方差而不是均值時,效果不好。
上圖中,樣本點依靠方差資訊進行分類,而不是均值資訊。LDA不能夠進行有效分類,因為LDA過度依靠均值資訊。
4、 LDA可能過度擬合數據。
6. LDA的一些變種
1、 非引數LDA
非引數LDA使用本地資訊和K臨近樣本點來計算![]() ,使得
,使得![]() 是全秩的,這樣我們可以抽取多餘C-1個特徵向量。而且投影后分離效果更好。
是全秩的,這樣我們可以抽取多餘C-1個特徵向量。而且投影后分離效果更好。
2、 正交LDA
先找到最佳的特徵向量,然後找與這個特徵向量正交且最大化fisher條件的向量。這種方法也能擺脫C-1的限制。
3、 一般化LDA
引入了貝葉斯風險等理論
4、 核函式LDA
7. 一些問題
上面在多值分類中使用的
是帶權重的各類樣本中心到全樣本中心的雜湊矩陣。如果C=2(也就是二值分類時)套用這個公式,不能夠得出在二值分類中使用的![]() 。
。
對於二值分類問題,令人驚奇的是最小二乘法和Fisher線性判別分析是一致的。
下面我們證明這個結論,並且給出第4節提出的y0值得選取問題。
回顧之前的線性迴歸,給定N個d維特徵的訓練樣例![]() (i從1到N),每個
(i從1到N),每個![]() 對應一個類標籤
對應一個類標籤![]() 。我們之前令y=0表示一類,y=1表示另一類,現在我們為了證明最小二乘法和LDA的關係,我們需要做一些改變
。我們之前令y=0表示一類,y=1表示另一類,現在我們為了證明最小二乘法和LDA的關係,我們需要做一些改變
就是將0/1做了值替換。
我們列出最小二乘法公式
從第一個式子展開可以得到
消元后,得
可以證明第二個式子展開後和下面的公式等價
因此,最後結果仍然是
這個過程從幾何意義上去理解也就是變形後的線性迴歸(將類標籤重新定義),線性迴歸後的直線方向就是二值分類中LDA求得的直線方向w。
好了,我們從改變後的y的定義可以看出y>0屬於類![]() ,y<0屬於類
,y<0屬於類![]() 。因此我們可以選取y0=0,即如果
。因此我們可以選取y0=0,即如果![]() ,就是類
,就是類![]() ,否則是類
,否則是類![]() 。
。
寫了好多,挺雜的,還有個topic模型也叫做LDA,不過名字叫做Latent Dirichlet Allocation,第二作者就是Andrew Ng大牛,最後一個他導師Jordan泰斗了,什麼時候拜讀後再寫篇總結髮上來吧。