使用鄰接矩陣實現圖結構
關於圖的一些特點就不說了,現在我們先展示的是頂點的實現
/**
* Created by 西皮 on 2017/9/15 19:58.
* 圖的頂點類
*/
public class MyVertex<VItem> {
private VItem data;//資料
private int inDegree,outDegree;//出入度數
private VStatus status;//狀態
private long dTime,fTime;//時間標籤
private int parent;//在遍歷樹中的父節點
private int priority;//在遍歷樹中的優先順序 這裡的屬性,status使用的enum來標識的,三種頂點狀態,分別是UNDISCOVERED,DISCOVERED,VISITED,分別用來表示未被發現,已被發現但是還未訪問完畢,已經被訪問完畢
/**
* Created by 西皮 on 2017/9/16 9:49.
* 定義頂點狀態的列舉類
*/
public enum VStatus {
UNDISCOVERED("UNDISCOVERED"),DISCOVERED("DISCOVERED"),VISITED("VISITED");
private final String value;
VStatus(String value){
this.value = value;
}
public String getValue() {
return value;
}
}接下來展示邊
/**
* Created by 西皮 on 2017/9/16 10:09.
* 圖的邊類
*/
public class MyEdge<EItem> {
private EItem data;//資料
private int weight;//權重
private EType type;//在便利書中所屬的型別
public MyEdge(EItem data,int weight){
this.data = data;
this.weight = weight;
this.type = EType.UNDETERMINED;
}
public EItem getData() {
return data;
}
public void setData(EItem data) {
this.data = data;
}
public int getWeight() {
return weight;
}
public void setWeight(int weight) {
this.weight = weight;
}
public EType getType() {
return type;
}
public void setType(EType type) {
this.type = type;
}
}
這裡的邊同樣使用enum來表示邊的狀態
/**
* Created by 西皮 on 2017/9/16 9:55.
* 定義邊狀態的列舉類
*/
public enum EType {
UNDETERMINED("UNDETERMINED"),TREE("TREE"),
CROSS("CROSS"),FORWARD("FORWARD"),BACKWARD("BACKWARD");
private final String value;
EType(String value){
this.value = value;
}
public String getValue(){
return value;
}
} UNDETERMINED圖初始化時,所有邊預設是UNDETERMINED,其他的邊狀態需要結合圖的BFS和DFS來看,更簡單,這裡我們暫且放一邊。
接下來,我們來實現一個圖
import java.util.ArrayList;
import java.util.Date;
import java.util.List;
/**
* Created by 西皮 on 2017/9/16 10:13.
* 矩陣圖
*/
public class MyGrapMatrix<VItem,EItem> {
private List<MyVertex<VItem>> V = new ArrayList<>();//頂點集
private List<List<MyEdge<EItem>>> E = new ArrayList<>();//邊集,使用一個鄰接矩陣來表示邊
private int n;//頂點數量
private int e;//邊的數量
public MyGrapMatrix(){}
public VItem getMyVertex(int i){
return V.get(i).getData();//獲得資料
}
public int getMyVertexInDegree(int i){
return V.get(i).getInDegree();//獲得頂點入度
}
public int getMyVertexOutDegree(int i){
return V.get(i).getOutDegree();
}
public VStatus getMyVertexStatus(int i){
return V.get(i).getStatus();
}
public int getVertexNum(){
return n;
}
public int getEdgeNum(){
return e;
}
public long getMyVertexDTime(int i){
return V.get(i).getdTime();
}
public long getMyVertexFTime(int i){
return V.get(i).getfTime();
}
public int getMyVertexParent(int i){
return V.get(i).getParent();
}
public int getMyVertexPriority(int i){
return V.get(i).getPriority();
}
/**
* 獲得當前節點i的比j小的下一個鄰居
* @param i
* @param j
* @return
*/
public int nextNbr(int i,int j){
while (-1 < j && !exisits(i,--j));
return j;
}
/**
* 獲得頂點i的首個鄰居
* @param i
* @return
*/
public int firstNbr(int i){
return nextNbr(i,V.size());
}
/**
* 判斷兩個頂點是否有邊
* @param i
* @param j
* @return
*/
public boolean exisits(int i,int j){
if((0 <= i) && (i < n) &&
(0 <= j) && (j < n) &&
(E.get(i).get(j) != null))
return true;
return false;
}
/**
* 獲得邊(i,j)的資料
* @param i
* @param j
* @return
*/
public EItem getMyEdgeData(int i,int j){
return E.get(i).get(j).getData();
}
public EType getMyEdgeStatus(int i,int j){
return E.get(i).get(j).getType();
}
public int getMyEdgeWeight(int i,int j){
return E.get(i).get(j).getWeight();
}
/**
* 插入一條邊,邊的兩個頂點分別是i和j
* @param edgeData
* @param weight
* @param i
* @param j
*/
public void insertEdge(EItem edgeData,int weight,int i,int j){
if (exisits(i,j)) return;//忽略已有的邊
E.get(i).set(j,new MyEdge<EItem>(edgeData,weight));
e++;//更新邊計數
//更新關聯頂點i的出度和j的入度
V.get(i).setOutDegree(V.get(i).getOutDegree()+1);
V.get(j).setInDegree(V.get(j).getInDegree()+1);
}
/**
* 刪除邊(i,j)
* @param i
* @param j
* @return
*/
public EItem removeEdge(int i,int j){
EItem eBak = getMyEdgeData(i,j);
E.get(i).set(j,null);//刪除邊(i,j)
e--;//更新邊計數
V.get(i).setOutDegree(V.get(i).getOutDegree()-1);
V.get(j).setInDegree(V.get(j).getInDegree()-1);
return eBak;
}
/**
* 頂點插入
* @param vertexData
* @return
*/
public int insertVertex(VItem vertexData){
for (int j = 0;j < n;j++) E.get(j).add(null);
n++;
ArrayList<MyEdge<EItem>> lineEdges = new ArrayList<>(n);
for (int i = 0;i < n;i++){
lineEdges.add(null);
}
E.add(lineEdges);
V.add(new MyVertex<VItem>(vertexData));
return n-1;
}
/**
* 刪除頂點及其關聯邊,返回該頂點資訊
* @param i
* @return
* 索引所對應的頂點就改變了
*/
public VItem removeVertex(int i){
for (int j = 0;j < n;j++){
if(exisits(i,j)){
removeEdge(i,j);
}
}
E.remove(i);n--;//刪除第i行
VItem vBak = V.get(i).getData();V.remove(i);//備份之後,刪除頂點i
for (int j = 0;j < n;j++){//刪除所有入邊及第i列
E.get(j).remove(i);
V.get(j).setOutDegree(V.get(j).getOutDegree()-1);
}
return vBak;//返回被刪除頂點的資訊
}
private int BFSclock = 0;
/**
* 廣度優先搜尋Breadth-First Search
* @param v
*/
public void BFS(int v){
MyQueue<Integer> Q = new MyQueue<>();
V.get(v).setStatus(VStatus.DISCOVERED);
Q.enqueue(v);
while (!Q.isEmpty()){
v = Q.dequeue();
System.out.println(V.get(v).getData());
V.get(v).setdTime(++BFSclock);//取出對首頂點v,並給個時間戳
//考察v的每一個鄰居u
for (int u = firstNbr(v);-1 < u; u = nextNbr(v,u)){
if (VStatus.UNDISCOVERED == V.get(u).getStatus()){
//若u尚未被發現
V.get(u).setStatus(VStatus.DISCOVERED);
Q.enqueue(u);//發現該頂點
//將他們之間的邊設定為TREE邊
E.get(v).get(u).setType(EType.TREE);
//把u在遍歷樹中的父節點設定成v
V.get(u).setParent(v);
}else {
E.get(v).get(u).setType(EType.CROSS);
}
}
//至此,當前頂點訪問完畢
V.get(v).setStatus(VStatus.VISITED);
}
}
/**
* @param s
*/
public void bfs(int s){//s為初始頂點
BFSclock = 0;
int v = s;
do {
if(VStatus.UNDISCOVERED == V.get(v).getStatus())
BFS(v);//即從該頂點出發啟動一次BFS
}while (s != (v = (++v % n)));
}
private int DFSclock = 0;
/**
* 深度優先遍歷
* @param v
*/
public void DFS(int v){
V.get(v).setdTime(++DFSclock);
V.get(v).setStatus(VStatus.DISCOVERED);//發現當前頂點v
System.out.println(V.get(v).getData());
for (int u = firstNbr(v); -1 < u; u = nextNbr(v,u)){//列舉v的每一鄰居u
switch (V.get(u).getStatus()){//並視其狀態分別處理
case UNDISCOVERED://u尚未發現,意味著支撐樹可在此擴充套件
E.get(v).get(u).setType(EType.TREE);
V.get(u).setParent(v);
DFS(u);
break;
case DISCOVERED://u已被發現但尚未訪問完畢,應屬被後代指向的祖先
E.get(v).get(u).setType(EType.BACKWARD);
break;
default://u已訪問完畢(VISITED,有向圖),則視承襲關係分為前向邊或跨邊
E.get(v).get(u).setType(V.get(v).getdTime()<V.get(u).getdTime()?EType.FORWARD:EType.CROSS);
break;
}//switch
}
V.get(v).setStatus(VStatus.VISITED);
V.get(v).setfTime(++DFSclock);//至此,當前頂點v方告訪問完畢
}
public void dfs(int s){//s為初始頂點
DFSclock = 0;
int v = s;
do {
if(VStatus.UNDISCOVERED == V.get(v).getStatus())
DFS(v);//即從該頂點出發啟動一次BFS
}while (s != (v = (++v % n)));
}
}
頂點集使用一個ArrayList,這是一個數組,使用它的索引來標識不同的頂點,而邊則使用的是一個二維陣列來來表示,這樣會使他的空間複雜度為Θ(n^2)。
這個導致這種結構所使用儲存空間和這個圖的邊數沒有關係,所以像這樣使用鄰接矩陣實現的圖更適合稠密圖。
在這裡我們首先看看這裡的exists()方法
/**
* 判斷兩個頂點是否有邊
* @param i
* @param j
* @return
*/
public boolean exisits(int i,int j){
if((0 <= i) && (i < n) &&
(0 <= j) && (j < n) &&
(E.get(i).get(j) != null))
return true;
return false;
}我們首先需要確定i和j這兩個表示頂點的序號是可用的,然後在去表示邊的矩陣中查詢從i指向j的這條邊是否存在,也就是我們是否把MyEdge的物件存放進這個矩陣中,為null則不存在,否則存在。
接下來,我們來看看firstNbr(int i)和nextNbr(int i)這兩個方法
/**
* 獲得當前節點i的比j小的下一個鄰居
* @param i
* @param j
* @return
*/
public int nextNbr(int i,int j){
while (-1 < j && !exisits(i,--j));
return j;
}
/**
* 獲得頂點i的首個鄰居
* @param i
* @return
*/
public int firstNbr(int i){
return nextNbr(i,V.size());
}呼叫firstNbr()可以獲得i頂點的從尾部開始的第一個鄰居,而nextNbr()可以循著這個方向向前再找一個新鄰居,這裡在遍歷中時非常有用的。
接下來是對圖的動態操作,分別為對邊的新增刪除,和對頂點的新增刪除,邊的新增刪除沒什麼問題,看看程式碼就夠了,這裡我們著重看一看頂點的新增刪除
/**
* 頂點插入
* @param vertexData
* @return
*/
public int insertVertex(VItem vertexData){
for (int j = 0;j < n;j++) E.get(j).add(null);
n++;
ArrayList<MyEdge<EItem>> lineEdges = new ArrayList<>(n);
for (int i = 0;i < n;i++){
lineEdges.add(null);
}
E.add(lineEdges);
V.add(new MyVertex<VItem>(vertexData));
return n-1;
}
/**
* 刪除頂點及其關聯邊,返回該頂點資訊
* @param i
* @return
* 索引所對應的頂點就改變了
*/
public VItem removeVertex(int i){
for (int j = 0;j < n;j++){
if(exisits(i,j)){
removeEdge(i,j);
}
}
E.remove(i);n--;//刪除第i行
VItem vBak = V.get(i).getData();V.remove(i);//備份之後,刪除頂點i
for (int j = 0;j < n;j++){//刪除所有入邊及第i列
E.get(j).remove(i);
V.get(j).setOutDegree(V.get(j).getOutDegree()-1);
}
return vBak;//返回被刪除頂點的資訊
} 頂點新增時,我們首先需要對應的在表示邊的矩陣中新增一列和一行,因為這兩個V頂點集和E邊集是對應的,所以我們看到首先遍歷每一行,為每一行新增一個為null的邊也就是這兩個頂點間的邊還不存在,讓頂點的數量n++;再接下來,我們為這個矩陣新增一行資料,當然這一行資料存放的也全是空,因為這個新頂點還沒有與任何頂點關聯。最後我們把這個新頂點放在V集的末尾。
此時,我們可以看到儘管我們對陣列做了這麼多動態操作,但實質上這些資料全是直接新增在陣列的最後一個位置,這個操作的時間複雜度是Ο(1)也就是常數時間。
public boolean add(E e) {
ensureCapacityInternal(size + 1); // Increments modCount!!
elementData[size++] = e;
return true;
}這個是add(E e)的實際操作,我們可以看到,他首先判斷容量是否足夠,不夠就擴容,夠就直接把資料存放在最後,然後size++
那麼刪除時也是同理,但是刪除的時間複雜度就與他的i有關係了,因為i後面的元素需要前移,同時又因為是一個二維陣列的,這裡時間複雜度應該是Ο(n^2),其他就是類似的操作了,這裡就不再說了。
最後測試一下個圖是否正確
@Test
public void testGraphBFS(){
MyGrapMatrix<String,Integer> myGrapMatrix = new MyGrapMatrix<>();
myGrapMatrix.insertVertex("S");
myGrapMatrix.insertVertex("A");
myGrapMatrix.insertVertex("D");
myGrapMatrix.insertVertex("E");
myGrapMatrix.insertVertex("C");
myGrapMatrix.insertVertex("B");
myGrapMatrix.insertVertex("F");
myGrapMatrix.insertVertex("G");
myGrapMatrix.insertEdge(1,1,0,1);
myGrapMatrix.insertEdge(1,1,0,4);
myGrapMatrix.insertEdge(1,1,0,2);
myGrapMatrix.insertEdge(1,1,1,0);
myGrapMatrix.insertEdge(1,1,1,4);
myGrapMatrix.insertEdge(1,1,1,3);
myGrapMatrix.insertEdge(1,1,2,0);
myGrapMatrix.insertEdge(1,1,2,5);
myGrapMatrix.insertEdge(1,1,3,1);
myGrapMatrix.insertEdge(1,1,3,6);
myGrapMatrix.insertEdge(1,1,3,7);
myGrapMatrix.insertEdge(1,1,4,0);
myGrapMatrix.insertEdge(1,1,4,1);
myGrapMatrix.insertEdge(1,1,4,5);
myGrapMatrix.insertEdge(1,1,5,2);
myGrapMatrix.insertEdge(1,1,5,4);
myGrapMatrix.insertEdge(1,1,6,3);
myGrapMatrix.insertEdge(1,1,6,7);
myGrapMatrix.insertEdge(1,1,7,3);
myGrapMatrix.insertEdge(1,1,7,5);
myGrapMatrix.insertEdge(1,1,7,6);
System.out.println(myGrapMatrix.getVertexNum());
System.out.println(myGrapMatrix.getEdgeNum());
myGrapMatrix.BFS(0);
} 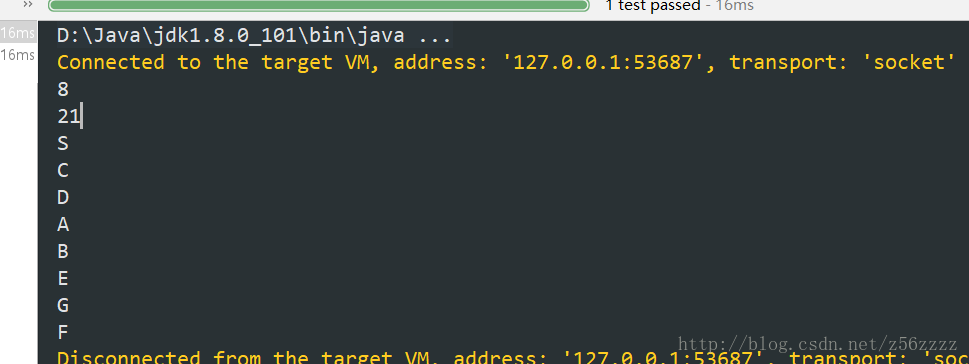
這裡同時測試了樹的BFS,確實我們完成樹的同時也順便完成樹的DFS和BFS,這些東西,以後再說。
