基於粒子濾波的SLAM(GMapping)演算法分析
阿新 • • 發佈:2019-02-03
本文是《Improved Techniques for Grid Mapping_with Rao-Blackwellized Particle Filters》的大致翻譯,難免有不通順與錯誤的地方,如有錯誤請指出,謝謝!
設想一個機器人在一個未知環境中移動,其目的是獲得當前環境的地圖。地圖可以用一個儲存每個網格單元顏色的矩陣表示,單元格的顏色只能為黑色或白色。由於感測器與電機都存在誤差,運動很可能偏離目標方向,因此機器人很容易“迷路”。所以同步定位與地圖構建(SLAM)問題總是被稱作“雞和蛋”的問題:機器人首先需要知道自身的位置去獲得一個準確的地圖,但是獲取地圖同樣也需要一個準確的定位。定位與地圖估計之間的相互依賴使SLAM問題變得非常困難,並且通常需要在高維空間中搜索解決方案。
很多學者對SLAM問題進行了廣泛的研究。在2000年,Murphy應用Rao-Blackwellized粒子濾波演算法去解決SLAM問題。Rao-Blackwellized的主要方式是用許多粒子去獲取準確的地圖。因此減少粒子的數量是優化這一演算法的主要挑戰。
1 地圖構建中的Rao-Blackwellized粒子濾波演算法
SLAM的核心思想是根據其觀測值和其里程計測量資訊去估計聯合後驗概率密度函式(代表地圖中的點、代表機器人的軌跡)。可以看出,軌跡和地圖需要同時計算出來,這樣的計算很複雜而且計算的結果可能不收斂。而RBPF(Rao-Blackwellized Particle Filter)演算法利用公式(1)對聯合概率密度函式進行因式分解。
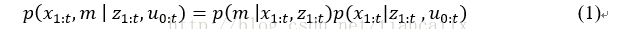
因此RBPF可以先估計機器人的軌跡而後再去根據已知的軌跡計算地圖。由地圖的概率密度函式可以看出,地圖強烈依賴於機器人的位姿,所以這個方法是可行的。
地圖的概率密度函式可以通過已知位姿的建圖方法“mapping with known poses”來計算。後驗概率密度函式應用粒子濾波來估計。
粒子濾波演算法的核心思想是利用一系列隨機樣本的加權和近似後驗概率密度函式,通過求和來近似積分操作。該演算法源於Monte Carlo思想,即以某事件出現的頻率來指代該事件的概率。因此在濾波過程中,需要用到概率的地方,一概對變數取樣,以大量取樣及其相應的權值來近似表示概率密度函式。
其中最普遍的粒子濾波演算法為SIR(Samping Importance Resampling)濾波器。該演算法通過以下四步完成:
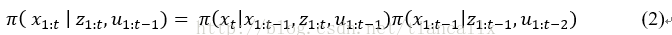
根據等式2,權值可通過以下公式計算
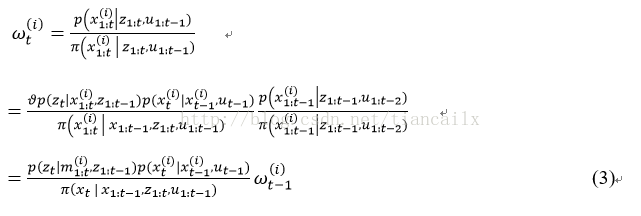
Doucet等學者基於RBPF演算法提出了改進的重要性概率密度函式並且增加了自適應重取樣技術。如上一節所述,為了獲得下一迭代步驟的粒子取樣我們需要在預測階段從重要性概率密度函式中抽取樣本。顯然,重要性概率密度函式越接近目標分佈,濾波器的效果越好。

為了克服這個問題,可以在生成下一次採用時將最近的觀測考慮進去。通過將整合到概率分佈中,可以將抽樣集中在觀測似然的有意義的區域。為此Doucet等提出了最優重要性概率密度函式,式4為粒子權重方差的最優分佈。
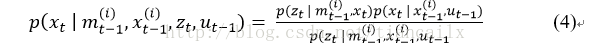
所以式(4)在機器人裝備鐳射測距儀的時候非常適用。
現在的RBPF演算法過程是這樣的,首先根據運動模型對機器人下一時刻位姿進行預測,得到預測的狀態值並且對其進行取樣。第二步是通過最優概率密度函式(4)對各個粒子進行權值的計算。之後進行重取樣,根據粒子的權重重新分佈粒子,為下次預測提供輸入。最後,根據粒子的軌跡計算地圖的後驗概率密度函式。


圖2中展示了在不同場景下的粒子分佈情況。(a)為在開放的走廊中,粒子沿著走廊分佈。(b)為在死衚衕中,粒子分佈的不確定性很小,分佈的很集中。(c)為根據里程計運動模型預測生成的粒子分佈,分佈的很分散。
因此,該演算法將最近的里程計資訊與觀測資訊同時併入重要性概率密度函式中,使用匹配掃描過程來確定觀察似然函式的分佈區域,這樣就把取樣的重點集中在可能性更高的區域。當由於觀察不佳或者當前掃描與先前計算的地圖重疊區域太小而失敗時,將會用圖2中(c)所示的里程計運動模型作為重要性概率密度函式。
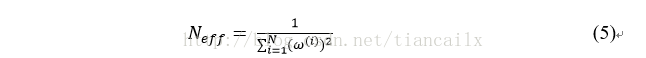
這裡的為粒子的歸一化權值。
Doucet等為了減少進行重取樣步驟的次數,提出了一種理論判定方法來判定是否需要進行重取樣。只有當下降到閾值(,為粒子數)以下時,才進行一次重取樣。由於重取樣只在需要時進行,進行重取樣的次數將大大減少。多次的實驗證明了這種方法大大降低了將好粒子濾去的風險。
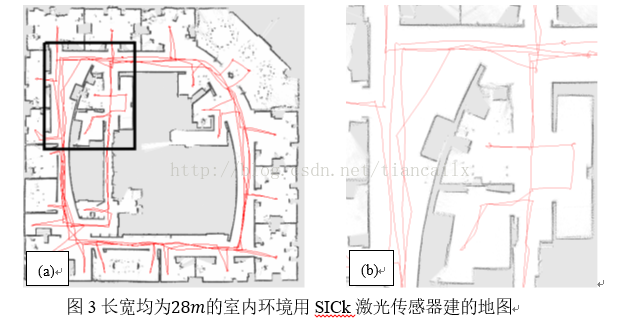

圖3的(a)圖是通過配有SICK鐳射感測器的先鋒2(Pioneer 2)機器人在長寬均為28m的室內環境中構建的地圖。圖3的(b)圖顯示了該地圖的放大細節,展示了該演算法建圖的準確性。
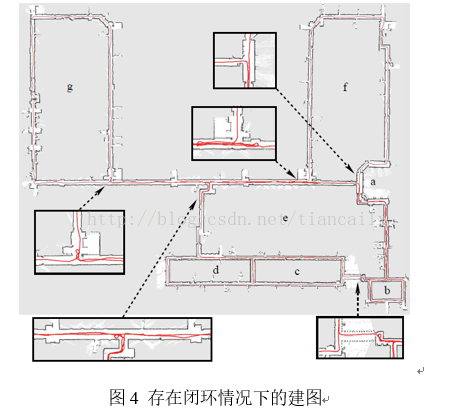

圖4顯示了包含幾個巢狀閉環的室內環境。在這種環境下地圖構建非常困難,閉環增加了Rao-Blackwellized粒子濾波器粒子耗盡的機率。圖4展示了RBPF演算法在使用60個粒子時可以生成一致並且準確的地圖,然而,此時產生的地圖有時會產生雙層牆壁。
設想一個機器人在一個未知環境中移動,其目的是獲得當前環境的地圖。地圖可以用一個儲存每個網格單元顏色的矩陣表示,單元格的顏色只能為黑色或白色。由於感測器與電機都存在誤差,運動很可能偏離目標方向,因此機器人很容易“迷路”。所以同步定位與地圖構建(SLAM)問題總是被稱作“雞和蛋”的問題:機器人首先需要知道自身的位置去獲得一個準確的地圖,但是獲取地圖同樣也需要一個準確的定位。定位與地圖估計之間的相互依賴使SLAM問題變得非常困難,並且通常需要在高維空間中搜索解決方案。
很多學者對SLAM問題進行了廣泛的研究。在2000年,Murphy應用Rao-Blackwellized粒子濾波演算法去解決SLAM問題。Rao-Blackwellized的主要方式是用許多粒子去獲取準確的地圖。因此減少粒子的數量是優化這一演算法的主要挑戰。
1 地圖構建中的Rao-Blackwellized粒子濾波演算法
SLAM的核心思想是根據其觀測值和其里程計測量資訊去估計聯合後驗概率密度函式(代表地圖中的點、代表機器人的軌跡)。可以看出,軌跡和地圖需要同時計算出來,這樣的計算很複雜而且計算的結果可能不收斂。而RBPF(Rao-Blackwellized Particle Filter)演算法利用公式(1)對聯合概率密度函式進行因式分解。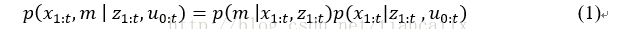
因此RBPF可以先估計機器人的軌跡而後再去根據已知的軌跡計算地圖。由地圖的概率密度函式可以看出,地圖強烈依賴於機器人的位姿,所以這個方法是可行的。
地圖的概率密度函式可以通過已知位姿的建圖方法“mapping with known poses”來計算。後驗概率密度函式應用粒子濾波來估計。
粒子濾波演算法的核心思想是利用一系列隨機樣本的加權和近似後驗概率密度函式,通過求和來近似積分操作。該演算法源於Monte Carlo思想,即以某事件出現的頻率來指代該事件的概率。因此在濾波過程中,需要用到概率的地方,一概對變數取樣,以大量取樣及其相應的權值來近似表示概率密度函式。
其中最普遍的粒子濾波演算法為SIR(Samping Importance Resampling)濾波器。該演算法通過以下四步完成:
1)預測階段:粒子濾波首先根據狀態轉移函式預測生成大量的取樣,這些取樣就稱之為粒子,利用這些粒子的加權和來逼近後驗概率密度。
2)校正階段:隨著觀測值的依次到達,為每個粒子計算相應的重要性權值。這個權值代表了預測的位姿取第個粒子時獲得觀測的概率。如此這般下來,對所有粒子都進行這樣一個評價,越有可能獲得觀測的粒子,獲得的權重越高。
3)重取樣階段:根據權值的比例重新分佈取樣粒子。由於近似逼近連續分佈的粒子數量有限,因此這個步驟非常重要。下一輪濾波中,再將重取樣過後的粒子集輸入到狀態轉移方程中,就能夠獲得新的預測粒子了。
4)地圖估計:對於每個取樣的粒子,通過其取樣的軌跡與觀測計算出相應的地圖估計。
SIR演算法需要在新的觀測值到達時從頭評估粒子的權重。當軌跡的長度隨著時間的推移而增加時,這個過程的計算複雜度將越來越高。因此Doucet等學者通過式(2)限制重要性概率密度函式來獲得遞迴公式去計算重要性權值。
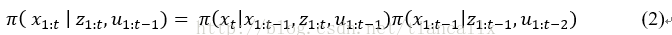
根據等式2,權值可通過以下公式計算
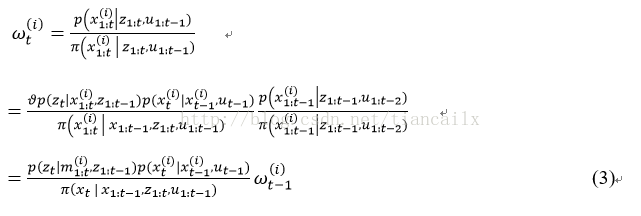
2 GMapping中的優化演算法
GMapping為2007年在ROS中開源的SLAM軟體包,是目前使用最廣泛的軟體包。它可用於室內和室外,應用改進的自適應RBPF演算法來進行定位與建圖。Doucet等學者基於RBPF演算法提出了改進的重要性概率密度函式並且增加了自適應重取樣技術。如上一節所述,為了獲得下一迭代步驟的粒子取樣我們需要在預測階段從重要性概率密度函式中抽取樣本。顯然,重要性概率密度函式越接近目標分佈,濾波器的效果越好。
2.1 最優重要性概率密度函式
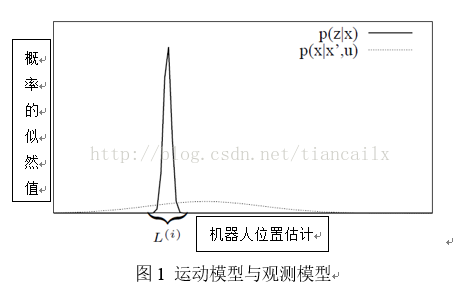
典型的粒子濾波器應用里程計運動模型作為重要性概率密度函式。這種運動模型的計算非常簡單,並且權值只根據觀測模型即可算出。然而,這種模型並不是最理想的。當機器人裝備鐳射雷達(如SICK,Hokuyo等)時,鐳射測得的資料比里程計精確的多,因此使用觀測模型作為重要性概率密度函式將要準確的多。圖1展示了觀測模型的分佈明顯小於運動模型的分佈。由於觀測模型的分佈區域很小,樣本處在觀測的分佈(圖中的區域)的機率很小,在保證充分覆蓋觀測的分佈情況下所需要的粒子數就會變得很多,這將會導致使用運動模型作為重要性概率密度函式類似的問題:需要大量的樣本來充分覆蓋分佈的區域。
為了克服這個問題,可以在生成下一次採用時將最近的觀測考慮進去。通過將整合到概率分佈中,可以將抽樣集中在觀測似然的有意義的區域。為此Doucet等提出了最優重要性概率密度函式,式4為粒子權重方差的最優分佈。
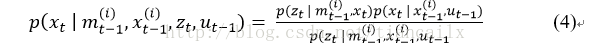
所以式(4)在機器人裝備鐳射測距儀的時候非常適用。
現在的RBPF演算法過程是這樣的,首先根據運動模型對機器人下一時刻位姿進行預測,得到預測的狀態值並且對其進行取樣。第二步是通過最優概率密度函式(4)對各個粒子進行權值的計算。之後進行重取樣,根據粒子的權重重新分佈粒子,為下次預測提供輸入。最後,根據粒子的軌跡計算地圖的後驗概率密度函式。

圖2中展示了在不同場景下的粒子分佈情況。(a)為在開放的走廊中,粒子沿著走廊分佈。(b)為在死衚衕中,粒子分佈的不確定性很小,分佈的很集中。(c)為根據里程計運動模型預測生成的粒子分佈,分佈的很分散。
因此,該演算法將最近的里程計資訊與觀測資訊同時併入重要性概率密度函式中,使用匹配掃描過程來確定觀察似然函式的分佈區域,這樣就把取樣的重點集中在可能性更高的區域。當由於觀察不佳或者當前掃描與先前計算的地圖重疊區域太小而失敗時,將會用圖2中(c)所示的里程計運動模型作為重要性概率密度函式。
2.2 自適應重取樣
對粒子濾波的效能具有重要影響的另一個因素是重取樣步驟。在重取樣期間,低權值的粒子通常由高權值的取樣代替。由於用來逼近目標分佈使用的粒子數量是有限的,所以重取樣步驟非常重要。重取樣步驟也可能把一些好的粒子濾去,隨著的進行,粒子的數目會逐漸減少,最後導致粒子耗盡使該演算法失效。通常採用有效粒子數來衡量粒子權值的退化程度,即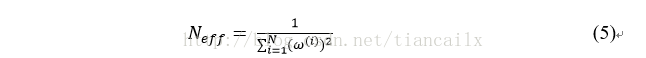
這裡的為粒子的歸一化權值。
Doucet等為了減少進行重取樣步驟的次數,提出了一種理論判定方法來判定是否需要進行重取樣。只有當下降到閾值(,為粒子數)以下時,才進行一次重取樣。由於重取樣只在需要時進行,進行重取樣的次數將大大減少。多次的實驗證明了這種方法大大降低了將好粒子濾去的風險。
3 實驗

圖3的(a)圖是通過配有SICK鐳射感測器的先鋒2(Pioneer 2)機器人在長寬均為28m的室內環境中構建的地圖。圖3的(b)圖顯示了該地圖的放大細節,展示了該演算法建圖的準確性。

圖4顯示了包含幾個巢狀閉環的室內環境。在這種環境下地圖構建非常困難,閉環增加了Rao-Blackwellized粒子濾波器粒子耗盡的機率。圖4展示了RBPF演算法在使用60個粒子時可以生成一致並且準確的地圖,然而,此時產生的地圖有時會產生雙層牆壁。
4總結
本文介紹了一種由Doucet等提出的改進Rao-Blackwellized粒子濾波器構建柵格地圖的演算法。該方法基於最近的感測器資訊,測距和掃描匹配過程的觀測似然函式來計算高精度的後驗概率密度函式。改進演算法比原始演算法應用了更少的粒子來構建地圖,並且使用了一種更準確的方式分佈取樣粒子。此外,該演算法使用了基於有效樣本量的自適應重取樣策略。該方法減少了粒子濾波器中不必要的重取樣過程的次數,從而大大降低了粒子耗盡的風險。該演算法通過應用不同機器人裝備鐳射測距儀進行了多次實驗。在這些實驗中,該演算法所需的粒子數量通常比原始RBPF演算法所需的粒子數小一個數量級,證明了其魯棒性、優越性。
REFERENCES
http://blog.csdn.net/u010545732/article/details/17462941 粒子濾波(Particle filter)matlab實現
http://blog.csdn.net/heyijia0327/article/details/40899819 Particle
Filter Tutorial 粒子濾波:從推導到應用
http://ishare.iask.sina.com.cn/f/24615049.html 粒子濾波理論
