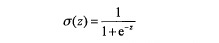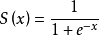《機器學習實戰》——logistic迴歸
說明:對書中程式碼錯誤部分做了修正,可運行於python3.4
基本原理:現在有一些資料點,用一條直線對這些資料進行擬合,將它們分為兩類。這條直線叫做最佳擬合直線,這個擬合過程叫做迴歸。logistic迴歸的思想是,利用一個階躍函式(在某一點突然由0變1),實現分類器。Sigmoid函式近似於階躍函式:
現在將每個特徵乘以一個迴歸係數,再全部相加,總和帶入函式作為輸入自變數z,進而得到一個0-1之間輸出,四捨五入之後劃分為0和1兩類。這就是分類器的思想。它的代價函式為:

關鍵詞:資料點,直線,最佳擬合,Sigmoid階躍函式,迴歸係數
演算法實施:
1.資料。假設文字有m行3列,第一列是第零維繫數w=1.0,第2、3列是特徵x1,x2——loadDataSet()
2. sigmoid函式。套用公式——sigmoid(inX)
3. 梯度演算法。梯度上升演算法,求出最佳的w引數(矩陣),每次計算梯度需要所有資料點資訊.——gradAscent(dataMatIn, classLabels)
隨機梯度上升演算法,改進之後,每次計算梯度只需要帶入一個數據點資訊——stocGradAscent0(dataMatrix,
classLabels)
改進後的隨機梯度上升演算法——stocGradAscent1(dataMatrix,
classLabels,numIter = 150)
4. 計算單詞出現的條件概率。首先計算侮辱性句子在所有句子中的比例
測試:為了避免各個單詞條件概率聯乘中出現的零概率,所有詞出現次數(分子)初始化為1,該類別總詞數(分母)出現次數初始化為2.0——trainNB0(trainMatrix, trainCategory)
5. 畫出資料散點圖和擬合直線。——plotBestFit(weights)
演算法程式碼:
# coding utf-8
from numpy import *
def loadDataSet():
#####資料匯入#######
dataMat = [] # 資料矩陣(第一列是w=1.0,第2、3列是特徵)
labelMat = [] # 標籤矩陣(標識每行資料的類別)
# fd = open('testSet.txt') # 格式:2.2 3.0 1
myArr = [[-3.5, -3, 0],[-2.3, 0, 0],
[-1.0, -0.1, 0],[-1.3, -1.0, 0],
[-2.5, 5, 0],[-3.5, 7, 1],
[-1.5, 16, 1],[1, 10, 1],
[1, 5, 1],[1, 3, 0]]
# for item in fd.readlines():
for itemArr in myArr:
# itemArr = item.strip().split()
dataMat.append([1.0, float(itemArr[0]), float(itemArr[1])])
labelMat.append(int(itemArr[2]))
return dataMat, labelMat
def sigmoid(inX):
#####計算sigmoid函式(即logistic函式)#####
return 1.0/(1+exp(-inX))
def gradAscent(dataMatIn, classLabels):
#####梯度上升演算法,求出最佳的w引數矩陣#######
dataMatrix = mat(dataMatIn) # dataMatIn格式:(1.0,第一特徵值,第二特徵值)
labelMat = mat(classLabels).transpose() # 標籤向量轉置為列矩陣
m,n = shape(dataMatrix) # n*3
alpha = 0.001 # 梯度表示移動方向,而alpha表示移動量的大小(步長)
maxCycles = 500 # 最多移動的步數(步數越多越精確)
weights = ones((n,1))
for k in range(maxCycles):
h = sigmoid(dataMatrix*weights)
error = (labelMat - h)
weights = weights + alpha * dataMatrix.transpose() * error
return weights
def stocGradAscent0(dataMatrix, classLabels):
#####隨機梯度上升演算法,一次僅用一個樣本點來更新迴歸係數#######
dataMatrix = mat(dataMatrix) # dataMatIn格式:(1.0,第一特徵值,第二特徵值)
labelMat = mat(classLabels).transpose() # 標籤向量轉置為列矩陣
m,n = shape(dataMatrix)
alpha = 0.001
weights = ones((n,1))
for i in range(m):
h = sigmoid(sum(dataMatrix[i]*weights))
error = classLabels[i] - h
weights = weights + alpha*error*dataMatrix[i].transpose()
return weights
def stocGradAscent1(dataMatrix, classLabels,numIter = 150):
#####隨機梯度上升演算法,一次僅用一個樣本點來更新迴歸係數#######
dataMatrix = mat(dataMatrix) # dataMatIn格式:(1.0,第一特徵值,第二特徵值)
labelMat = mat(classLabels).transpose() # 標籤向量轉置為列矩陣
m,n = shape(dataMatrix)
alpha = 0.001
weights = ones((n,1))
for j in range(numIter):
dataIndex = range(m)
for i in range(m):
alpha = 4/(1.0 + j +i)+0.01
randIndex = int(random.uniform(0,len(dataIndex)))
h = sigmoid(sum(dataMatrix[randIndex]*weights))
error = classLabels[randIndex] - h
weights = weights + alpha*error*dataMatrix[randIndex].transpose()
return weights
def plotBestFit(weights):
#####畫出最佳擬合直線#######
import matplotlib.pyplot as plt
dataArr = array(dataMat) # 矩陣轉化為陣列
n = shape(dataArr)[0]
xcord1 = []; ycord1 = []
xcord2 = []; ycord2 = []
for i in range(n):
if int(labelMat[i]) == 1:
xcord1.append(dataArr[i,1]); ycord1.append(dataArr[i,2])
else:
xcord2.append(dataArr[i,1]); ycord2.append(dataArr[i,2])
fig = plt.figure()
# 在子圖中畫出樣本點
ax = fig.add_subplot(111)
ax.scatter(xcord1, ycord1, s=30, c='red',marker='s')
ax.scatter(xcord2, ycord2, s=30, c='green')
# 畫出擬合直線
x = arange(-3.0,3.0,0.1)
y = array((-weights[0]-weights[1]*x)/weights[2])[0]
ax.plot(x,y)
plt.xlabel('X1');plt.ylabel('X2')
plt.show()
dataMat, labelMat = loadDataSet()
# weights = gradAscent(dataMat, labelMat) # 梯度上升演算法。此時weights型別為矩陣
# weights = stocGradAscent0(dataMat, labelMat) # 隨機梯度上升演算法。此時weights型別為矩陣
weights = stocGradAscent1(dataMat, labelMat) # 改進的隨機梯度上升演算法。此時weights型別為矩陣
plotBestFit(weights)
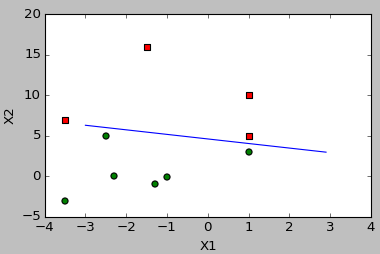
結果:
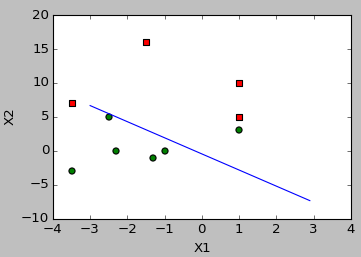
1.梯度上升演算法
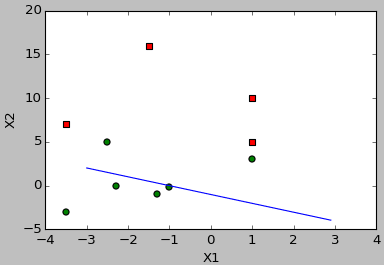
2.隨機梯度上升演算法
3.改進的隨機梯度上升演算法