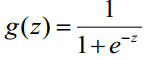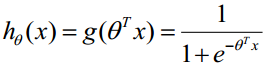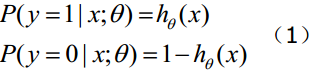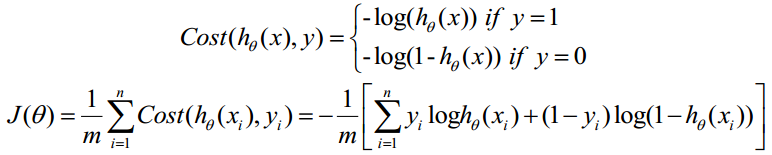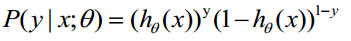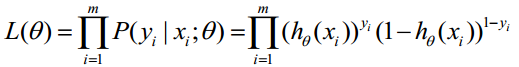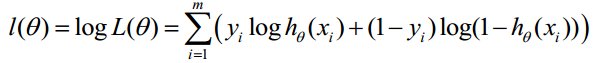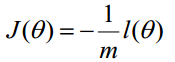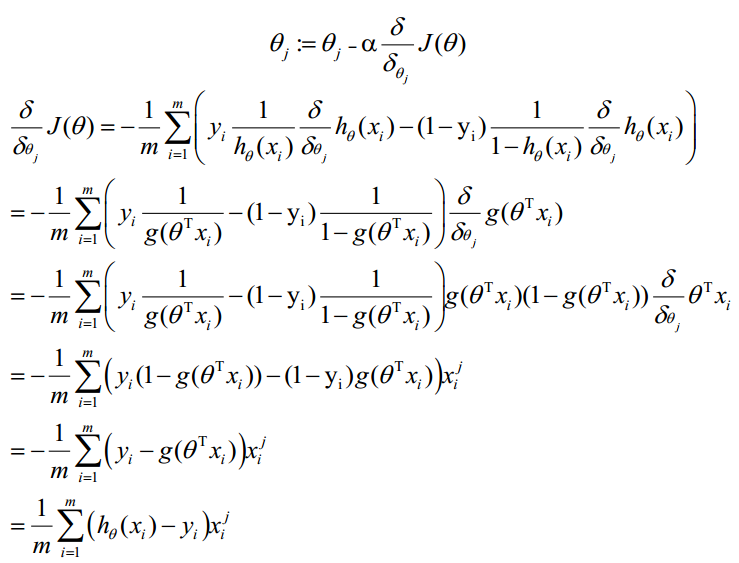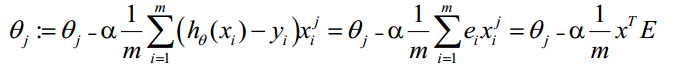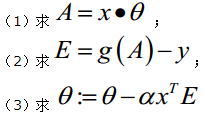1. 概念

邏輯迴歸就是這樣的一個過程：面對或者分類問題，建立代價函式然後通優化方法迭代求解出最優的模型引數，然後測試驗證我們這個好壞。

2. Regression常規步驟

Ÿ尋找h函式（即預測函式）；

Ÿ構造 J函式（損失）；函式（損失）；

Ÿ想辦法使得 J函式最小並求得迴歸參（θ）

• 構造預測函式h：

logistic迴歸雖然名字裡帶“迴歸”，但是它實際上是一種分類方法，主要用於兩分類問題（即輸出只有兩種，分別代表兩個類別），所以利用了Logistic函式（或稱為Sigmoid函式），函式形式為：

對於線性邊界的情況，邊界形式如下：

構造預測函式為：

函式h（x）的值有特殊的含義，它表示結果取1

• 構造損失函式J:

Cost函式和J函式如下，它們是基於最大似然估計推導得到的。

下面詳細說明推導的過程：

（1）式綜合起來可以寫成

取似然函式為：

對數似然函式為：

最大似然估計就是求使l(θ)取最大值時的θ，其實這裡可以使用梯度上升法求解，求得的θ就是要求的最佳引數。（最大似然概率，就是在已知觀測的資料的前提下，找到使得似然概率最大的引數值。）

但是，在Andrew Ng的課程中將J(θ)取為下式，即：

因為乘了一個負的係數-1/m，所以取J()最小值時的θ為要求的最佳引數。

• 梯度下降法求的最小值

θ更新過程：

θ更新過程可以寫成：

• 向量化 Vectorization

Vectorization是使用矩陣計算來代替 for迴圈，以簡化計算過程提高效率。如上式，Σ(...)是一個求和的過程，顯然需要一個for語句迴圈m次，所以根本沒有完全的實現vectorization。

下面介紹向量化的過程：

約定訓練資料的矩陣形式如下，x的每一行為一條訓練樣本，而每一列為不同的特稱取值：

g(A)的引數A為一列向量，所以實現g函式時要支援列向量作為引數，並返回列向量。由上式可知h(x)-y，可由g(A)-y一次計算求得。θ更新過程可以改為：

綜上所述，Vectorization後θ更新的步驟如下：

3. python演算法包實現邏輯迴歸

• 使用的演算法包：

numpy: Python的語言擴充套件，定義了數字的陣列和矩陣

pandas: 直接處理和操作資料的主要package

statsmodels: 統計和計量經濟學的package，包含了用於引數評估和統計測試的實用工具

pylab: 用於生成統計圖

• 邏輯迴歸的例項<http://www.powerxing.com/logistic-regression-in-python/>

辨別不同的因素對研究生錄取的影響。資料集中的前三列可作為預測變數(predictorvariables)：gpa/gre分數/rank表示本科生母校的聲望。第四列admit則是二分類目標變數(binary targetvariable)，它表明考生最終是否被錄用。

• 載入資料

使用 pandas.read_csv載入資料，這樣我們就有了可用於探索資料的DataFrame

import pandas as pd
import statsmodels.apias sm
import pylab as pl
import numpy as np
 
# 載入資料
# 備用地址: http://cdn.powerxing.com/files/lr-binary.csv
df = pd.read_csv("http://www.ats.ucla.edu/stat/data/binary.csv")
 
# 瀏覽資料集
print df.head()
# admit gre gpa rank
# 0 0 380 3.61 3
# 1 1 660 3.67 3
# 2 1 800 4.00 1
# 3 1 640 3.19 4
# 4 0 520 2.93 4
 
#重新命名'rank'列，因為dataframe中有個方法名也為'rank'
df.columns = ["admit", "gre", "gpa", "prestige"]
print df.columns
# array([admit, gre, gpa,prestige], dtype=object)

• 統計摘要(Summary Statistics) 以及 檢視資料

現在我們就將需要的資料正確載入到Python中了，現在來看下資料。我們可以使用pandas的函式describe來給出資料的摘要–describe與R語言中的summay類似。這裡也有一個用於計算標準差的函式std，但在describe中已包括了計算標準差。我特別喜歡pandas的pivot_table/crosstab聚合功能。crosstab可方便的實現多維頻率表(frequencytables)(有點像R語言中的table)。你可以用它來檢視不同資料所佔的比例。

# summarize the data
print df.describe()
# admit gre gpa prestige
# count 400.000000 400.000000400.000000 400.00000
# mean 0.317500 587.7000003.389900 2.48500
# std 0.466087 115.5165360.380567 0.94446
# min 0.000000 220.0000002.260000 1.00000
# 25% 0.000000 520.0000003.130000 2.00000
# 50% 0.000000 580.0000003.395000 2.00000
# 75% 1.000000 660.0000003.670000 3.00000
# max 1.000000 800.0000004.000000 4.00000
 
# 檢視每一列的標準差
print df.std()
# admit 0.466087
# gre 115.516536
# gpa 0.380567
# prestige 0.944460
 
# 頻率表，表示prestige與admin的值相應的數量關係
print pd.crosstab(df['admit'], df['prestige'],rownames=['admit'])
# prestige 1 2 3 4
# admit
# 0 28 97 93 55
# 1 33 54 28 12
 
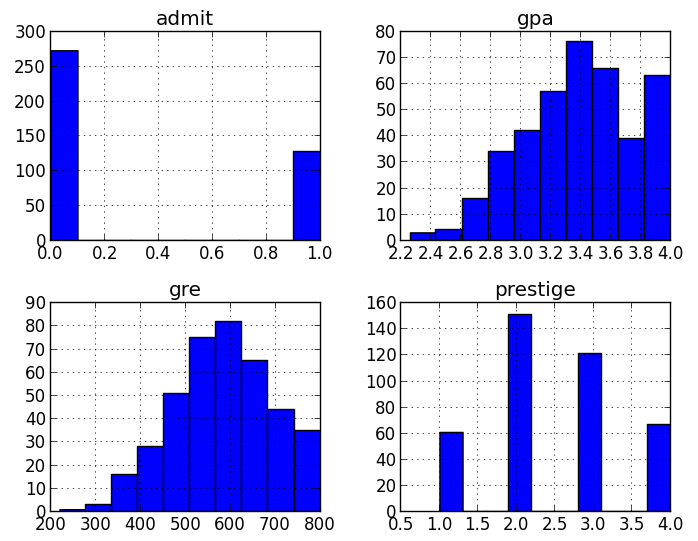
# plot all of the columns
df.hist()
pl.show()

• 虛擬變數(dummy variables)

虛擬變數，也叫啞變數，可用來表示分類變數、非數量因素可能產生的影響。在計量經濟學模型，需要經常考慮屬性因素的影響。例如，職業、文化程度、季節等屬性因素往往很難直接度量它們的大小。只能給出它們的“Yes—D=1”或”No—D=0”，或者它們的程度或等級。為了反映屬性因素和提高模型的精度，必須將屬性因素“量化”。通過構造0-1型的人工變數來量化屬性因素。

pandas提供了一系列分類變數的控制。我們可以用get_dummies來將”prestige”一列虛擬化。

get_dummies為每個指定的列建立了新的帶二分類預測變數的DataFrame，在本例中，prestige有四個級別：1，2，3以及4（1代表最有聲望），prestige作為分類變數更加合適。當呼叫get_dummies時，會產生四列的dataframe，每一列表示四個級別中的一個。

# 將prestige設為虛擬變數
dummy_ranks = pd.get_dummies(df['prestige'],prefix='prestige')
print dummy_ranks.head()
# prestige_1 prestige_2prestige_3 prestige_4
# 0 0 0 1 0
# 1 0 0 1 0
# 2 1 0 0 0
# 3 0 0 0 1
# 4 0 0 0 1
 
# 為邏輯迴歸建立所需的data frame
#除admit、gre、gpa外，加入了上面常見的虛擬變數（注意，引入的虛擬變數列數應為虛擬變數總列數減1，減去的1列作為基準）
cols_to_keep = ['admit', 'gre', 'gpa']
data = df[cols_to_keep].join(dummy_ranks.ix[:, 'prestige_2':])
print data.head()
# admit gre gpa prestige_2prestige_3 prestige_4
# 0 0 380 3.61 0 1 0
# 1 1 660 3.67 0 1 0
# 2 1 800 4.00 0 0 0
# 3 1 640 3.19 0 0 1
# 4 0 520 2.93 0 0 1
 
# 需要自行新增邏輯迴歸所需的intercept變數
data['intercept'] = 1.0

這樣，資料原本的prestige屬性就被prestige_x代替了，例如原本的數值為2，則prestige_2為1，prestige_1、prestige_3、prestige_4都為0。將新的虛擬變數加入到了原始的資料集中後，就不再需要原來的prestige列了。在此要強調一點，生成m個虛擬變數後，只要引入m-1個虛擬變數到資料集中，未引入的一個是作為基準對比的。最後，還需加上常數intercept，statemodels實現的邏輯迴歸需要顯式指定。

• 執行邏輯迴歸

實際上完成邏輯迴歸是相當簡單的，首先指定要預測變數的列，接著指定模型用於做預測的列，剩下的就由演算法包去完成了。

本例中要預測的是admin列，使用到gre、gpa和虛擬變數prestige_2、prestige_3、prestige_4。prestige_1作為基準，所以排除掉，以防止多元共線性(multicollinearity)和引入分類變數的所有虛擬變數值所導致的陷阱(dummy variable trap)。

# 指定作為訓練變數的列，不含目標列`admit`
train_cols = data.columns[1:]
# Index([gre, gpa, prestige_2,prestige_3, prestige_4], dtype=object)
 
logit = sm.Logit(data['admit'], data[train_cols])
 
# 擬合模型
result = logit.fit()

在這裡是使用了statesmodels的Logit函式，更多的模型細節可以查閱statesmodels的文件

• 使用訓練模型預測資料

通過上述步驟，我們就得到了訓練後的模型。基於這個模型，我們就可以用來預測資料。

# 構建預測集
# 與訓練集相似，一般也是通過 pd.read_csv() 讀入
# 在這邊為方便，我們將訓練集拷貝一份作為預測集（不包括 admin 列）
import copy
combos = copy.deepcopy(data)
 
# 資料中的列要跟預測時用到的列一致
predict_cols = combos.columns[1:]
 
# 預測集也要新增intercept變數
combos['intercept'] = 1.0
 
# 進行預測，並將預測評分存入 predict 列中
combos['predict'] = result.predict(combos[predict_cols])
 
# 預測完成後，predict 的值是介於 [0, 1]間的概率值
# 我們可以根據需要，提取預測結果
# 例如，假定 predict > 0.5，則表示會被錄取
# 在這邊我們檢驗一下上述選取結果的精確度
total = 0
hit = 0
for value in combos.values:
# 預測分數 predict, 是資料中的最後一列
predict = value[-1]
# 實際錄取結果
admit = int(value[0])
 
# 假定預測概率大於0.5則表示預測被錄取
if predict > 0.5:
total += 1
# 表示預測命中
if admit == 1:
hit += 1
 
# 輸出結果
print 'Total: %d, Hit: %d, Precision: %.2f' % (total, hit, 100.0*hit/total)
# Total: 49, Hit: 30, Precision:61.22
 

• 結果解釋

statesmodels提供了結果的摘要，如果你使用過R語言，你會發現結果的輸出與之相似

# 檢視資料的要點
print result.summary()
Logit Regression Results
==============================================================================
Dep. Variable: admit No. Observations: 400
Model: Logit Df Residuals: 394
Method: MLE Df Model: 5
Date: Sun, 03 Mar 2013 Pseudo R-squ.: 0.08292
Time: 12:34:59 Log-Likelihood: -229.26
converged: True LL-Null: -249.99
LLR p-value: 7.578e-08
==============================================================================
coef std err z P>|z| [95.0% Conf. Int.]
------------------------------------------------------------------------------
gre 0.0023 0.001 2.070 0.038 0.000 0.004
gpa 0.8040 0.332 2.423 0.015 0.154 1.454
prestige_2 -0.6754 0.316 -2.134 0.033 -1.296 -0.055
prestige_3 -1.3402 0.345 -3.881 0.000 -2.017 -0.663
prestige_4 -1.5515 0.418 -3.713 0.000 -2.370 -0.733
intercept -3.9900 1.140 -3.500 0.000 -6.224 -1.756
==============================================================================
 

你可以看到模型的係數，係數擬合的效果，以及總的擬合質量，以及一些統計度量。[待補充:模型結果主要引數的含義]當然你也可以只觀察結果的某部分，如置信區間(confidence interval)可以看出模型係數的健壯性。

# 檢視每個係數的置信區間
printresult.conf_int()
# 0 1
# gre 0.000120 0.004409
# gpa 0.153684 1.454391
# prestige_2 -1.295751 -0.055135
# prestige_3 -2.016992 -0.663416
# prestige_4 -2.370399 -0.732529
# intercept -6.224242 -1.755716

在這個例子中，我們可以肯定被錄取的可能性與應試者畢業學校的聲望存在著逆相關的關係。

換句話說，高排名學校（prestige_1==True）的湘鄂生唄錄取的概率比低排名學校（prestige_4==True）要高。

• 相對危險度（odds ratio）

使用每個變數係數的指數來生成odds ratio，可知變數每單位的增加、減少對錄取機率的影響。例如，如果學校的聲望為2，則我們可以期待被錄取的機率減少大概50%。UCLA上有一個對oddsratio更為深入的解釋:在邏輯迴歸中如何解釋oddsratios?。

# 輸出 odds ratio
printnp.exp(result.params)
# gre 1.002267
# gpa 2.234545
# prestige_2 0.508931
# prestige_3 0.261792
# prestige_4 0.211938
# intercept 0.018500

我們也可以使用置信區間來計算係數的影響，來更好地估計一個變數影響錄取率的不確定性。

# odds ratios and 95% CI
params = result.params
conf = result.conf_int()
conf['OR'] = params
conf.columns = ['2.5%', '97.5%', 'OR']
print np.exp(conf)
# 2.5% 97.5% OR
# gre 1.000120 1.004418 1.002267
# gpa 1.166122 4.281877 2.234545
# prestige_2 0.273692 0.9463580.508931
# prestige_3 0.133055 0.5150890.261792
# prestige_4 0.093443 0.4806920.211938
# intercept 0.001981 0.1727830.018500

4. 小結

邏輯迴歸是用於分類的優秀演算法，儘管有一些更加性感的，或是黑盒分類器演算法，如SVM和隨機森林（RandomForest）在一些情況下效能更好，但深入瞭解你正在使用的模型是很有價值的。很多時候你可以使用隨機森林來篩選模型的特徵，並基於篩選出的最佳的特徵，使用邏輯迴歸來重建模型。