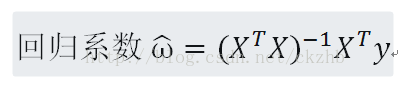環境：Adaconda3  python3.6

注：本程式相比原書中的程式區別，主要區別在於函式驗證和繪圖部分。

一、一般線性迴歸（最小二乘法OLS）

迴歸係數求解公式：

說明：X矩陣中每一行是一個樣本，y是列向量。只有逆矩陣存在的時候使用，必須在程式碼中進行判斷。

from numpy import *
import matplotlib.pyplot as plt
# 自適應資料載入函式
# 不必指定特徵數目,
def loadDataSet(fileName):     #general function to parse tab -delimited floats
    numFeat = len(open(fileName).readline().split('\t'))-1   #get number of fields
    dataMat = [];labelMat = []
    with open(fileName) as fr:
        for line in fr.readlines():
            lineArr = []
            curLine = line.strip().split('\t')
            for i in range(numFeat):
                lineArr.append(float(curLine[i]))
            dataMat.append(lineArr)
            labelMat.append(float(curLine[-1]))
    return dataMat,labelMat       # 返回列表
# xMat:每一行是一個樣本
def standRegres(xArr,yArr):
    xMat = mat(xArr)
    yMat = mat(yArr).T
    xTx = xMat.T * xMat
    if linalg.det(xTx)==0.0:    #判斷是否可逆
        print('This matrix is singular,cannot do inverse')
        return
    ws = xTx.I * (xMat.T * yMat)
    return ws         #返回矩陣
x,y = loadDataSet('ex0.txt')  # 檔案中第一列全為1
def test(x,y):
    # 繪製散點圖
    xMat = array(x)
    yMat = array(y)
    ws1 = standRegres(x,y)
    fig = plt.figure(1)
    ax = fig.add_subplot(111)
    ax.scatter(xMat[:,1],yMat.transpose())
    # 繪製擬合曲線
    # 排序後在畫擬合直線??
    y_fit = dot(xMat,ws1)  # 矩陣乘法
    # 計算相關序列
    print(corrcoef(y_fit.transpose(),yMat))
    ax.plot(xMat[:,1],y_fit,c='r')
    plt.show()
#print(test(x,y))
 

線性迴歸的一個問題是欠擬合，考慮加入一些偏差，降低預測的均方誤差。

LWLR方法對待預測的每個點賦予一定的權重，在這樣的一個子集上基於最小均方差來進行普通的迴歸。

因此，會增加計算量，它對每個點做預測時都必須使用整個資料集。

權重常採用“核”函式的方式進行加權，本程式使用高斯核。

說明：等號右邊的W表示權重係數。

# 資料載入函式同上
# 區域性線性加權迴歸
# k:高斯核引數
def lwlr(testPoint,xArr,yArr,k=1.0):
    xMat = mat(xArr)
    yMat = mat(yArr).T
    m = shape(xMat)[0]
    weights = mat(eye(m))
    for j in range(m):
        diffMat = testPoint - xMat[j,:]
        weights[j,j] = exp(diffMat*diffMat.T/(-2.0*k**2))
    xTx = xMat.T * (weights * xMat)
    if linalg.det(xTx) == 0.0:
        print('This matrix is singular,cannot do inverse')
        return
    ws = xTx.I * (xMat.T * (weights * yMat))
    return testPoint*ws
#print(lwlr(x[0],x,y,1.0))
def lwlrTest(testArr,xArr,yArr,k=1.0):
    #獲取所有資料的估計值
    xMat = mat(xArr)
    yMat = mat(yArr)
    m,n = shape(xMat)
    y_fit = zeros(m)
    for i in range(m):
        y_fit[i] = lwlr(testArr[i],xArr,yArr,k)
    # 繪製散點圖
    fig = plt.figure(1)
    ax = fig.add_subplot(111)
    ax.scatter(xMat[:,1].flatten().getA(),yMat.getA())    #必須是陣列的形式
    # 繪製擬合曲線
    # 排序後再畫擬合直線
    srtIndex = xMat[:,1].argsort(axis=0)
    xSort = xMat[srtIndex][:,0,:]
    ySort = y_fit[srtIndex]
    #ax.plot(xMat[:,1],y_fit,c='r')  #未排序，曲線明顯出錯
    ax.plot(xSort[:,1],ySort,c='r')
    plt.show()
    return y_fit
print(lwlrTest(x,x,y,0.03))
 

1、繪製圖形時報錯：Masked arrays must be 1-D

解決：scatter()中引數必須是1-D的array，但plot()總引數可以是矩陣。

ax.scatter(xMat[:,1].flatten().getA(),yMat.getA())    #必須是陣列的形式

解釋：http://blog.csdn.net/qq_18433441/article/details/54916991

numpy的flatten()可以將二維矩陣變為一維的矩陣，但此時依然是矩陣型別。

from numpy import *
a=[[1,2,3],[4,5,6]]
mat1 = mat(a)
mat2 = mat1.flatten()  #依然是matrix型別
mat3 = mat2.getA()    # array型別
print(a)
print(mat1)
print(mat2,type(mat2))
print(mat3,type(mat3))
 

情形一：原物件整體改變

結果：引用後物件和copy()後物件不隨原物件而改變

from numpy import *
b1=array([1,2,3,4,5,6])
b2=b1
b3=b1.copy()
b1=b1*2
print(b1)
print(b2)
print(b3)

[ 2  4  6  8 10 12]
[1 2 3 4 5 6]
[1 2 3 4 5 6]

結果：引用物件隨原物件改變，copy()後的物件不變

from numpy import *
b1=array([1,2,3,4,5,6])
b2=b1
b3=b1.copy()
b1[0]=100
print(b1)
print(b2)
print(b3)

[100   2   3   4   5   6]
[100   2   3   4   5   6]
[1 2 3 4 5 6]

結果：子物件變化時，引用後物件和copy()後物件均隨原物件而改變。但是，非子物件變化的結果同上。

（1）非子物件改變

b1=[1,2,[3,4]]
b2=b1
b3=b1.copy()
b1[0]=100
print(b1)
print(b2)
print(b3)

[100, 2, [3, 4]]
[100, 2, [3, 4]]
[1, 2, [3, 4]]

b1=[1,2,[3,4]]
b2=b1
b3=b1.copy()
#b1[0]=100
b1[2][0] = 100
print(b1)
print(b2)
print(b3)

[1, 2, [100, 4]]
[1, 2, [100, 4]]
[1, 2, [100, 4]]

比如array([1,2,[3,4]])  錯誤

情形四：完全複製

copy庫函式之deepcopy()，list無deepcopy屬性，因此list.deepcopy()錯誤！

import copy
b1=[1,2,[3,4]]
b2=b1
b3=b1.copy()
b4=copy.deepcopy(b1)
#b1[0]=100
b1[2][0] = 100
print(b1)
print(b2)
print(b3)
print(b4)

[1, 2, [100, 4]]
[1, 2, [100, 4]]
[1, 2, [100, 4]]
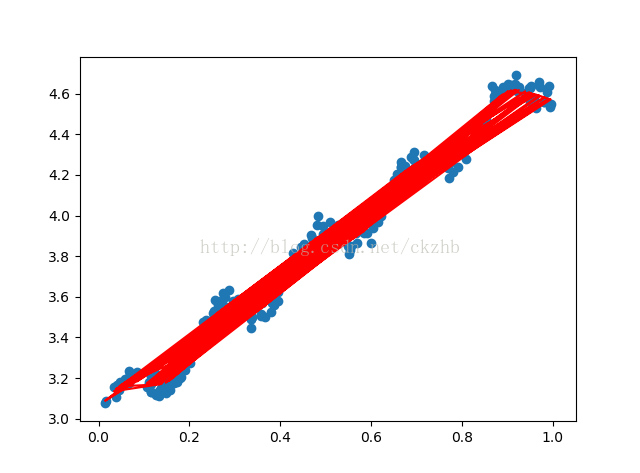
[1, 2, [3, 4]]

3、問題：擬合曲線繪製前必須先對資料線進行排序，否則易出錯！！！

未排序繪製的擬合曲線：

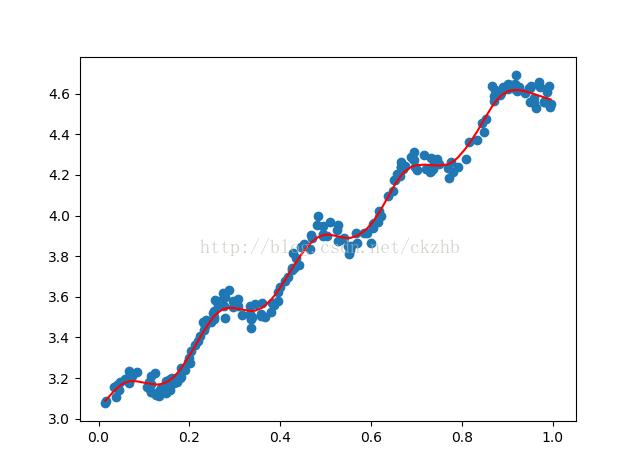
排序後再繪製擬合曲線：