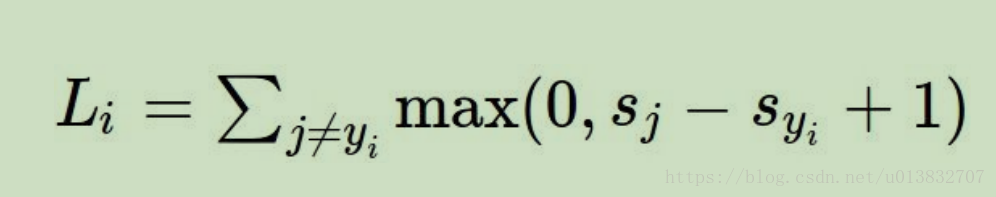斯坦福深度學習課程cs231n assignment1作業筆記二:SVM實現相關
阿新 • • 發佈:2019-02-04
前言
本次作業需要完成:
- 實現SVM損失函式,並且是完全向量化的
- 實現相關的梯度計算,也是向量化的
- 使用數值梯度驗證梯度是否正確
- 使用驗證集來選擇一組好的學習率以及正則化係數
- 使用SGD方法優化loss
- 視覺化最終的權重
程式碼實現
使用for迴圈計算SVM的loss以及grad
其中W為權重矩陣,形狀為(D,C);X為測試資料,形狀為(N,D);y為X對應的標籤值,形狀為(N,);reg為正則化係數。
函式需要返回float型的loss以及W對應的梯度矩陣
svm的損失函式如下:
其中si是f(w,x)的計算結果S(N,)的第i項。表示樣本屬於第i類的概率,syi表示樣本被分為正確類別的概率。
實現svm_loss_naive(W, X, y, reg)函式
def svm_loss_naive(W, X, y, reg):
"""
Structured SVM loss function, naive implementation (with loops).
Inputs have dimension D, there are C classes, and we operate on minibatches
of N examples.
Inputs:
- W: A numpy array of shape (D, C) containing weights.
- X: A numpy array of shape (N, D) containing a minibatch of data.
- y: A numpy array of shape (N,) containing training labels; y[i] = c means
that X[i] has label c, where 0 <= c < C.
- reg: (float) regularization strength
Returns a tuple of:
- loss as single float
- gradient with respect to weights W; an array of same shape as W
""" 實現svm_loss_vectorized(W, X, y, reg)函式
def svm_loss_vectorized(W, X, y, reg):
"""
Structured SVM loss function, vectorized implementation.
Inputs and outputs are the same as svm_loss_naive.
"""
loss = 0.0
dW = np.zeros(W.shape) # initialize the gradient as zero
#############################################################################
# TODO: #
# Implement a vectorized version of the structured SVM loss, storing the #
# result in loss. #
#############################################################################
num_train = X.shape[0]
num_classes = W.shape[1]
scores = X.dot(W)
correct_class_scores = scores[np.arange(num_train), y]
margins = np.maximum(0, scores - correct_class_scores[:, np.newaxis] + 1.0)
margins[np.arange(num_train), y] = 0
loss = np.sum(margins)
loss /= num_train
loss += reg * np.sum(W * W)
#############################################################################
# END OF YOUR CODE #
#############################################################################
#############################################################################
# TODO: #
# Implement a vectorized version of the gradient for the structured SVM #
# loss, storing the result in dW. #
# #
# Hint: Instead of computing the gradient from scratch, it may be easier #
# to reuse some of the intermediate values that you used to compute the #
# loss. #
#############################################################################
D = W.shape[0]
dm_s = np.zeros_like(margins)
dm_s[margins > 0] = 1
num_pos = np.sum(margins > 0, axis=1)
dm_s[np.arange(num_train), y] = -num_pos
dW = X.T.dot(dm_s)
dW /= num_train
dW += W*2
#############################################################################
# END OF YOUR CODE #
#############################################################################
return loss, dW
結果
numerical: 1.680214 analytic: 1.679971, relative error: 7.230767e-05
numerical: -11.835214 analytic: -11.835290, relative error: 3.186856e-06
numerical: 31.223996 analytic: 31.224021, relative error: 3.971612e-07
numerical: -11.983471 analytic: -11.983169, relative error: 1.261847e-05
numerical: 14.276020 analytic: 14.275969, relative error: 1.817105e-06
numerical: 60.570112 analytic: 60.570076, relative error: 3.005679e-07
numerical: -21.435424 analytic: -21.435447, relative error: 5.177246e-07
numerical: 10.956106 analytic: 10.956302, relative error: 8.935366e-06
numerical: 15.374184 analytic: 15.374405, relative error: 7.184253e-06
numerical: 18.606596 analytic: 18.606262, relative error: 8.968162e-06
numerical: 6.584964 analytic: 6.576627, relative error: 6.334218e-04
numerical: -53.592687 analytic: -53.587162, relative error: 5.154812e-05
numerical: -37.440261 analytic: -37.452605, relative error: 1.648300e-04
numerical: -4.948189 analytic: -4.938414, relative error: 9.887377e-04
numerical: -28.108544 analytic: -28.111811, relative error: 5.811183e-05
numerical: 19.087159 analytic: 19.079373, relative error: 2.040010e-04
numerical: 39.119884 analytic: 39.115284, relative error: 5.880564e-05
numerical: -11.900470 analytic: -11.914449, relative error: 5.870076e-04
numerical: -17.774522 analytic: -17.779592, relative error: 1.426094e-04
numerical: -10.194233 analytic: -10.194915, relative error: 3.343300e-05
實現SGD
在實現了loss和gradient計算之後,實現SGD是很簡單的事情,所以就不貼程式碼了