如果以面向物件(OOP)的方式進行BP神經網路系統的設計與實踐的話，因為權值的初始化以及類的構造都只進行一次（而且發生在整個流程的開始階段），所以自然地將權值（全部層layer之間的全部權值）初始化的過程放在類的構函式中，而權值的初始化，一種trivial常用的初始化方法為，對各個權值使用均值為0方差為1的正態分佈（也即np.random.randn(shape)）進行初始化，也即：

class Network(object):
    # topology：表示神經網路拓撲結構，用list或者tuple來實現，
    # 比如[784, 30, 10]，表示784個神經元的輸入層，30個neuron的隱層，以及十個neuron的輸出層
 

    def __init__(self, topology):
        self.topology = topology
        self.num_layers = len(topology)
        self.biases = [np.random.randn(y, 1) for y in topology[1:]]
        self.weights = [np.random.randn(y, x) for x, y in zip(self.weights[:-1], self.weights[1:])]

我們不妨以一個簡單的具體例子，分析這種初始化方法可能存在的缺陷，如下圖所示：

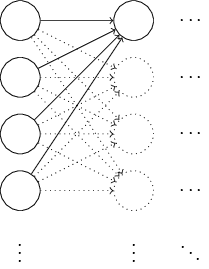
為了簡化問題，我們只以最左一層向中間一層的第一個神經元（neuron）進行前向（forward）傳遞為例進行分析，假設一個輸入樣本（特徵向量，x，維度為1000），一半為1，一半為0（這樣的假設很特殊，但也很能說明問題），根據前向傳遞公式，z=∑jwjxj+b，z即為輸入層向中間隱層第一個神經元的輸入。因為輸入的一半為0的緣故，再根據前文以及程式碼也即權重和偏置初始化為獨立同分布的標準高斯隨機變數，z為501（500個權值+1個偏置）個標準正太隨機變數的和，由獨立隨機變數和的方差等於方差的和可知，因此z的分佈服從0均值，標準差為501−−−√≈22.4，標準差從1升高到22.4，由高斯密度函式f(x)

=12π√σexp(−(x−μ)2σ2)可知，方差越大，密度函式的分佈越扁平，也即分佈越均勻而不是集中在一段區域，其概率密度函式為（可見十分平坦）：

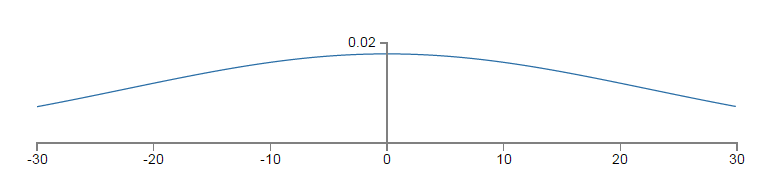
以上的平坦的概率密度函式為z的pdf（概率密度函式），因為pdf較為均勻，|z|的值就不會像N∼(0,1)那樣集中於均值附近（越遠離均值中心，密度值會迅速衰減），而會以更大的概率取更大的值。這中初始化機制可能帶來什麼樣的問題呢？|z|取值很大，也即z≫1或者z≪−1，相應的該神經元的activation值σ(z)就會接近0或者1，而我們知道，如下圖示，σ(z)越靠近0或者1其變化率越小，也即是達到一種飽和（saturate）狀態。

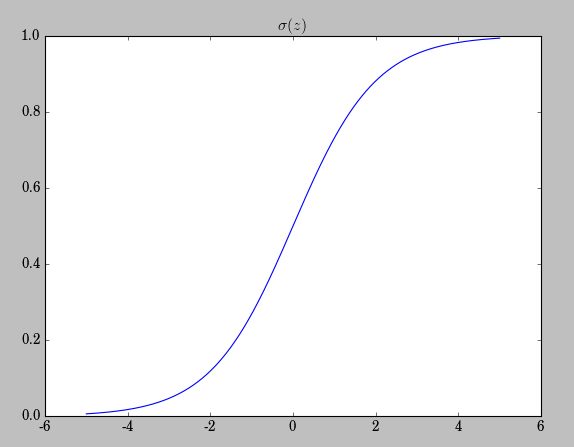
而權值更新公式為：

∂C∂wL=(aL−y)σ′(z)
也就意味著越小的σ′(z)，越小的梯度更新，同等學習率（learning rate：η）的情況下，越小的學習速率。

如何進行改進呢？假使輸入層有nin個神經元，我們可將這些神經元對應的權重初始化為0均值，標準差為1/(√nin)，這樣，高斯pdf的形式將會趨於陡峭，而不是上文的平坦，σ′(z)將以較小的概率達到飽和狀態。仍以上文的設定為基礎，我們來分析，現在z的pdf，均值為0，標準差為500/1000−−−−−−−−√≈0.707，其形式如下：

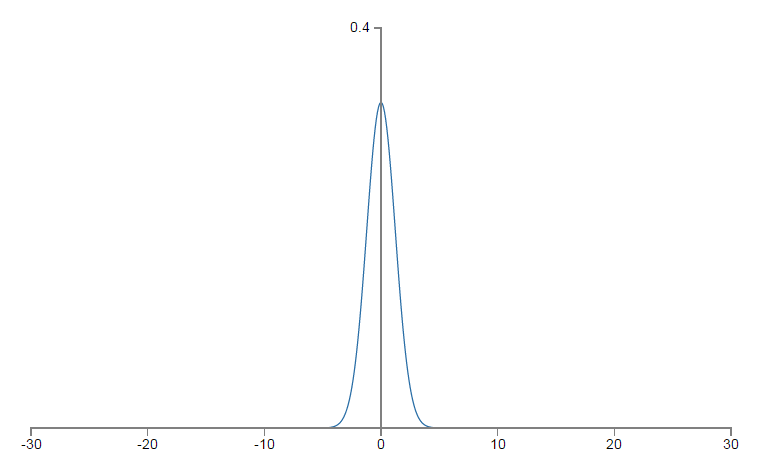
相關程式碼：

def default_weight_init(self):
    self.biases = [np.random.randn(y, 1)/y for y in self.topology[1:]] 
    self.weights = [np.random.rand(y, x)/np.sqrt(x) for x, y in zip(self.topology[:-1], self.topology[1:])]

def large_weight_init(self):
    self.biases = [np.random.randn(y, 1) for y in self.topoloy[1:]]
    self.weights = [np.random.randn(y, x)/np.sqrt(x) for x, y in zip(self.topology[:-1], self.topology[1:])]

我們看到正是這樣一種np.random.randn(y, x)向np.random.randn(y, x)/np.sqrt(x)小小的改變，卻暗含著豐富的概率論與數理統計的知識，可見無時無刻無處不體現著數學工具的強大。