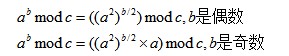快速冪取模演算法，是比較常見的演算法。分享給大家供大家參考之用。具體如下：

首先，所謂的快速冪，實際上是快速冪取模的縮寫，簡單的說，就是快速的求一個冪式的模(餘)。在程式設計過程中，經常要去求一些大數對於某個數的餘數，為了得到更快、計算範圍更大的演算法，產生了快速冪取模演算法。我們先從簡單的例子入手：求abmodc

演算法1.直接設計這個演算法：

int ans = 1;
for(int i = 1;i<=b;i++)
{
  ans = ans * a;
}
ans = ans % c;

缺點：這個演算法存在著明顯的問題，如果a和b過大，很容易就會溢位。

我們先來看看第一個改進方案：在講這個方案之前，要先看這樣一個公式：ab mod c = (a mod c)c mod c

於是不用思考的進行了改進：

演算法2.改進演算法：

int ans = 1;
a = a % c; //加上這一句
for(int i = 1;i<=b;i++)
{
  ans = ans * a;
}
ans = ans % c;

讀者應該可以想到，既然某個因子取餘之後相乘再取餘保持餘數不變，那麼新算得的ans也可以進行取餘，所以得到比較良好的改進版本。

演算法3.進一步改進演算法：

int ans = 1;
a = a % c; //加上這一句
for(int i = 1;i<=b;i++)
{
  ans = (ans * a) % c;//這裡再取了一次餘
}
ans = ans % c;
 

這個演算法在時間複雜度上沒有改進，仍為O(b)，不過已經好很多的，但是在c過大的條件下，還是很有可能超時，所以，我們推出以下的快速冪演算法。

演算法4.快速冪演算法：

快速冪演算法依賴於以下明顯的公式：

int PowerMod(int a, int b, int c)
{
  int ans = 1;
  a = a % c;
  while(b>0) {
    if(b % 2 = = 1)
    ans = (ans * a) % c;
    b = b/2;
    a = (a * a) % c;
  }
  return ans;
}

本演算法的時間複雜度為O（logb），能在幾乎所有的程式設計（競賽）過程中通過，是目前最常用的演算法之一。

相信本文所述對大家演算法設計的學習有一定的借鑑價值。

部落格已搬：洪學林部落格