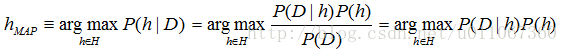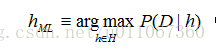在機器學習中，通常我們感興趣的是在給定訓練資料D時，確定假設空間H中的最佳假設。

所謂最佳假設，一種辦法是把它定義為在給定資料D以及H中不同假設的先驗概率的有關知識條件下的最可能（most probable）假設。

貝葉斯理論提供了計算這種可能性的一種直接的方法。更精確地講，貝葉斯法則提供了一種計算假設概率的方法，它基於假設的先驗概率、給定假設下觀察到不同資料的概率、以及觀察的資料本身。

要精確地定義貝葉斯理論，先引入一些記號。

1、P(h)來代表還沒有訓練資料前，假設h擁有的初始概率。P(h)常被稱為h的先驗概率（prior probability ），它反映了我們所擁有的關於h是一正確假設的機會的背景知識。如果沒有這一先驗知識，那麼可以簡單地將每一候選假設賦予相同的先驗概率

2、P(D)代表將要觀察的訓練資料D的先驗概率（換言之，在沒有確定某一假設成立時，D的概率）。

3、P(D|h)代表假設h成立的情形下觀察到資料D的概率。更一般地，我們使用P(x|y)代表給定y時x的概率。

在機器學習中，我們感興趣的是P(h|D)，即給定訓練資料D時h成立的概率。

P(h|D)被稱為h的後驗概率（posteriorprobability），因為它反映了在看到訓練資料D後h成立的置信度。

應注意，後驗概率P(h|D)反映了訓練資料D的影響；相反，先驗概率P(h)是獨立於D的。

貝葉斯法則是貝葉斯學習方法的基礎，因為它提供了從先驗概率P(h)以及P(D)和P(D|h)計算後驗概率P

貝葉斯公式

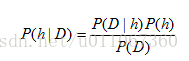
直觀可看出，P(h|D)隨著P(h)和P(D|h)的增長而增長。同時也可看出P(h|D)隨P(D)的增加而減少，這是很合理的，因為如果D獨立於h被觀察到的可能性越大，那麼D對h的支援度越小。

學習器考慮候選假設集合H並在其中尋找給定資料D時可能性最大的假設h∈H（或者存在多個這樣的假設時選擇其中之一）這樣的具有最大可能性的假設被稱為極大後驗（maximum a posteriori, MAP）假設。確定MAP假設的方法是用貝葉斯公式計算每個候選假設的後驗概率。

更精確地說當下式成立時，稱h_MAP

（在最後一步我們去掉了P(D)，因為它是不依賴於h的常量）

極大似然（maximum likelihood，ML）假設

在某些情況下，可假定H中每個假設有相同的先驗概率（即對H中任意h_i和h_j，P(h_i)=P(h_j)）。這時可把上式進一步簡化，只需考慮P(D|h)來尋找極大可能假設。P(D|h)常稱為給定h時資料D的似然度（likelihood），而使P(D|h)最大的假設被稱為極大似然（maximum likelihood，ML）假設h_ML。

為了使上面的討論與機器學習問題相聯絡，我們把資料D稱作某目標函式的訓練樣例，而把H稱為候選目標函式空間。

實際上，貝葉斯公式有著更為普遍的意義。它同樣可以很好地用於任意互斥命題的集合H，只要這些命題的概率之和為1（例如：“天空是蘭色的”和“天空不是蘭色的”）。有時將H作為包含目標函式的假設空間，而D作為訓練例集合。其他一些時候考慮將H看作一些互斥命題的集合，而D為某種資料。

貝葉斯推理的結果很大地依賴於先驗概率，要直接應用方法必須先獲取該值。