貝葉斯估計與有監督學習

如何用貝葉斯估計解決有監督學習問題？
對於有監督學習，我們的目標實際上是估計一個目標函式f : X->Y，,或目標分佈P(Y|X)，其中X是樣本的各個feature組成的多維變數，Y是樣本的實際分類結果。假設樣本X的取值為xk，那麼，根據貝葉斯定理，分類結果為yi的概率應該為：

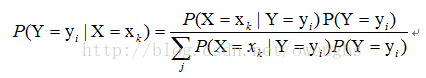
因此，要估計P(Y=yi|X=xk)，只要根據樣本，求出P(X=xk|Y=yi)的所有估計，以及P(Y=yi)的所有估計，就可以了。此後的分類過程，就是求另P(Y=yi|X=xk)最大的那個yi就可以了。那麼由此可見，利用貝葉斯估計，可以解決有監督學習的問題。

分類器的“樸素”特性

何為“樸素”？
從第3節的分析裡，我們知道，要求得P(Y=yi|X=xk)，就需要知道P(X=xk|Y=yi)的所有估計，以及P(Y=yi)的所有估計，那麼假設X為N維變數，其每一維變數都有兩種取值（如文字分類中常見的各個term出現與否對應的取值0/1），而Y也有兩種類別，那麼就需要求出2*(2^N - 1)個估計（注意，由於在給定Y為某一類別的情況下，X的各個取值的概率和為1，所以實際需要估計的值為2^N - 1）。可以想象，對於N很大的情況（文字分類時，term的可能取值是非常大的），這一估計的計算量是巨大的。那麼如何減少需要估計的量，而使得貝葉斯估計方法具有可行性呢？這裡，就引入一種假設：
假設：在給定Y=yi的條件下，X的各維變數彼此相互獨立。

那麼，在這一假設的條件下，P(X=xk|Y=yi)=P(X1=x1j1|Y=yi)P(X2=x2j2|Y=yi)…P(Xn=xnjn|Y=yi)，也就是說，此時只需要求出N個估計就可以了。因此，這一假設將貝葉斯估計的計算量從2*(2^N - 1)降為了N，使這一分類器具有了實際可行性。那麼這一假設就成為樸素特性。
貝葉斯分類器特點:
1.需要知道先驗概率先驗概率是計算後驗概率的基礎。在傳統的概率理論中，先驗概率可以由大量的重複實驗所獲得的各類樣本出現的頻率來近似獲得，其基礎是“大數定律”，這一思想稱為“頻率主義”。而在稱為“貝葉斯主義”的數理統計學派中，他們認為時間是單向的，許多事件的發生不具有可重複性，因此先驗概率只能根據對置信度的主觀判定來給出，也可以說由“信仰”來確定。
2、按照獲得的資訊對先驗概率進行修正
在沒有獲得任何資訊的時候，如果要進行分類判別，只能依據各類存在的先驗概率，將樣本劃分到先驗概率大的一類中。而在獲得了更多關於樣本特徵的資訊後，可以依照貝葉斯公式對先驗概率進行修正，得到後驗概率，提高分類決策的準確性和置信度。
3、分類決策存在錯誤率
由於貝葉斯分類是在樣本取得某特徵值時對它屬於各類的概率進行推測，並無法獲得樣本真實的類別歸屬情況，所以分類決策一定存在錯誤率，即使錯誤率很低，分類錯誤的情況也可能發生。
引數的估計
只要知道先驗概率和獨立概率分佈，就可以設計出一個貝葉斯分
類器。先驗概率不是一個分佈函式，僅僅是一個值，它表達了樣本空間中各個類的樣本所佔數量的比例。依據大數定理，當訓練集中樣本數量足夠多且來自於樣本空間的隨機選取時，可以以訓練集中各類樣本所佔的比例來估計。

極大似然估計和最大後驗概率

極大似然估計法應用於樸素貝葉斯分類器的求解過程。
上面說了，P(X=xk|Y=yi)的求解，可以轉化為對P(X1=x1j1|Y=yi)、P(X2=x2j2|Y=yi)、… P(Xn=xnjn|Y=yi)的求解，那麼如何利用極大似然估計法求這些值呢？
首選我們需要理解什麼是極大似然估計，實際上，在我們的概率論課本里，關於極大似然估計的講解，都是在解決無監督學習問題，而看完本節內容後，你應該明白，在樸素特性下，用極大似然估計解決有監督學習問題，實際上就是在各個類別的條件下，用極大似然估計解決無監督學習問題。
樸素貝葉斯分類的目標是尋找“最佳”的類別
§最佳類別是指具有最大後驗概率(maximum a posteriori -MAP)的類別 cmap:

極大似然假設與貝葉斯估計的區別：
最大似然估計只考慮某個模型能產生某個給定觀察序列的概率。而未考慮該模型本身的概率。這點與貝葉斯估計區別。
Map與ML的區別：
最大後驗估計是根據經驗資料獲得對難以觀察的量的點估計。與最大似然估計類似，但是最大的不同時，最大後驗估計的融入了要估計量的先驗分佈在其中。故最大後驗估計可以看做規則化的最大似然估計。
極大後驗MAP什麼時候等於極大似然ML
不知道關於假設的任何概率，所有的hi假設擁有相同的概率，then MAP is Maximum Likelihood (hML極大似然假設），如果資料量足夠大，最大後驗概率和最大似然估計趨向於一致。
Map和樸素貝葉斯有什麼關係
If independent attribute condition is satisfied, then vMAP = vNB 如果獨立的屬性條件是滿足的vmap=vNB

、請描述極大似然估計 MLE 和最大後驗估計 MAP 之間的區別。請解釋為什麼 MLE 比 MAP更容易過擬合。
MLE：取似然函式最大時的引數值為該引數的估計值，ymle=argmax[p(x|y)]；MAP：取後驗函式（似然與先驗之積）最大時的引數值為該引數的估計值，ymap=argmax[p(x|y)p(y)]。因為MLE 只考慮訓練資料擬合程度沒有考慮先驗知識，把錯誤點也加入模型中，導致過擬合。