資訊、資訊熵、條件熵、資訊增益、資訊增益比、基尼係數、相對熵、交叉熵
參考:
http://www.cnblogs.com/fantasy01/p/4581803.html?utm_source=tuicool
http://blog.csdn.net/xbmatrix/article/details/58248347
https://www.zhihu.com/question/41252833/answer/141598211
1、資訊
引用夏農的話,資訊是用來消除隨機不確定性的東西,則某個類(xi)的資訊定義如下:
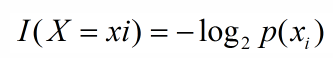
2、資訊熵
資訊熵便是資訊的期望值,可以記作:
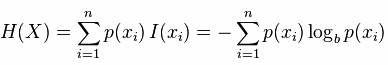
熵只依賴X的分佈,和X的取值沒有關係,熵是用來度量不確定性,當熵越大,概率說X=xi的不確定性越大,反之越小,在機器學期中分類中說,熵越大即這個類別的不確定性更大,反之越小,當隨機變數的取值為兩個時,熵隨概率的變化曲線如下圖:
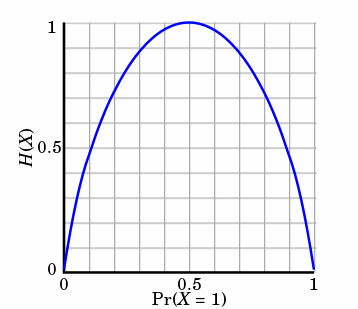
當p=0或p=1時,H(p)=0,隨機變數完全沒有不確定性,當p=0.5時,H(p)=1,此時隨機變數的不確定性最大
更特別一點,如果是個二分類系統,那麼此係統的熵為:
H(X)=-(P(c0)log2p(c0)+p(c1)log2p(c1))3. 條件熵
X給定條件下Y的條件分佈的熵對X的數學期望,在機器學習中為選定某個特徵後的熵,公式如下:
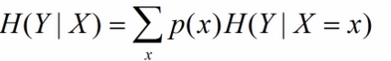
一個特徵對應著多個類別Y,因此在此的多個分類即為X的取值x。
4. 資訊增益
資訊增益在決策樹演算法中是用來選擇特徵的指標,資訊增益越大,則這個特徵的選擇性越好,在概率中定義為:待分類的集合的熵和選定某個特徵的條件熵之差(這裡只的是經驗熵或經驗條件熵,由於真正的熵並不知道,是根據樣本計算出來的),公式如下:
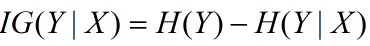
5. 資訊增益比
資訊增益的一個大問題就是偏向選擇特徵值比較多的屬性從而導致overfitting,那麼我們能想到的解決辦法自然就是對分支過多的情況進行懲罰(penalty)了。於是我們有了資訊增益比:
特徵X的熵:
特徵X的資訊增益 :
IG(X)=H(c)−H(c|X)
那麼資訊增益比為:
gr=H(c)−H(c|X)H(X)
6. Gini係數
Gini係數是一種與資訊熵類似的做特徵選擇的方式,可以用來資料的不純度。在CART(Classification and Regression Tree)演算法中利用基尼指數構造二叉決策樹(選擇基尼係數最小的特徵及其對應的特徵值)。
Gini係數的計算方式如下:
其中,D表示資料集全體樣本,pi表示每種類別出現的概率。取個極端情況,如果資料集中所有的樣本都為同一類,那麼有p0=1,Gini(D)=0,顯然此時資料的不純度最低。
7. 交叉熵、相對熵



